Bài 1 (trang 7 sgk Giải Tích 12 nâng cao): 

Xét chiều biến thiên của các hàm số sau:

a)y=2x³+3x²+1

b) y=x³-2x²+x+1

c)y=x+3/x

d) y=x-2/x

e) y=x⁴-2x²-5

Lời giải:

Hàm số y=2x³+3x²+1 xác định tren R.

Ta có: y’=6x²+6x=0=6x(x+1)

y’=0 => x=0 hoặc x=-1

Chiều biến thiên của hàm số được nêu trong bảng sau:

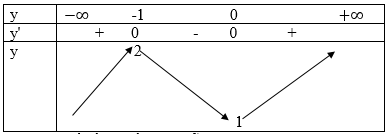
Vậy hàm số đồng biến trên mỗi khoảng (-∞; -1) và (0; +∞) nghịch biến trên (-1;0)

Tập xác định: R

Đạo hàm y’ = 3x²-4x+1

Bảng biến thiên:

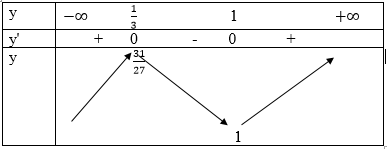
Vậy hàm số đồng biến trên mỗi khoảng (-∞;1/3) và (1; +∞) nghịch biến trên ( 1/3;1)

Tập xác định: R \{1}

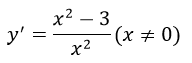
Bảng biến thiên:

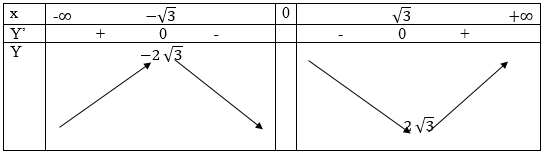
Vậy hàm số đồng biến trên mỗi khoảng (-∞,-√3) và (√3; +∞) hàm nghịch biến trên mỗi khoảng (-√3;0) và (0;√3)

d) Tập xác định: R

Vậy hàm số đồng biến trên mỗi khoảng (-∞;0) và (0; +∞)

Tập xác định: R

y’=4x³-4x=4x(x²-1)

y’=0 => x=0 hoặc x=±1

Bẳng biến thiến:

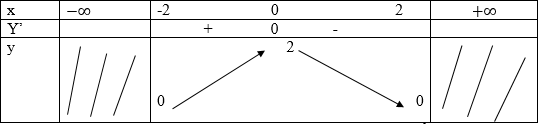
Vậy hàm số đồng biến trên [-2;0] và nghịch biến trên [0;2] (có thể trả lời: hàm số đồng biến trên (-2; 0) và nghịch biến trên (0; 2)).

Bài 2 (trang 7 sgk Giải Tích 12 nâng cao): 

Chứng minh rằng:

đồng biến trên mỗi khoảng xác định của nó.

nghịch biến trên mỗi khoảng của nó.

Lời giải:

a) Hàm số xác định trên R \ {-2}

Nên hàm số đồng biến trên mỗi khoảng (-∞; -2) và (-2 ; +∞)

Hàm số xác định trên R \ {-1}

Nên hàm số nghịch biến trên mỗi khoảng ( -∞; -1) và (-1; +∞)

Bài 3 (trang 8 sgk Giải Tích 12 nâng cao): 

Chứng minh rằng các hàm số sau đồng biến trên R.

a)f(x)=x³-6x²+17x+4=0;

b) f(x)=x³+x-cos⁡x-4

Lời giải:

Hàm số f(x)=x³-6x²+17x+4=0 xác định trên R.

Ta có f’ (x)=3x²-12x+17=3(x-2)²+5>0 ∀x ∈R.

Nên hàm số đồng biến trên R.

Hàm số f(x) xác định trên R.

Và f’ (x)=3x²+1+sin⁡x>0 ∀x ∈R (x²≥0;1+sin²⁡x≥0;3x²+1+sin⁡x=0 vô nghiệm). nên hàm số đồng biến trên R.

Bài 4 (trang 8 sgk Giải Tích 12 nâng cao):

Với giá trị nào của a, hàm số y=ax-x² nghịch biến trên R?

Lời giải:

Hàm số xác định trên R, y’=a-3x²

Cách 1. Nếu a < 0 => y’ < 0 ∀x ∈R => hàm số nghịch biến trên R.

Nếu a = 0 => y’ = -3x²≤0,∀x ∈R,y’=0 <=> x = 0

Vậy hàm số nghịch biến trên R.

Nếu a >0 thì y’=0

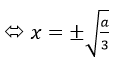
Bảng biến thiên:

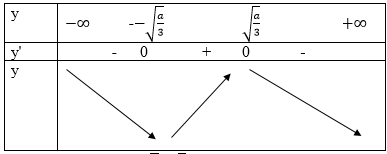
Cách 2. Hàm số nghịch biến trên R, điều kiện y’≤0,∀x ∈R,y’=0 chỉ tạo một số hữu hạn điểm.

Ta có: y’≤0 <=> a-3x²≤0 <=> 3x² ∀x ∈R

<=> a≤min⁡(3x² ),mà 3x²≥0 ∀x ∈R

Kết luận: với a≤0 thì y=ax-3x³ nghịch biến trên R.

Bài 5 (trang 8 sgk Giải Tích 12 nâng cao): 

Tìm các giá trị của tham số a để hàm số f(x) = 1/3 x³+ax²+4x+3 đồng biến trên R.

Lời giải:

f(x) xác định trên R.

f’ (x)=x²+2ax+4;Δf”=a²-4

Cách 1.

+ nếu a²-4<0 hay -2< a < 2 thì f’(x) > 0, ∀x ∈R => hàm số đồng biến trên R.

+ Nếu a²-4=0 hay a=±2

Với a = 2 thì f’(x) = (x+2)²>0 ∀x ≠ -2. Hàm số đồng biến trên R.

Với a = -2 thì f’(x) = (x-2)²>0 ∀x ≠ 2. Hàm số đồng biến trên R.

+ Nếu a²-4>0 hay a< – 2 hoặc a> 2 thì f’(x) = 0 có 2 nghiệm phân biệt x₁,x₂. Giả sử x₁<x₂, khi đó hàm số nghịch biến trên khoảng (x₁,x₂). Vậy các giá trị này của a không thõa mãn yên cầu bài toán.

Cách 2.

Hàm số đồng biến trên R khi và chỉ khi f’(x) > 0 ∀x ∈R f’(x) = 0 chỉ tại một số hữu hạn điểm.

Kết luận: hàm số đồng biến trên R khi và chỉ khi -2≤ a≤2

Comments

comments