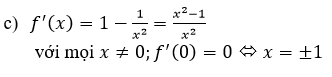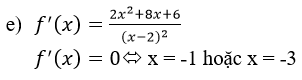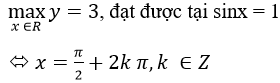Bài 16 (trang 22 sgk Giải Tích 12 nâng cao): 

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: f(x) = sin⁴x+cos⁴⁡x.

Lời giải:

Hàm số xác định trên R.

Ta có f(x) = (sin²⁡⁡x )²⁡+(cos²⁡⁡x )²⁡=(sin²⁡⁡x+cos²⁡x )²⁡-2sin²⁡x.cos²⁡x=1-1/2 sin²⁡⁡2x với x ∈R.

f(x)≤1,∀x ∈R,f(0)=0.

f(x)≥1/2,∀x ∈R (do sin²2x≤1);f(π/4)=1-1/2=1/2.

Bài 17 (trang 22 sgk Giải Tích 12 nâng cao):

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

f(x)=x²+2x-5 trên đoạn [-2; 3]

f(x)=x³/3+2x²+3x-4 trên [-4; 0]

f(x)=x+1/x trên khoảng (0; +∞)

f(x)=-x²+2x+4 trên đoạn [2; 4]

f(x)=x-1/x trên nửa khoảng (0; 2)

Lời giải:

Bảng biến thiên:

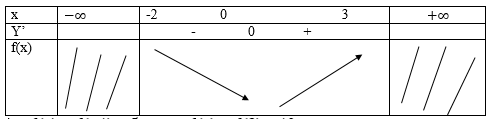
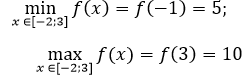
Cách 2, ta có: f(-2) = -5; f(-1) = -6; f(3) = 10

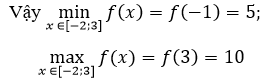
f’ (x)=x²+4x+3;f’ (x)=0 <=> x = -1 hoặc x = -3

Ta có: f(-4) = -16/3;f(-3)=-4;f(-1)=-16/3;f(0)=-4

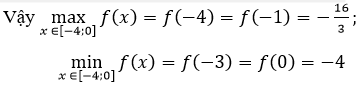
Bảng biến thiên:

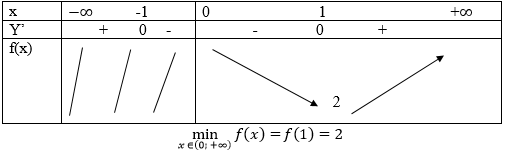
Hàm số không đạt giá trị lớn nhất trên (0; +∞)

f’ (x)=-2x+2;f'(x)=0 <=> x = 1 (loại vì x = 1 không thuộc [2;4])

Ta có: f(2)=4;f(4)=-4

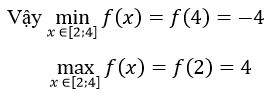
Cách 1. Bảng biến thiên:

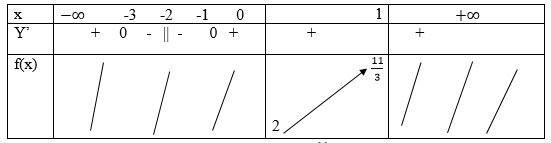
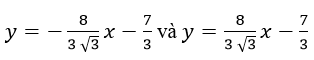
Cách 2. Vì x ∈ [0;1] nên Phương trình f’(x) = 0 vô nghiệm trên [0; 1]

Ta có: f(0) = 2; f(1) = 11/3

f(x)=x-1/x;f'(x)=1+(1/x²) >0,∀x ∈(0;2),f(x)liên tục trên (0; 2] nên f(x) đồng biến trên (0; 2]

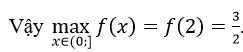
Hàm số không đạt giá trị nhỏ nhất trên nửa khoảng (0; 2].

Bài 18 (trang 22 sgk Giải Tích 12 nâng cao): 

Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) y=2 sin²⁡x+2sinx-1

b) y=cos²⁡x-sinxcosx+4

Lời giải:

Đặt t = sin x, -1≤t≤1

y=f(t)=2t²+2t-1,t ∈[-1;1]

Ta tìm giá trị lớn nhất và giá trị nhỏ nhất của y = f(t) trên [-1;1]. Đó là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên R

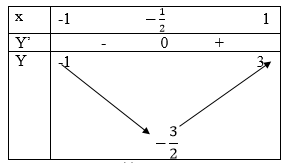
f’ (t)=4t+2,f’ (t)=0 <=> t=-1/2

Bảng biến thiên:

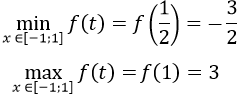
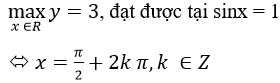
y=cos²x-sinxcosx+4=1-sin²2x-1/2 sin2x+4

=-sin²⁡2x-1/2 sin⁡2x+5

Đặt t = sin 2x, -1≤t≤1

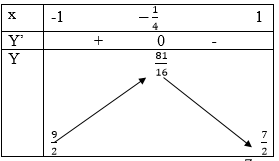
y=f(t)=-t²-1/2 t+5;f’ (t)=-2t-1/2;f’ (x)=0 <=> t=-1/4

Bảng biến thiên:

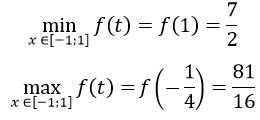
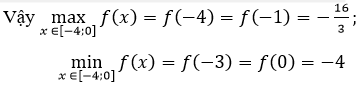
Bài 19 (trang 22 sgk Giải Tích 12 nâng cao): 

Cho tam giác đều ABC cạnh a. người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên BC, hai đỉnh P và Q theo thứ tự nằm trên hai cạnh AC và AB của tam giác. Xác định vị trị của điểm M sao cho hình chữ nhật có diện tích lớn nhất và giá trị lớn nhất đó là.

Lời giải:

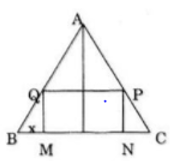
Đặt BM = x (0<x<a/2)

Ta có: MN – a – 2x; QM = BM.tan B =x √3

Diện tích hình chữ nhật MNPQ là:

S(x)=QM.MN=x √3(a-2x)

S(x)=√3(ax-2x²)

Bài toán trở thành tìm giá trị lớn nhất của S(x) trên khoảng (0; a/2)

Ta có S’ (x)=√3 (a-4x);S’ (x)=0 <=> x=a/4

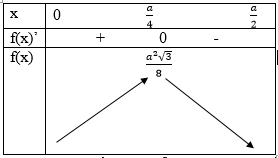
S đạt giá trị lớn nhất tại x=a/4 và giá trị lớn nhất của diện tích hình chữ nhât MNQP là:

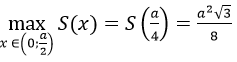
Bài 20 (trang 22 sgk Giải Tích 12 nâng cao):

Một hợp tác xã nuôi cá trong hồ. nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng:

P(n)=480-20n (gam)

Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?

Lời giải:

Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì sau một vụ, số cá trên mỗi đơn vị diện tích mặt hồ trung bình cân năng:

f(n)=n-P(n)=480n-20n² (gam)n ∈N*

Xét hàm số f(x) = 480x-20x² trên (0; +∞)

( Biến n lấy các giá trị nguyên dương được thay bằng biến số x lấy các giá trị trên khoảng (0; +∞))

f’ (x)=480-40x;f’ (x)=0 <=>x = 12

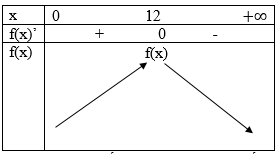
Tren (0; +∞) hàm số f(x) đạt giá trị lớn nhất tại x = 12

Suy ra trên tập hợp N* các số nguyên dương, hàm số f đạt giá trị lớn nhất tại điểm n = 12.

Vậy muốn thu hoạch được nhiều cá nhất sau một vụ thì trên mỗi đơn vị diện tích của mặt hồ phải thả 12 con cá.

Comments

comments