Bài 1 (trang 122 sgk Hình Học 12 nâng cao): Cho hình lăng trụ ABC.A’B’C’ với cạnh bên không vuông góc với mặt đáy. Gọi (α) là mặt phẳng vuông góc với các cạnh bên của hình lăng trụ và cắt chúng tại P, Q, R. Phép tịnh tiến theo vectơ AA’→ biến tam giác PQR thành tam giác P’Q’R’

a) Chứng minh rằng thể tích V của hình lăng trụ đã cho bằng thể tích hình lăng trụ PQR.P’Q’R’.

b) Chứng minh rằng V=S_PQR.AA’, trong đó S_PQR là diện tích tam giác PQR.

Lời giải:

a) Phép tính tiến theo vectơ AA’→ biến khối đa diện ABC.PQR thành khối đa diện A’B’C’.P’Q’R’ nên V_ABC.PQR=V_{A’B’C’.P’Q’R’}, suy ra: V_{ABC.A’B’C’}=V_{PQR.P’Q’R’}

b) Vì PP’ ⊥ (PQR) nên V_{PQR.P’Q’R’}=PP’.S_PQR=AA’.S_PQR. Suy ra, V_{ABC.A’B’C’}=AA’.S_PQR (đpcm)

Bài 2 (trang 122 sgk Hình Học 12 nâng cao): Cho tứ diện ABCD có thể tích V. Hãy tính thể tích của hình tứ diện có đỉnh là trọng tâm các mặt của tứ diện đã cho.

Lời giải:

Gọi G₁,G₂,G₃,G₄ lần lượt là tâm của 4 mặt tứ diện.

Gọi G là trọng tâm của tứ diện ABCD

Khi đó, theo tính chất của tứ diện thì G sẽ là tam của phép vị tự biến tứ diện ABCD thành tứ diện G₁G₂G₃G₄ với tỉ số vị tự

Bài 3 (trang 122 sgk Hình Học 12 nâng cao): Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Hãy tính thể tích của tứ diện ACBD’

Lời giải:

Ta có: V_{AA’B’D’}=V_D.ACD’=V_B.ACB’=V_{C’.D’B’A}=V/6

Mà V = V_{AA’B’D’}+V_D.ACD’+V_B.ACB’+V_{C’.D’B’A}+V_ACB’D’

Bài 4 (trang 122 sgk Hình Học 12 nâng cao): Chứng minh rằng trung điểm các cạnh của một hình tứ diện đều là các đỉnh của một hình 8 mặt đều. hãy so sánh tứ diện đều đã cho và thể tích của hình 8 mặt đều đó.

Lời giải:

 

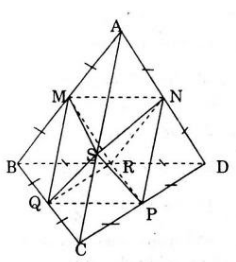
Cho tứ diện ABCD gọi M, N, P,Q, R, S lần lượt là trung điểm của 6 cạnh của tứ diện, khi đó khối đa diện MNPQRS là một hình tám mặt.

Vì MN = MR = NR = NP =NS = SP = QM = QS = MS = QP = a/2; với a là cạnh tứ diện nên MNPQRS là một hình tám mặt đều.

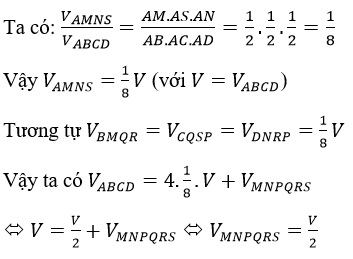
Bài 5 (trang 122 sgk Hình Học 12 nâng cao): Cho hình vuông ABCD nội tiếp đường tròn (O; R). gọi H là hình gồm các điểm của hình tròn (o; R) nhũng không gian nằm tròn hình vuông. Tính thể tích hình xoay sinh bởi hình H khi quay quanh một đường chéo của hình vuông.

Lời giải:

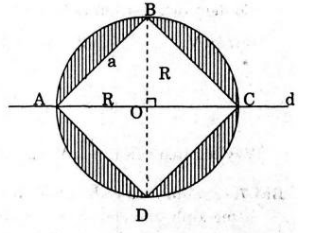
Gọi V là thể tích hình tròn xoay sinh bởi H khi quay quanh đường chéo AC, (hình vẽ). khi đó V = V₁-V₂

Trong đó V₁ là thể tích khối cầu tròn xoay tâm O, bán kính R.

Còn V₂ là thể tích khối tròn xoay sinh ra khi tam giác ABC quay quanh AC.

Bài 6 (trang 123 sgk Hình Học 12 nâng cao): Cho lục giác đều ABCDEF cạnh a.

a) Tính thể tích khối tròn xoay bởi lục giác khi quay quanh đường thẳng AD.

b) Tính thể tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường trung trực của đoạn thẳng AB.

Lời giải:

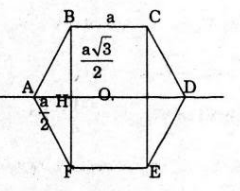
a) Vì lục giác đều ABCDEF có trục đối xứng là AD, nên thể tích khối tròn xoay cần tìm là thể tích khối tròn xoay sinh bởi hình thang cần ABCD quay quanh AD.

Khi ΔABH quay quanh AD ta được khối nón có thể tích là:

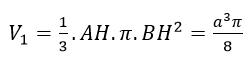
Khi BCKH quay quanh AD ta được khối trụ có thể tích là:

Vậy thể tích cần tìm là:

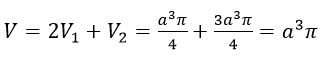
b) Do tính chất đối xứng nên thể tích cần tìm bằng 2 lần thể tích khối tròn xoay khi cho hình thang vuông AHOF quay quanh trục Δ (hình vẽ)

Khi cho AHQF quay quanh Δ ta sẽ được một khối nón cụt có đường cao

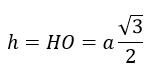
có diện tích đáy bé là

có diện tích đáy lớn là: B₂=πFO²=πa²

suy ra

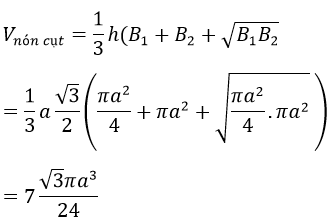
Vậy thể tích cần tìm là

Bài 7 (trang 123 sgk Hình Học 12 nâng cao): Cho hình trụ có bán kính R và đường cao R√2. Gọi AB và CD là hai đường kính thay đổi của hai đường tròn đáy mà AB vuông góc với CD.

a) Chứng minh rằng ABCD là tứ diện đều.

b) Chứng minh rằng các đường thẳng AC, AD, BC, BD luôn tiếp xúc với mọt trụ cố định (tức là khoảng cách từ các đường thẳng đó tới trục của mặt trụ bán kính mặt trụ).

Lời giải:

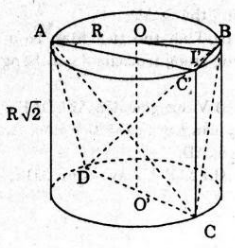
a) Vì AB ⊥ CD nên ta chứng minh được ΔDBC cân tại B, suy ra BD = BC, tương tự ta có: AC=AD=BD=BC

Trong tam giác vuông OO’C có BC²=O’B²+O’C²

Trong tam giác vuông O’OB CÓ O’B²=O’O²+OB²

Vậy BC²=O’O²+OB²+O’C²

= (R√2 )²+R²+R²=4R²

BC = 2R. vậy tứ diện ABCD có 6 cạnh bằng nhau và bằng 2R nên nó là tứ diện đều. (đpcm).

b) Kẻ đường sinh CC’ của hình trụ.

Ta có mp(C’BC) // OO’

Suy ra khoảng cách từ giữa OO’ và BC bằng khoảng cách từ OO’ đến mp(C’BC) và bằng OI (I là trung điểm BC’)

Ta tính được OI = R√2/2 (trong tam giác vuông AC’B cân tại C’)

Tương tự, khoảng cách giữa các đường thẳng AC, AD, BC, BD luôn tiếp xúc với mặt trụ có trục là đường thẳng OO’ và có bán kính là R√2/2.

Bài 8 (trang 123 sgk Hình Học 12 nâng cao): Trong không gian tọa độ OXyz cho các điểm A(1; 5; 3); B(4; 2; -5); C(5; 5; -1) và D(1; 2; 4)

a) Chứng tỏ rằng 4 điểm A, B, C, D không thẳng hàng.

b) Viết Phương trình mặt cầu (S) đi qau A, B, C, D. xác định tâm và tính bán kính mặt cầu đó.

c) Viết Phương trình mặt phẳng đi qua 3 điểm A, B, C và tìm khoảng cách từ điểm D tới mặt phẳng đó.

d) Viết Phương trình mặt phẳng vuông góc với CD và tiếp xúc với mặt cầu (S).

e) Tìm bán kính các đường tròn giao tuyến của mặt cầu (S) và các mặt phẳng tọa độ.

Lời giải:

a) Ta có [AB→,AC→ ].AD→=72 ≠ 0 nên A, B, C, D không đồng phẳng.

b) Giả sử mặt cầu (S) có Phương trình (x-a)²+(y-b)²+(z-c)²=R²

Vì mặt cầu (S) đi qua A, B, C, D nên ta có hệ:

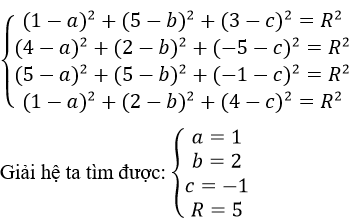
Vậy Phương trình của (S) là: (x-1)²+(y-2)²+(z+1)²=25

Tâm của (S) là I = (1; 2; -1), bán kính là R = 5.

c) Mặt phẳng ABC đi qua A(1; 5; 3) và nhận vectơ: [AB→,AC→ ]=(12; -20;12) làm vectơ pháp tuyến nên có phương trình là:

12(x-1)-20(y-5)+12(z-3)=0

<=> 3x-5y+3z+13=0

d) Mặt phẳng (α) vuông góc với CD là mặt phẳng có vectơ pháp tuyến CD→=(-4; -3;5) nên có phương trình dạng: -4x-3y+5z+D=0

vì (α) tiếp xúc với mặt cầu (S) có tâm I(1; 2; -1) và R=5

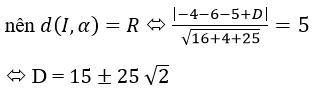
vậy có hai mặt phẳng (α) là: -4x-3y+5z+15+15√2=0 và

-4x-3y+5z+15-25√2=0

e) Bán kính của đường tròn giao tuyến của mp(P) với mặt cầu (S) là:

trong đó R là bán kính của (S), h = d(I, (P))

Nếu mp(P) là mp(Oxy) thì h = 1 => r₁=√(24)=2√6

Nếu mp(P) là mp(Oyz) thì h = 1 => r₂=√(24)=2√6

Nếu mp(P) là mp(Oxz) thì h = 2 => r₃=√(21)

Bài 9 (trang 123 sgk Hình Học 12 nâng cao): Trong không gian tọa độ Oxyz, cho đường thẳng Δ có phương trình

a) Viết phương trình hình chiếu của Δ trên các mặt phẳng tọa độ.

b) Chứng minh rằng mặt phẳng: x+5y+z+4=0 đi qua Δ.

c) Tính khoảng cách giữa đường thẳng Δ và các trục tọa độ.

d) Viết phương trình đường vuông góc chung của Δ và đường thẳng Δ’:x=y=z

e) Viết phương trình đường thẳng song song với Oz, cắt cả Δ và Δ’

Lời giải:

a) Mặt phẳng chứa Δ và vuông góc với mp(Oxy) có phương trình là:

x+2y+1=0

Vậy hình chiếu vuông góc của Δ lên mp(Oxy) có phương trình là:

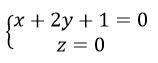
Tương tự, hình chiếu vuông góc của Δ lên mp()yz) và (Oxz) có phương trình là:

b) Δ đi qua M₀ (1; -1;0) và có vectơ pháp tuyến u→=(1;5;1) ta thấy:

suy ra Δ nằm trên mp: a+5y+z+4=0

Cách khác: ta thấy tọa độ 2 điểm M₀ (1; -1;0) và M₁ (3; -2;3) thõa mãn phương trình mp: x+5y+z+4=0 nên Δ thuộc mặt phẳng đã cho.

c) Khoảng cách giữa Δ và trục Ox được xác định như sau:

Trong đó u→=(2; -1;3) là vectơ chỉ phương của Δ

i ⃗=(1;0;0)là vectơ chỉ phương của Ox.

M₀ (1; -1;0) ∈Δ,O(0;0;0) là gốc tọa dộ.

Ta có [uX→,i→]=(0;3;1),OM₀→=(1; -1;0)

d) Đường thẳng Δ đi qua M₀ (1; -1;0) có vectơ chỉ phương u→=(2; -1;3)

Δ’ đi qua M₀‘(0;0;0) có vectơ chỉ phương u’→=(1;1;1)

Mặt phẳng (P) chứa Δ và đường thẳng vuông góc chung của Δ và Δ’ có phương trình là: 3x+9y+z+6=0.

Mặt phẳng (Q) chứa Δ’ và đường vuông góc chung của Δ và Δ’ có phương trình là: -2x+7y-5z=0

Suy ra đường vuông góc chung của Δ và Δ’ có Phương trình tổng quát là:

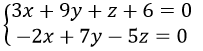
e) Đường thẳng cần tìm là giao tuyến của (α) và (β); trong đó, (α) là mặt phẳng chứa Δ và (α) song song với Oz.

(β) là mặt phẳng chứa Δ’ và (β) song song với OZ.

Phương trình của (α) là: x+2y+1=0

Phương trình của (β) là: x-y=0

Suy ra Phương trình đường thẳng cần tìm là:

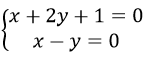
Bài 10 (trang 124 sgk Hình Học 12 nâng cao): Trong không gian tọa đọ Oxyz cho hai ddierm A(1; -1; 2), B(2; 0; 1)

a) Tìm quỹ tích các điểm M sao cho: MA²-MB²=2

b) Tìm quỹ tích các điểm N sao cho NA²+NB²=3

c) Tìm quỹ tích các ddierm cách đều hai mặt phẳng (OAB) và (Oxy)

Lời giải:

a) Giả sử M(x, y, z) là điểm thỏa mãn MA²-MB²=2 (*)

Khi đó (*) <=> (x-1)²+(y+1)²+(z-2)²-(x-2)²-y²-(z-1)²=2

<=> 2x+2y-2z-1=0 (α). Vậy quỹ tích M là mặt phẳng (α).

b) Gọi N(x, y, z) là điểm thỏa mãn NA²+NB²=3 (**)

Khi đó, (**) <=> (x-1)²+(y+1)²+(z-2)²+(x-2)²+y²+(z-1)²=3

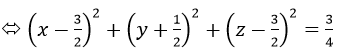
Vậy quỹ tích điểm N là mặt cầu tâm

và có bán kính R = √3/2.

c) Gọi điểm P(x, y, z) là điểm cách đều hai mặt phẳng: (OAB) và (Oxy), khi đó ta có: d(P, OAB)) = d(P, (Oxy)) (***)

Mặt phẳng (OAB) có Phương trình là: -x+3y+2z=0

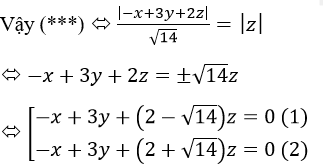
Vậy quỹ tích các điểm P thỏa mãn bài toán là hai mặt phẳng lần lượt là (1) và (2).

Bài 11 (trang 124 sgk Hình Học 12 nâng cao): Trong không gian tọa độ Oxyz, cho đường thẳng Δ có phương trình

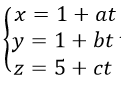
trong đó, a, b, c thay đổi sao cho c²=a²+b²

a) Chứng minh đường thẳng Δ đi qua một điểm cố định, góc giữa Δ và Oz không đổi.

b) Tìm quỹ tích điểm của Δ và mp(Oxy)

Lời giải:

a) Giả sử đường thẳng Δ đi qua điểm cố định (x₀;y₀;z₀) ta có:

Theo bài ra a²=b²+c²

Suy ra: (x₀-1)²+(y₀-1)²=a² t²+b² t²=(a²+b² ) t²=c² t²=(z₀-5)²

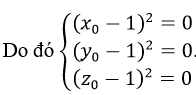
Vậy đường thẳng Δ luôn đi qua điểm (1; 1; 5) cố định.

Ta có: u_Δ→=(a,b,c);u_Oz→=(0;0;1). Do a²+b²=c²

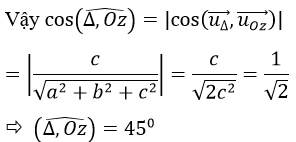
Vậy góc giữa Δ và Oz luôn bằng 45^o không đổi.

b) Gọi M(x, y, 0) là giao điểm Δ và mp(Oxy)

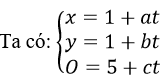
với a²+b²=c²

Suy ra (x-1)²+(y-1)²=a² t²+b² t²=(a²+b² ) t²=c² t²=5²

Vậy quỹ tích điểm M là đường tròn I(1; 1; 0) và bán kính bằng 5 trong mp(Oxy)

Bài 12 (trang 124 sgk Hình Học 12 nâng cao): Cho hình hộp chữ nhật ABCD.A’B’C’D’ với: AB=a;Bc=b;CC^’=a.

a) Tính khoảng cách từ điểm A tới mp(A’BD).

b) Tìm khoảnh cách từ điểm A’ tới đường thẳng C’D.

c) Tính khoảng cách giữa hai đường thẳng BC’ và CD’.

Lời giải:

Chọn hệ trục tọa độ Oxyz gắn vào hình hộp chữ nhật ABCD.A’B’C’D’ sao cho A’(0; 0;0); A(0; 0; c); D’(0; b; 0), B’(a; 0; 0)

Suy ra: B(a; 0; c); D(0; b; c), C(a, b, c); C’(a, b, 0)

a) Mặt phẳng (A’BD) có phương trình là: bcx+acy-abz=0

Nên khoảng cách từ A(0; 0; c) đến mp(A’BD) là:

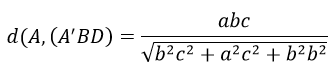
b) Khoảng cách từ A’ đến đường thẳng C’D được xác định như sau:

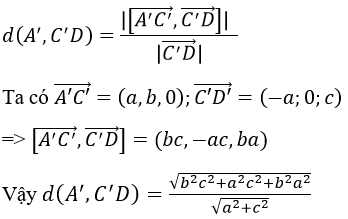
c) Khoảng cách giữa hai đường thẳng BC’ và CD’ được xác định như sau:

 

Comments

comments