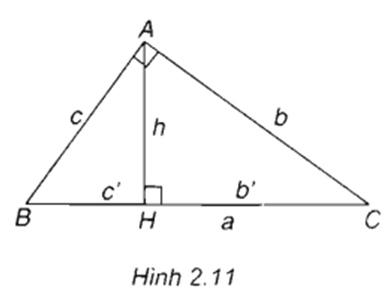
Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 46: Tam giác ABC vuông tại A có đường cao AH = h và có BC = a, CA = b, AB = c. Gọi BH = c’ và CH = b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:

a² = b² + (…..)

b² = a x (…..)

c² = a x (…..)

h² = b’ x (…..)

ah = b x (…..)

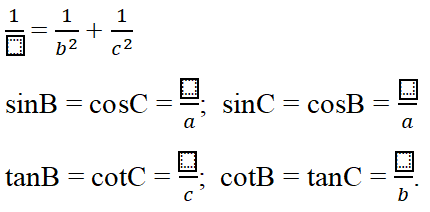
Lời giải

a² = b² + c²

b² = a x b’

c² = a x c’

h² = b’ x c’

ah = b x c

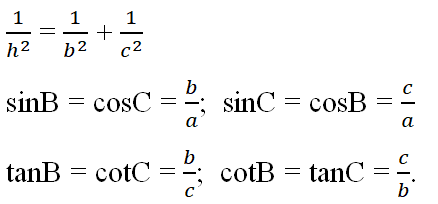
Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 48: Khi ABC là tam giác vuông, định lý côsin trở thành định lý quen thuộc nào ?

Lời giải

Khi ABC là tam giác vuông, định lý côsin trở thành định lý Py- ta – go.

Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 49: Cho tam giác ABC có a = 7cm, b = 8cm, c = 6cm. Hãy tính độ dài đường trung tuyến m_a của tam giác ABC đã cho.

Lời giải

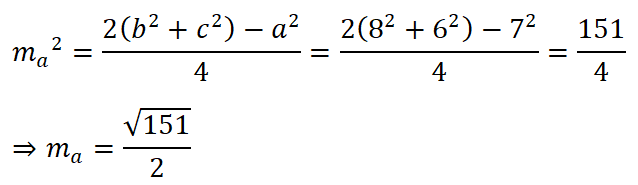
Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 50: Cho tam giác ABC vuông ở A nội tiếp trong đường tròn bán kính R và có BC = a, CA = b, AB = c.

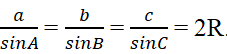
Chứng minh hệ thức:

Lời giải

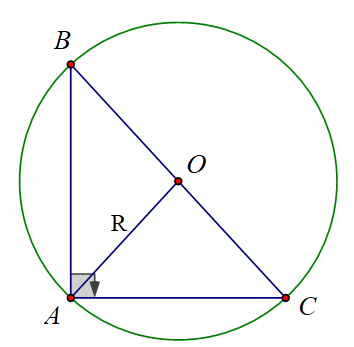
Do tam giác ABC vuông tại A nên trung điểm O của BC là tâm đường tròn ngoại tiếp tam giác ABC ⇒ BC = a = 2R

Ta có:

Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 52: Cho tam giác đều ABC có cạnh bằng a. Hãy tính bán kính đường tròn ngoại tiếp tam giác đó.

Lời giải

Theo định lí sin ta có:

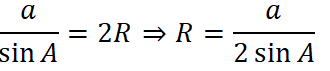
Tam giác ABC đều nên A = 60^o ⇒ sin ⁡A = √3/2

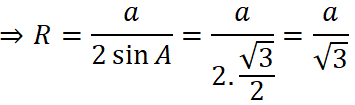
Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 53: Hãy viết các công thức tính diện tích tam giác theo một cạnh và đường cao tương ứng.

Lời giải

S = 1/2 a.h_a = 1/2 b.h_b = 1/2 c.h_c

Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 54: Dựa vào công thức (1) và định lý sin, hãy chứng minh S = abc/4R.

Lời giải

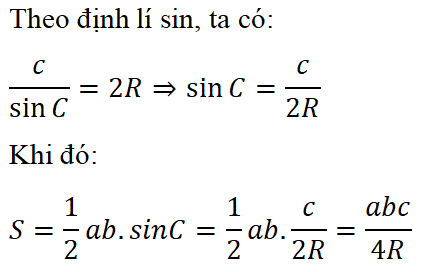
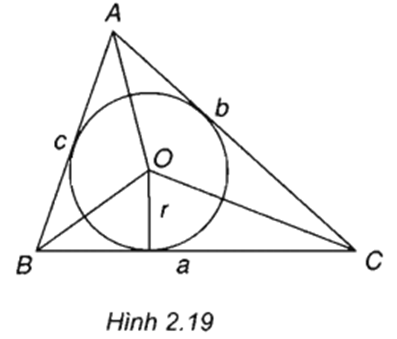
Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 54: Chứng minh công thức S = pr (h.2.19).

Lời giải

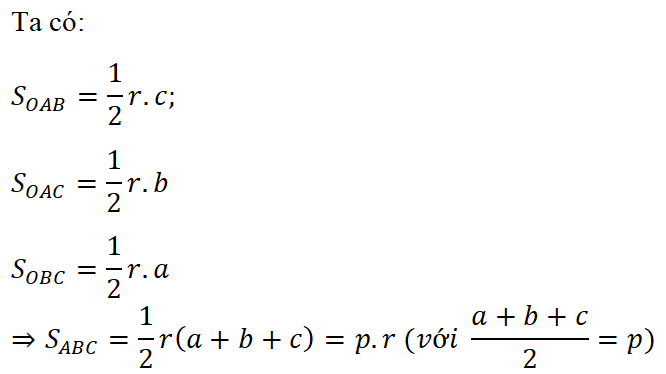
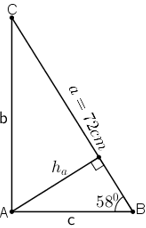
Bài 1 (trang 59 SGK Hình học 10): Cho tam giác ABC vuông tại A, B̂ = 58^o và cạnh a = 72cm. Tính Ĉ, cạnh b và đường cao h_a.

Lời giải:

+ Ĉ + B̂ = 90º ⇒ Ĉ = 90º – B̂ = 90º – 58º = 32º

+ b = a.sinB = 72 . sin 58º ≈ 61,06 cm

+ c = a . cos B = 72 . cos 58º ≈ 38,15cm

+ h_a = c . sin B = 38,15 . sin 58º = 32,36 cm.

Kiến thức áp dụng

Trong tam giác ABC vuông tại A có AB = c, BC = a, CA = b thì:

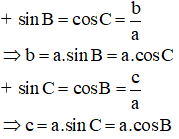
Bài 2 (trang 59 SGK Hình học 10): Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc Â, B̂, Ĉ.

Lời giải:

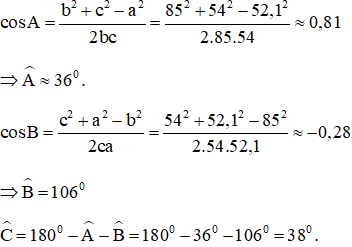
Kiến thức áp dụng

Tam giác ABC có AB = c, BC = a, CA = b thì:

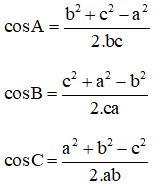
Bài 3 (trang 59 SGK Hình học 10): Cho tam giác ABC có Â = 120^o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.

Lời giải:

+ a² = b² + c² – 2.bc.cosA = 8² + 5² – 2.5.8.cos120º = 129

⇒ a = √129 cm

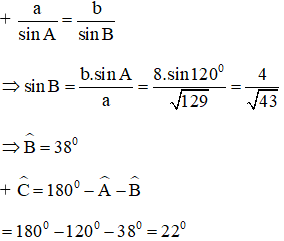
Kiến thức áp dụng

Trong tam giác ABC có AB = c, BC = a, CA = b có:

+ a² = b² + c² – 2.bc.cos A

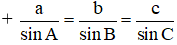
Bài 4 (trang 59 SGK Hình học 10): Tính diện tích S của tam giác có số đo các cạnh lần lượt là 7, 9 và 12.

Lời giải:

Nửa chu vi của tam giác: p = (7 + 9 + 12)/2 = 14.

Áp dụng công thức Hê–rông ta có:

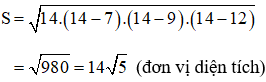
Kiến thức áp dụng

Công thức Hê–rông tính diện tích:

Tam giác có ba cạnh lần lượt là a, b, c, nửa chu vi p = (a + b + c) / 2 thì diện tích bằng:

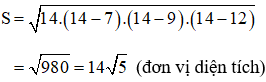
Bài 5 (trang 59 SGK Hình học 10): Cho tam giác ABC có Â = 120^o. Tính cạnh BC, cho biết cạnh AC = m và cạnh AB = n.

Lời giải:

Áp dụng định lý côsin ta có:

BC² = AB² + AC² – 2.AB.AC.cos A

= m² + n² – 2.m.n.cos120º

= m² + n² + mn.

⇒ BC = √( m² + n² + mn).

Kiến thức áp dụng

Định lý côsin: Tam giác ABC có:

AB² = AC² + BC² – 2.AC.BC.cosC

AC² = BC² + BA² – 2.BC.BA.cosB

BC² = AB² + AC² – 2.AB.AC.cosA.

Bài 6 (trang 59 SGK Hình học 10): Tam giác ABC có các cạnh a = 8cm, b = 10cm và c = 13cm.

a) Tam giác đó có góc tù không?

b) Tính độ dài trung tuyến MA của tam giác ABC đó.

Lời giải:

a) Ta có:

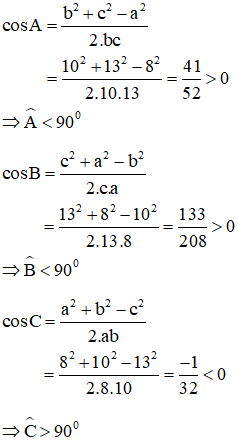
Vậy tam giác ABC có góc C tù.

b) Ta có:

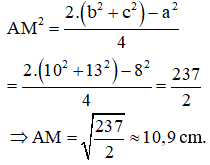
Kiến thức áp dụng

+ Định lý Côsin: Trong tam giác ABC có AB = c, BC = a, CA = b ta có:

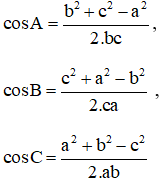
+ Công thức tính độ dài đường trung tuyến:

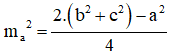
Bài 7 (trang 59 SGK Hình học 10): Tính góc lớn nhất của tam giác ABC biết:

a) Các cạnh a = 3cm, b = 4cm và c = 6cm;

b) Các cạnh a = 40cm, b = 13cm, c = 37cm.

Lời giải:

Nhận xét: Trong một tam giác, góc đối diện với cạnh lớn nhất là góc lớn nhất.

a) Cạnh c = 6cm lớn nhất nên góc lớn nhất là góc C:

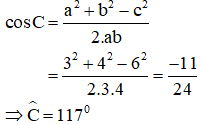
Vậy góc lớn nhất là 117º.

b) Cạnh a = 40cm lớn nhất suy ra góc lớn nhất là góc A:

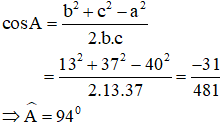
Vậy góc lớn nhất bằng 94º

Comments

comments