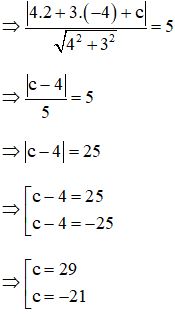Trả lời câu hỏi Toán 10 Hình học Bài 2 trang 82: Cho hai điểm A(3; -4) và B(-3; 4).

Viết phương trình đường tròn (C) nhận AB là đường kính.

Lời giải

Gọi I là đường tròn nhận AB là đường kính

⇒ I là trung điểm của AB ⇒ I (0; 0)

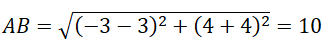
⇒ R = AB/2 = 5

Phương trình đường tròn (C) nhận AB là đường kính là:

x² + y² = 25

Trả lời câu hỏi Toán 10 Hình học Bài 2 trang 82: Hãy cho biết phương trình nào trong các phương trình sau đây là phương trình đường tròn:

2x² + y² – 8x + 2y – 1 = 0;

x² + y² + 2x – 4y – 4 = 0;

x² + y² – 2x – 6y + 20 = 0;

x² + y² + 6x + 2y + 10 = 0.

Lời giải

+ 2x² + y² – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x² khác hệ số của y².

+ Phương trình x² + y² + 2x – 4y – 4 = 0 có :

a = –1; b = 2; c = –4 ⇒ a² + b² – c = 9 > 0

⇒ phương trình trên là phương trình đường tròn.

+ Phương trình x² + y² – 2x – 6y + 20 = 0 có :

a = 1; b = 3; c = 20 ⇒ a² + b² – c = –10 < 0

⇒ phương trình trên không là phương trình đường tròn.

+ Phương trình x² + y² + 6x + 2y + 10 = 0 có :

a = –3; b = –1; c = 10 ⇒ a² + b² – c = 0 = 0

⇒ phương trình trên không là phương trình đường tròn.

Bài 1 (trang 83 SGK Hình học 10): Tìm tâm và bán kính của các đường tròn sau:

a, x² + y²– 2x – 2y – 2 = 0

b, 16x² + 16y² + 16x – 8y -11 = 0

c, x² + y² – 4x + 6y – 3 = 0

Lời giải

Cách 1 : Xác định các hệ số a, b, c.

a) x² + y² – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2

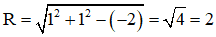
⇒ tâm I (1; 1) và bán kính

b) 16x² + 16y² + 16x – 8y –11 = 0

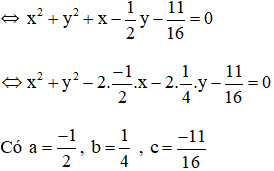
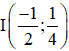
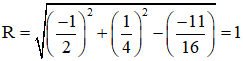
⇒ Đường tròn có tâm , bán kính

c) x² + y² – 4x + 6y – 3 = 0

⇔ x² + y² – 2.2x – 2.(-3).x – 3 = 0

có hệ số a = 2, b = -3,c = -3

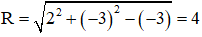
⇒ Đường tròn có tâm I(2 ; –3), bán kính

Cách 2 : Đưa về phương trình chính tắc :

a) x² + y² – 2x – 2y – 2 = 0

⇔ (x² – 2x + 1) + (y² – 2y +1) = 4

⇔(x-1)² + (y-1)² = 4

Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.

b) 16x² + 16y² + 16x – 8y – 11 = 0

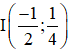
Vậy đường tròn có tâm và bán kính R = 1.

c) x² + y² – 4x + 6y -3 = 0

⇔ (x² – 4x + 4) + (y² + 6y + 9) = 4 + 9 + 3

⇔ (x – 2)² + (y + 3)² = 16

Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.

Kiến thức áp dụng

+ Phương trình chính tắc của đường tròn tâm I(a ; b) và bán kính bằng R là :

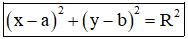
+ Ngoài ra phương trình đường tròn còn được viết dưới dạng : x² + y² – 2ax – 2by + c = 0

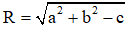
Trong đó I(a ; b) là tâm đường tròn và bán kính

Bài 2 (trang 83 SGK Hình học 10): Lập phương trình đường tròn (C) trong các trường hợp sau:

a, (C) có tâm I(-2; 3) và đi qua M(2; -3);

b, (C) có tâm I(-1; 2) và tiếp cúc với đường thẳng x – 2y +7 =0

c, (C) có đường kính AB với A = (1; 1) và B = (7; 5).

Lời giải

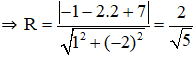
a) (C) có tâm I và đi qua M nên bán kính R = IM

Vậy đường tròn (C) : (x + 2)² + (y – 3)² = 52.

b) (C) tiếp xúc với (Δ) : x – 2y + 7 = 0

⇒ d(I; Δ) = R

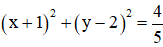
Vậy đường tròn (C) :

c) (C) có đường kính AB nên (C) có :

+ tâm I là trung điểm của AB

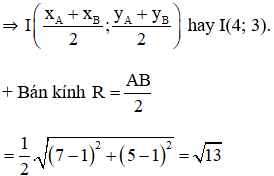
Vậy đường tròn (C) : (x – 4)² + (y – 3)² = 13.

Kiến thức áp dụng

Để viết phương trình đường tròn ta cần xác định :

+ Tâm I(a ; b)

+ Bán kính R.

Khi đó phương trình đường tròn (x – a)² + (y – b)² = R².

Bài 3 (trang 84 SGK Hình học 10): Lập phương trình đường tròn đi qua ba điểm:

a, A(1; 2), B(5; 2), C(1; -3)

b, M(-2; 4), N(5; 5), P(6; -2)

Lời giải

Gọi phương trình đường tròn (C) là: x² + y² – 2ax – 2by + c = 0.

a) A(1; 2) ∈ (C) ⇔ 1² + 2² – 2.a.1 – 2.b.2 + c = 0 ⇔ 2a + 4b – c = 5 (1)

B(5; 2) ∈ (C) ⇔ 5² + 2² – 2.5.x – 2.2.y + c = 0 ⇔ 10x + 4y – c = 29 (2)

C(1; –3) ∈ (C) ⇔ 1² + (–3)² – 2.a.1 – 2.b.(–3) + c = 0 ⇔ 2a – 6b – c = 10 (3)

Từ (1), (2) và (3) ta có hệ phương trình :

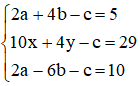
Giải hệ phương trình trên ta được nghiệm a = 3, b = –1/2, c = –1.

Vậy đường tròn đi qua ba điểm A, B, C là : x² + y² – 6x + y – 1 = 0.

b)

M(–2 ; 4) ∈ (C) ⇔ (–2)² + 4² – 2.a.(–2) – 2.b.4 + c = 0 ⇔ 4a – 8b + c = –20 (1)

N(5; 5) ∈ (C) ⇔ 5² + 5² – 2.a.5 – 2.b.5 + c = 0 ⇔ 10a + 10b – c = 50 (2)

P(6; –2) ∈ (C) ⇔ 6² + (–2)² – 2.a.6 – 2.b.(–2) + c = 0 ⇔ 12a – 4b – c = 40 (3)

Từ (1), (2) và (3) ta có hệ phương trình:

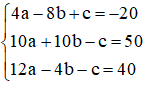
Giải hệ phương trình trên ta được nghiệm a = 2, b = 1, c = –20.

Vậy đường tròn đi qua ba điểm M, N, P là : x² + y² – 4x – 2y – 20 = 0.

Kiến thức áp dụng

Đường tròn (C) có tâm I(a ; b) và bán kính R có hai cách viết phương trình :

(C) : (x – a)² + (y – b)² = 0

hoặc (C) : x² + y² – 2ax – 2by + c = 0 (Với c = a² + b² – R²).

Bài 4 (trang 84 SGK Hình học 10): Lập phương trình đường tròn tiếp xúc với hai trục tọa độ Ox, Oy và qua điểm M(2; 1).

Lời giải

Gọi đường tròn cần tìm là (C) có tâm I(a ; b) và bán kính bằng R.

(C) tiếp xúc với Ox ⇒ R = d(I ; Ox) = |b|

(C) tiếp xúc với Oy ⇒ R = d(I ; Oy) = |a|

⇒ |a| = |b|

⇒ a = b hoặc a = –b.

+ TH1: Xét a = b thì I(a; a), R = |a|

Ta có: M ∈ (C) ⇒ IM = R ⇒ IM² = R²

⇒ (2 – a)² + (1 – a)² = a²

⇔ a² – 6a + 5 = 0

⇔ a = 1 hoặc a = 5.

* a = 1 ⇒ I(1; 1) và R = 1.

Ta có phương trình đường tròn (C): (x – 1)² + (y – 1)² = 1.

* a = 5 ⇒ I(5; 5), R = 5.

Ta có phương trình đường tròn (C) : (x – 5)² + (y – 5)² = 25.

+ TH2: Xét a = –b thì I(a; –a), R = |a|

Ta có: M ∈ (C) ⇒ IM = R ⇒ IM² = R²

⇒ (2 – a)² + (1 + a)² = a²

⇔ a² – 2a + 5 = 0 (Phương trình vô nghiệm)

Vậy có hai đường tròn thỏa mãn là: (C): (x – 1)² + (y – 1)² = 1 hoặc (C) : (x – 5)² + (y – 5)² = 25.

Kiến thức áp dụng

+ Đường tròn (C) có tâm I(a ; b) và bán kính R có hai cách viết phương trình :

(C) : (x – a)² + (y – b)² = 0

hoặc (C) : x² + y² – 2ax – 2by + c = 0 (Với c = a² + b² – R²).

+ Đường tròn (C) có tâm I, bán kính R tiếp xúc với đường thẳng Δ ⇔ d(I; Δ) = R.

Bài 5 (trang 84 SGK Hình học 10): Lập phương trình của đường tròn tiếp xúc với các trục tọa độ và có tâm nằm trên đường thẳng 4x – 2y – 8 = 0

Lời giải

Kiến thức áp dụng

+ Đường tròn (C) có tâm I(a ; b) và bán kính R có hai cách viết phương trình :

(C) : (x – a)² + (y – b)² = 0

hoặc (C) : x² + y² – 2ax – 2by + c = 0 (Với c = a² + b² – R²).

+ Đường tròn (C) có tâm I, bán kính R tiếp xúc với đường thẳng Δ ⇔ d(I; Δ) = R.

Bài 6 (trang 84 SGK Hình học 10): Cho đường tròn C có phương trình: x² + y² – 4x + 8y – 5 = 0

a, Tìm tọa độ tâm và bán kính của (C)

b, Viết phương trình tiếp tuyến với (C) đi qua điểm A(-1; 0)

c, Viết phương trình tiếp tuyến với (C) vuông góc với đường thẳng: 3x – 4y + 5 = 0.

Lời giải

a) x² + y² – 4x + 8y – 5 = 0

⇔ (x² – 4x + 4) + (y² + 8y + 16) = 25

⇔ (x – 2)² + (y + 4)² = 25.

Vậy (C) có tâm I(2 ; –4), bán kính R = 5.

b) Thay tọa độ điểm A vào phương trình đường tròn ta thấy:

(–1 – 2)² + (0 + 4)² = 3² + 4² = 2⁵ = R²

⇒ A thuộc đường tròn (C)

⇒ tiếp tuyến (d’) cần tìm tiếp xúc với (C) tại A

⇒ (d’) là đường thẳng đi qua A và vuông góc với IA

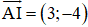
⇒ (d’) nhận là một vtpt và đi qua A(–1; 0)

⇒ phương trình (d’): 3x – 4y + 3 = 0.

c) Gọi tiếp tuyến vuông góc với (d) : 3x – 4y + 5 = 0 cần tìm là (Δ).

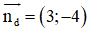
(d) có là một vtpt

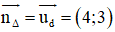
(Δ) ⊥ (d) ⇒ (Δ) nhận là một vtpt

⇒ (Δ): 4x + 3y + c = 0.

(C) tiếp xúc với (Δ) ⇒ d(I; Δ) = R

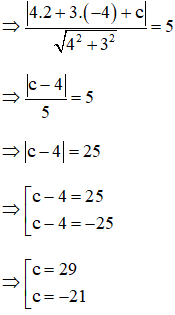
Vậy (Δ) : 4x + 3y + 29 = 0 hoặc 4x + 3y – 21 = 0.

Comments

comments