Bài 1 (trang 63 sgk Hình Học 12 nâng cao):

Cho mp (P) và điểm A không thuộc mặt phẳng (P). chứng minh rằng mọi mặt cầu đi qua A có tâm nằm trên (P) luôn luôn đi qua hai điểm cố định.

Lời giải:

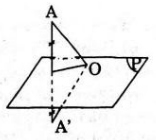
Giả sử S là mặt cầu đi qua A và có tâm O ∈ (P). (hình vẽ bên). Gọi A’ là điểm đối xứng với A qua (P) thì OA’ = OA nên mặt cầu S cũng đi qua A’.

Vậy các mặt cầu S đi qua hai điểm cố định A và A’.

Bài 2 (trang 63 sgk Hình Học 12 nâng cao):

Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABC, biết

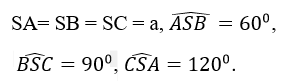
Lời giải:

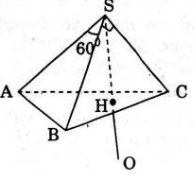
Theo (gt) => AB = a, BC = a √2 và AC = a √3

Vậy ΔABC vuông tại B.

Gọi SH là đường cao của hình chóp thì do SA = SB = SC nên HA = HB = HC, do đó H là trung điểm của AC. Gọi O là điểm đối xứng với điểm S qua điểm H.

Khi đó OS = OA = OC = OB = a. suy ra mặt cầu ngoại tiếp hình chóp có tâm O và bán kính R = a.

Bài 3 (trang 63 sgk Hình Học 12 nâng cao):

Cho hai đường tròn (O, r) và (o’, r’) cắt nhau tại hai điểm A, B và lần lượt nằm trên hai mặt phẳng phân biệt (P) và (P’).

a) Chứng minh rằng có mặt cầu (S) đi qua đường tròn đó

b) Tính bán kính của R của mặt cầu (S) khi r = 5, r’ = √10, AB = 6, OO’ = √21

Lời giải:

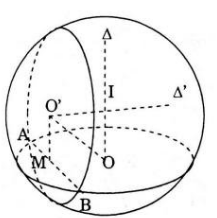
a) Gọi M là trung điểm của AB thì OM ⊥AB,O’ M⊥AB. Do (P) và (P’) phân biệt nên ba điểm O, M, O’ không thẳng hàng.

Từ đó AB ⊥ mặt phẳng (OMO’).

Gọi Δ và Δ’ lần lượt là trung trực của đường tròn (O, r) và (O’, r’) thì Δ và Δ’ cung vuông góc với AB.

Từ đó suy ra Δ và Δ’ cùng nằm trong mặt phẳng (OMO’). Δvà Δ’ cắt nhau tại điểm I. Khi đấy mặt cầu (C ) có tâm I và bán kính R = IB là mặt cầu cần tìm.

b)Ta có:

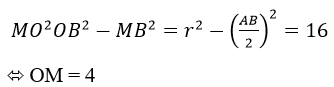
Tương tự: O’M = 1

Xét ΔOMO’ ta có:

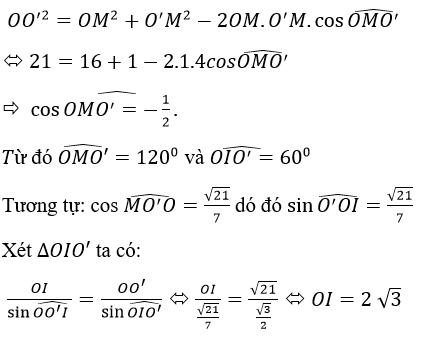
Như vậy R²=IB²+IO²=25+12=37 tức R = √37

Vậy R=√37

Bài 4 (trang 63 sgk Hình Học 12 nâng cao):

Cho một hình nón H sinh bởi một tam giác đều cạnh a khi quay quanh một đường cao.

a) Mổ mặt cầu có diện tích bằng diện tích toàn phần của hình nó H thì có bán kính bằng bao nhiêu?

b) Một khối cầu có thể tích bằng thể tích của khối nón H thì có bán kính bằng bao nhiêu?

Lời giải:

Theo gt hình nón H có bán kính đáy r=a/2, có chiều cao h=a√3/2 và có đường sinh l=a. vậy nó có diện tích toàn phần là S₁ và V thể tích

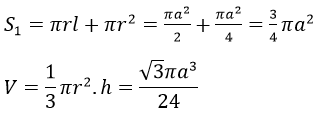
a) Nếu mặt cầu có bán kính R thì có diện tích là S₂=4 πR²

Theo bài ra

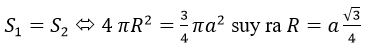
b) Nếu mặt cầu bán kính R thì có thể tích V của hình nón thì

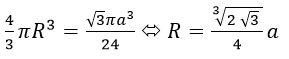
Bài 5 (trang 63 sgk Hình Học 12 nâng cao):

Cho tam giác vuông ABC vuông tạo A, AB = c, AC = b, gọi V_1,V_2,V_3 là thể tích các khối tròn xoay sinh bởi tam giác đó (kể cả các điểm trong) khi lần lượt quay quanh AB, AC, BC.

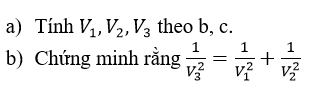
Lời giải:

a) Khi quay tam giác ABC quanh AB ta được khối nón có đường cao c và bán kính đáy b, nên nó có thể tích

Khi quay tam giác ABC quanh AC ta được khối nón có đường cao bvà bán kính đáy c, nên nó có thể tích

 

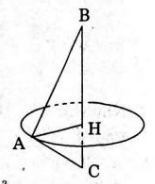
Gọi AH là đường cao của tam giác ABC. Khi quay tam giác ABC quanh BC (hình vẽ) ta được khối tròn xoay hợp thành của hai khối nón sinh ra bởi tam giác ABH và ACH khi quay quanh BC.

Vì vậy:

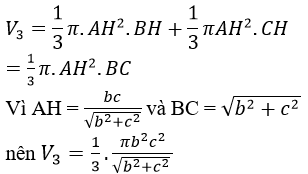
b) Ta có:

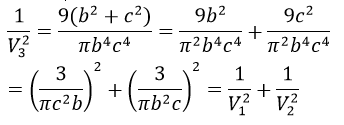
Bài 6 (trang 63 sgk Hình Học 12 nâng cao):

Một hình thang cân ABCD có dạng đáy AB = 2a, DC = 4a. Cạnh bên AD = BC =3a. cho hình thang đó (kể cả điểm trong) quay quanh trục đối xứng của nó. Hãy tính thể tích và diện tích toàn phần của khối tròn xoay được tạo thành.

Lời giải:

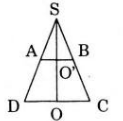
Gọi S là giao điểm của hai cạnh bên AD và BC của hình thang (hình vẽ bên). Đường cao SO của tam giác cân SCD là trục đối xứng của hình thang dó đó SO cắt AB tại trung điểm O’ của AB.

Khi quay quanh SO, tam giác SCD sinh khối nón H₁ có thể tích V₁ tam giác SAB sinh ra khối nón H₂ có thể tích V₂ còn hình thang ABCD sinh ra một khối tròn xoay H có thể tích V = V₁-V₂

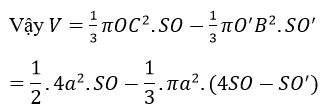
Chú ý rằng AB là đường trung bình của tam giác SCD nên SB = 3a và do đó:

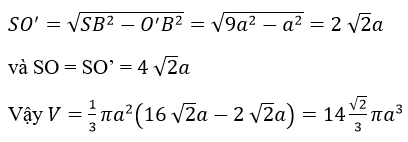
Gọi S₁,S₂ lần lượt là diện tích xung quanh của khối nón H₁,H₂ thì diện tích xung quanh của khối tròn xoay H là S_xq=S₁-S₂=π.OC.SC-PI O’ B.SB=9 πa²

=> Diện tích toàn phần S_TP=9 πa²+πa²+4 πa²=14 πa²

Comments

comments