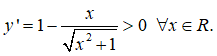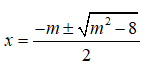Câu 7: Hàm số:

đồng biến trên khoảng nào?

A. R    B. (-∞; 0)     C. (-1; 0)    D. (0; +∞)

Câu 8: Cho hàm số y = x³ – x² + (m-1)x + m. Tìm điều kiện của tham số m để hàm số đồng biến trên R

A. m ≤ 2     B. m > 2     C. m ≥ 2    D. m <2

Câu 9: Cho hàm số

Tìm giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1).

A. m < 2√2    B. m ≥ -2√2     C. m = 2√2     D. -2√2 ≤ m 2√2

Câu 10: Tìm tất cả các giá trị của tham số m sao cho hàm số

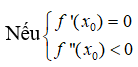
A. 1 < m < 5    B. m ≥ 5     C. m < -1 hoặc m > 5     D. m > 5

Câu 11: 11. Cho hàm số y = x³ + 3x² + mx + 1 – 2m. Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.

A. m =0     B. m = 1/4     C. 9/4     D. Không tồn tại

Hướng dẫn giải và Đáp án

7-A

8-C

9-C

10-D

11-D

Câu 7:

Hàm số đồng biến trên R

Câu 8:

y’ = x² – 2x + (m -1). Hàm số đồng biến trên R

<=> y’ > 0 ∀x ∈ R <=> Δ’ ≥ 0; Δ’ = -m + 2 ≥ 0 <=> m > 2

Câu 9:

Ta có y’ = -x² – mx – 2 . Hàm số nghịch biến trên khoảng (-∞; – 1) nếu y’ = x² – mx – 2 ≤ 0 trên khoảng (-∞; -1)

Cách 1. Dùng định lí dấu của tam thức bậc hai. Ta có Δ = m² – 8

TH1: -2√2 ≤ m ≤ 2√2 => Δ ≤ 0. Hàm số nghịch biến trên R

TH2:

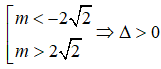
y’ = 0. có hai nghiệm phân biệt là

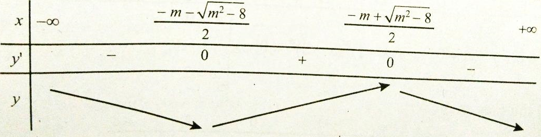
Từ TH1 và TH2, ta có m ≤ 2√2

Cách 2. Dùng phương pháp biến thiên hàm số

Ta có

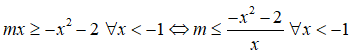
Từ đó suy ra

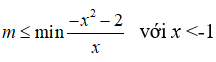
Do đó m ≤ 2√2

Vậy giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1) là m = 2√2

Câu 10:

Ta có

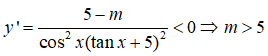
Câu 11:

y’ = 3x² + 6x + m. Hàm số đồng biến nếu y’ ≥ 0. Ta có Δ’ = 9 – 3m

TH1: m ≥ 3 => Δ’ ≤ 0 .

Hàm số đồng biến trên R. Do đó m ≥ 3 không thỏa mãn yêu cầu đề bài

TH2: m < 3 => Δ’ > 0 .

y’ có hai nghiệm phân biệt là

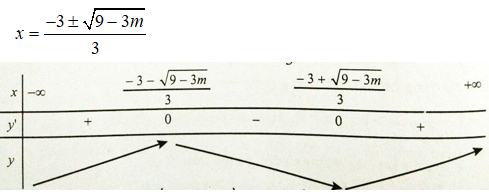
Từ bảng biến thiên, ta thấy không tồn tại m để hàm số đồng biến trên đoạn có độ dài bằng 1.

Từ TH1 và TH2, không tồn tại m thỏa mãn.

Comments

comments