Bài 1 (trang 112 sgk Hình Học 12 nâng cao):
Cho ba điểm M(2; 0; 0), N(0; -3; 0), P(0; 0; 4). Nếu MNPQ là hình bình hành thì tọa độ Q là:
A. (-2; -3; 4) B. (3; 4; 2)
C. (2; 3; 4) D. (-2; -3; -4)
Lời giải:
Vì MNPQ là hình bình hành nên MN→=PQ→
Mà NM→=(2;3;0), PQ→=(xQ;yQ;zQ-4)
Suy r xQ=2;yQ=3;zQ=4.
Vậy ta chọn C.
Bài 2 (trang 112 sgk Hình Học 12 nâng cao):
Cho ba điểm A(1, 2, 0). B(1, 0, -1); C(0; -1; 2). Tam giác ABC là:
A. Tam giác cân đỉnh A B. Tam giác vuông đỉnh A.
C. Tam giác đều D. Không phải như A, B, C.
Lời giải:
Ta có AB = √5;BC=√11,AC=√14
Vậy A, B, C không thể là đỉnh của tam giác cân hay tam giác vuông, hay tam giác đều.
Vậy ta chọn D.
Bài 3 (trang 112 sgk Hình Học 12 nâng cao):
Cho tam giác ABC có A = (1; 0; 1); B = (0; 2; 3); C = (2; 1; 0). Độ dài đường cao tam giác kẻ từ C là:
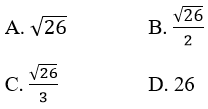
Lời giải:
Ta có độ dài đường cao kẻ từ C là khoẳng cách từ C đến đường thẳng AB và được tính theo công thức:
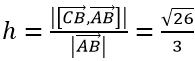
Vậy ta chọn C.
Bài 4 (trang 112 sgk Hình Học 12 nâng cao):
Ba đỉnh của một hình bình hành có tọa độ là (1, 1, 1), (2, 3, 4), (6, 5, 2). Diện tích của hình bình hành đó là:
A. 2√83 B. √83 C. 83 D. √83/2
Lời giải:
Gọi A(1; 1; 1), B(2; 3; 4); C(6; 5; 2) và D(7; 7; 5). Diện tích hình bình hành ABCD là:
S=|[AB→,AC→]| (vì AB→=CD→nên AB và AC là 2 cạnh kề nhau của hình bình hành).
Vậy S = √332=2√83, nên ta chọn A
Bài 5 (trang 112 sgk Hình Học 12 nâng cao):
Cho A(1; 0; 0); B(0; 1; 0); C(-4; -2; 0) và D(-2; 1; -1). Thể tích của tứ diện ABCD là:
A. 1 B. 2 C. 1/3 D. 1/2
Lời giải:
Thể tích tứ diện ABCD được tính theo công thức:
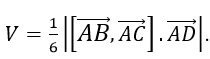
Ta tính được [AB→,AC→ ]=(1;1;1) nên V=1/2, nên chọn D
Bài 6 (trang 112 sgk Hình Học 12 nâng cao):
Cho A(-1; -2; 4); B(-4; -2; 0), C(3; -2; 1) và D(1; 1; 1). Độ dài dường cao của tứ diện ABCD kẻ từ đỉnh D là:
A. 3 B. 1 C. 2 D.1/2
Lời giải:
Độ dài dường cao của tứ diện kẻ từ đỉnh D được xác định như sau:
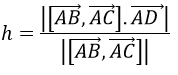
ta có [AB→,AC→ ]=(0; -25;0),AD→=(2;3; -3)
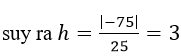
Vậy chọn (A)
Bài 7 (trang 112 sgk Hình Học 12 nâng cao):
Cho bốn điểm A(1; 1; 1); B(1; 2; 1); C(1; 1; 2) và D(2; 2; 1). Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ.
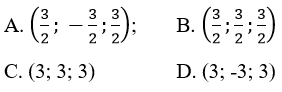
Lời giải:
I(x, y, z) là tâm mặt cầu ngoại tiếp tứ diện ABCD khi
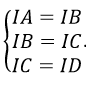
Giải hệ ta được
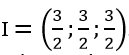
Vậy chọn B.
Bài 8 (trang 113 sgk Hình Học 12 nâng cao):
Bán kính mặt cầu tâm I(3; 3; -4) tiếp xúc với trục Oy bằng:
A. 5 B. 4 C. √5 D. 5/2
Lời giải:
Nếu mặt cầu tâm I(3; 3; -4) tiếp xúc với trục Oy thì bán kính là khoảng cách từ I đến Oy bằng:
![]()
Vậy chọn A.
Bài 9 (trang 113 sgk Hình Học 12 nâng cao):
Mặt cầu tâm I(2; 1; -1) tiếp xúc với mặt phẳng tọa độ (Oyz) có Phương trình là:
A. (x-2)2+(y-1)2+(z+1)2=4
B. (x-2)2+(y-1)2+(z+1)2=1
C. (x+2)2+(y-1)2+(z-1)2=4
D. (x+2)2+(y-1)2+(z+1)2=2
Lời giải:
Nếu mặt cầu tâm I(2; 1; -1) tiếp xúc với mặt phẳng (Oyz) nên có bán kính là khoảng cách từ I đến mp(Oyz) và bằng: 2 nên Phương trình mặt cầu là: (x-2)2+(y-1)2+(z-1)2=4.
Vậy chọn A.
Bài 10 (trang 113 sgk Hình Học 12 nâng cao):
Cho ba điểm A(1; 1; 3); B(-1; 3; 2) và C(-1; 2; 3). Mặt phẳng (ABC) có Phương trình là:
A. x+2y+2z-3=0 B. x-2y+3z-3=0
C. x+2y+2z-9=0 D. x2+2y+2z+9=0
Lời giải:
Mặt phẳng (ABC) là mặt phẳng đi qua A(1; 1; 3) và nhận vectơ [AB→,AC→ ] làm vectơ pháp tuyến. ta có [AB→,AC→]=(1;2;1) nên mp(ABC) có Phương trình là: x+2y+2z-9=0.
Vậy chọn C.
Bài 11 (trang 113 sgk Hình Học 12 nâng cao):
Cho ba điểm A(1, 0, 0); B(0; 2; 0) và C(0; 0; 3). Phương trình nào sau đây không phải là Phương trình mặt phẳng (ABC)?
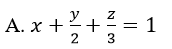
C. 6x+3y+2z+6=0
D. 12x+6y+4z-12=0
Lời giải:
Mặt phẳng (ABC) có phương trình viết đoạn chắn là:
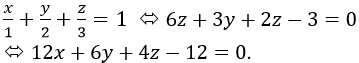
Vậy chọn D.
Bài 12 (trang 113 sgk Hình Học 12 nâng cao):
Cho hai điểm A(1; 3; -4) và B(-1; 2; 1). Phương trình mặt phẳng trung trực của đoạn AB là:
A. 4x+2y-12z-17=0 B. 4x+2y+12z-17=0
C. 4x-2y-12z-17=0 D. 4x-2y+12z-17=0
Lời giải:
Mặt phẳng trung trực của đoạn AB đi qua trung điểm I(0;5/2; -1) của AB và nhận AB→(-2; -1;6) làm vectơ pháp tuyến, nên mặt phẳng có phương trình là:
-2x-(y-5/2)+6(z+1)=0
<=> -4x-2y+12z+17=0 <=> 4x+2y-12z-17=0.
Vậy chọn A.
Bài 13 (trang 114 sgk Hình Học 12 nâng cao):
Cho A(a, 0, 0); B(0; b; 0), C(0; 0; c), a, b, c là những số dương thay đổi sao cho
![]()
Mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là:
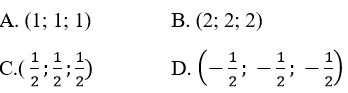
Lời giải:
Phương trình mặt phẳng (ABC) viết theo đoạn chắn là:
![]()
nên ta thấy (ABC) đi qua điểm (1/2;1/2;1/2).
Vậy chọn C.
Bài 14 (trang 114 sgk Hình Học 12 nâng cao):
Cho điểm A(-1; 2; 1) và hai mặt phẳng (P): 2x+4y-6z-5=0 và (Q): x+2y-3z=0. Mệnh đề nào sau đây đúng?
A. mp(Q) đi qua A và song song với (P).
B. mp(Q) không đi qua A và song song với (P)
C. mp(Q) đi qua A và không song song với (P)
D. mp(Q) không đi qua A và không song song với (P)
Lời giải:
Thay tọa độ của điểm A(-1; 2; 1) và Phương trình mp(Q) ta thấy thỏa mãn, nên (Q) đi qua A.
Mặt khác

Nên (P) và (Q) song song với nhau. Vậy chọn A.
Bài 15 (trang 114 sgk Hình Học 12 nâng cao):
Cho điểm A(1; 2; -5). Gọi M, n, P là hình chiếu của A trên ba trục Ox, Oy, Oz. Phương trình mặt phẳng (MNP) là:
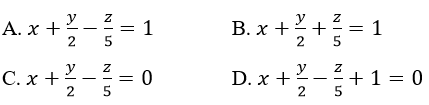
Lời giải:
Vì M, N, P là hình chiếu của A(1; 2; -5) lên ba trục Ox, Oy, Oz nên ta có: M(1; 0; 0); N(0; 2; 0); P(0;0; -5)
Vậy mp(MNP) có phương trình là:
![]()
Vậy chọn A.
Bài 16 (trang 114 sgk Hình Học 12 nâng cao):
Cho mặt cầu (S): x2+y2+z2-2(x+y+z)-22=0 và mặt phẳng (P): 3x-2y+6z+14=0. Khoảnh cách từ tâm I của mặt cầu S tới mặt phẳng P là:
A. 1 B. 2 C. 3 D. 4
Lời giải:
Tọa độ tâm mặt cầu (S) là I = (1; 1; 1). Khoảng cách từ I(1; 1; 1) đến mp(P): 3x-2y+6z+14=0 là:
![]()
Vậy chọn C.
Bài 17 (trang 114 sgk Hình Học 12 nâng cao):
Mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C trọng tâm tam giác ABC là G(-1; -3; 2). Phương trình mặt phẳng (P) là:
A. x+y-z-5=0 B. 2x-3y-z-1=0
C. x+3y-2z+1=0 D. 6x+2y-3z+18=0
Lời giải:
Vì G(-1; -3; 2) là trọng tâm tam giác ABC với A(a; 0; 0); B(0; b; 0), C(0; 0; c) nên ta có:
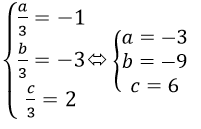
Vậy phương trình mp(ABC) là:
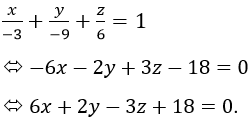
Vậy chọn A.
Bài 18 (trang 115 sgk Hình Học 12 nâng cao):
Cho hình lập Phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M là trung điểm cạnh BC. Tính khoảng cách từ A tới mp (A’MD). Một học sinh giải như sau:
Bước 1. Chọn hệ trục tọa độ như hình bên. Kéo dài DM cắt AB tại E. khi đó, A = (0; 0; 0), E =(2; 0; 0), D = (0; 1; 0); A’ = (0; 0; 1)
Bước 2. Viết Phương trình mặt phẳng (A’MD)
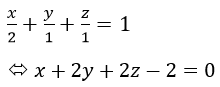
Bước 3. Khoảng cách
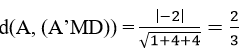
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
A. Đúng
B. Sai ở bước 1
C. Sai ở bước 2
D. Sai ở bước 3
Lời giải:
Học sinh giải đúng. Vậy chọn A.
Bài 19 (trang 115 sgk Hình Học 12 nâng cao):
Cho hai điểm A(1; -1; 5) và B(0; 0; 1), Mặt phẳng (P) chứa A, B và song song với Oy có phương trình là:
A. 4x-z+10 B. 4x+y-z+1=0
C. 2x+z-5=0 D. y+4z-1=0
Lời giải:
Mặt phẳng (P) chứa A, B song song với Oy sẽ có vectơ pháp tuyến là: [AB→,J→]. Trong đó AB→=(-1;1; -4),J→=(0;1;0) là vectơ chỉ Phương của Oy ta tính được [AB→,J→]=(4;0; -1)
Nên mp(P) có Phương trình là: 4x-z+1=0. Vậy chọn A.
Bài 20 (trang 115 sgk Hình Học 12 nâng cao):
Mặt phẳng (P) chứa Oz và điểm A(2, -2, 5) có phương trình là:
A. 2x + 3y = 0 B. 2x – 3y = 0
C. 3x + 2y = 0 D. 3x – 2y + z = 0
Lời giải:
Mặt phẳng (P) chứa Oz và điểm A(2; -3; 5). Vì mặt phẳng (P) chứa trục Oz nên có phương trình dạng Ax + By + Cz + D = 0, vì mp(P) đi qua A(2; -3; 5) nên ta có: 2A – 3B = 0, chọn A = 3 => B = 2 (vì A2+B2 ≠ 0)
Vậy mp(P) có phương trình: 3x+2y=0. Vậy chọn C.
Bài 21 (trang 116 sgk Hình Học 12 nâng cao):
Cho mặt phẳng (P) có chứa Phương trình x – y – 1 = 0. Điểm H(2; -1; -2) là hình chiếu vuông góc của gốc tọa độ O lên một mặt phẳn (Q). Góc giữa hai mặt phẳng (P) và (Q) bằng:
A. 30o B. 45o C. 60o D. 90o
Lời giải:
Vì mp(Q) chứa điểm H là hình chiếu vuông góc của O nên mp(Q) đi qua H và nhận OH→=(2; -1; -2) làm vectơ pháp tuyến, nên mp(Q) có góc giữa (P) và (Q) được xác định theo công thức:
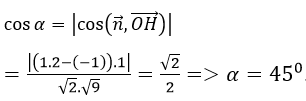
Vậy chọn B.
Bài 21 (trang 116 sgk Hình Học 12 nâng cao):
Cho mặt phẳng (P) có chứa Phương trình x – y – 1 = 0. Điểm H(2; -1; -2) là hình chiếu vuông góc của gốc tọa độ O lên một mặt phẳn (Q). Góc giữa hai mặt phẳng (P) và (Q) bằng:
A. 30o B. 45o C. 60o D. 90o
Lời giải:
Vì mp(Q) chứa điểm H là hình chiếu vuông góc của O nên mp(Q) đi qua H và nhận OH→=(2; -1; -2) làm vectơ pháp tuyến, nên mp(Q) có góc giữa (P) và (Q) được xác định theo công thức:
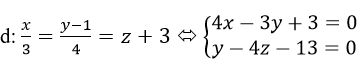
Vậy chọn B.
Bài 23 (trang 116 sgk Hình Học 12 nâng cao):
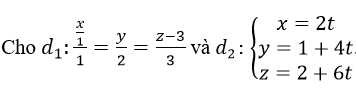
Khẳng định nào sau đây là đúng?
A. d1,d2 cắt nhau B. d1,d2 trung nhau
C. d1//d2 D. d1,d2 chéo nhau
Lời giải:
d1 đi qua M1 (1;0;3) có vectơ chỉ phương là u1→=(1;2;3)
d2 đi qua M2 (0;1;2) có vectơ chỉ phương là u2→=(2;4;6)
Ta thấy u1→ và u1→ cùng Phương, chứng tỏ d1 và d2 song song hoặc trùng nhau. Mặt khác điểm M1 (1;0;3) không thuộc (2). Vậy d1 // d2.
Vậy chọn C.
Bài 24 (trang 116 sgk Hình Học 12 nâng cao):
Cho mặt phẳng (α):x+3y+x+1=0 và đường thẳng
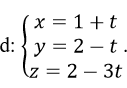
Tọa độ giao điểm A của d và (α) là:
A. A(3; 0; 4) B. A(3; -4; 0)
C. A(-3; 0; 4) D. A(3; 0; -4)
Lời giải:
Thay x, y, z ở Phương trình của d vào Phương trình của (α) ta được:
1+t+3(2-t)+2-3t+1=0 <=> -5t+10=0 <=> t = 2
Thay t = 2 vào phương trình d ta được
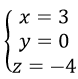
Vậy chọn D.
Bài 25 (trang 116 sgk Hình Học 12 nâng cao): Cho đường thẳng
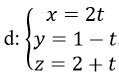
Phương trình nào sau đây cũng là phương trình của đường thẳng d?
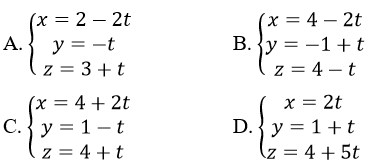
Lời giải:
Đường thẳng d đi qua M(0; 1; 2) và vectơ chỉ phương u→=(2; -1;1) nên d có phương tham số là
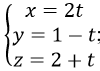
đường thẳng d còn đi qua điểm M’(4; -1; 4) ứng với t = 2 và có vectơ chỉ phương u’→=(-2;1; -1) nên Phương trình tham số của d còn viết dưới dạng:
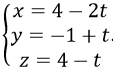
Vậy chọn B
Bài 26 (trang 117 sgk Hình Học 12 nâng cao):
Cho hai điểm A(2, 3, -1) và B(1, 2, 4) và ba phương trình sau:
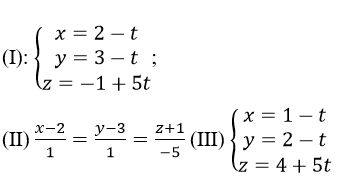
Mệnh đề nào sau đây đúng ?
A. Chỉ (I) là Phương trình của đường thẳng AB.
B. Chỉ (III) là Phương trình của đường thẳng AB.
C. Chỉ (I) và (II) là phương trình của đường thẳng AB.
D. Cả (I), (II) và (III) đều phương trình của đường thẳng AB.
Lời giải:
Đường thẳng AB đi qua A(2; 3; -1) và B(1; 2; 4) có vectơ chỉ phương là (AB) ⃗=(-1; -1;5) nên đường thẳng AB có phương trình là:
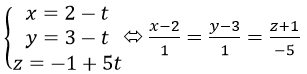
hoặc AB còn có phương trình là:
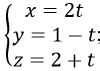
Vậy chọn D.
Bài 27 (trang 117 sgk Hình Học 12 nâng cao):
Cho ba điểm A(1, 3, 2); B(1, 2, 1), C(1, 1, 3). Viết phương trình đường thẳng Δ đi qua trọng tâm G của tam giác ABC và vuông góc với mp(ABC). Một học sinh giải như sau:
Bước 1. Tọa độ trọng tâm của ABC là
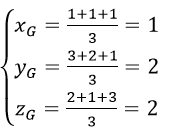
Bước 2. Vectơ pháp tuyến của mp(ABC) là: n→=[AB→,AC→]=(-3;1;0)
Bước 3. Phương trình tham số của đường thẳng Δ là:
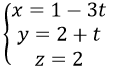
Bài giải trên đúng hay sai, nếu sai thì sai ở bước nào?
A. Đúng B. Sai ở bước 1
C. Sai ở bước 2 D. Sai ở bước 3
Lời giải:
Chọn C
Bài 28 (trang 118 sgk Hình Học 12 nâng cao):
Gọi d là đường thẳng qua gốc tọa đô O, vuông góc với trục Ox và vuông góc với thẳng A:
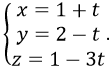
Phương trình của d là:
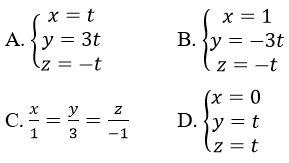
Lời giải:
Chọn D
Bài 29 (trang 118 sgk Hình Học 12 nâng cao): Cho đường thẳng
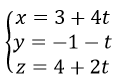
và mặt phẳng (P): x+2y-z+3=0. Trong các mệnh đề sau, mệnh đề nào đúng?
A. d song song với (P) B. d cắt (P)
C. d vuông góc với (P) D. d nằm trên (P)
Lời giải:
Chọn D
Bài 30 (trang 118 sgk Hình Học 12 nâng cao):
Cho điểm A(1, 1, 1) và đường thẳng
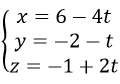
Hình chiếu của A trên d có tọa độ là:
A. (2; -3; 1) B. (2; -3; -1)
C. (2; 3; 1) D. (-2; 3;1)
Lời giải:
Hình chiếu vuông góc của A lên d là giao điểm của mp(α) đi qua A vuông góc với d với đường thẳng a.
Mp(α) có phương trình : -x-y+2z+3=0
Từ đó tìm được giao điểm H của d và (α) là: H = (2; -3; 1).
Vậy chọn A.
Bài 31 (trang 119 sgk Hình Học 12 nâng cao):
Cho tứ diện ABCD có A(1; 0; 0), B(1; 1;0); C(0; 1; 0) và D(0; 0; 2). Tính khoảng cách giữa AC và BD.
Một học sinh giải như sau:
Bước 1. AC→=(-1;1;0),BD→=(-1; -1;2),AB→=(0;1;0)
Bước 2. [AC, BD]=(2;2;2)
Bước 3.
![]()
Bài giải trên đúng hay sai, nếu sai thì sai ở bước nào?
A. Đúng B. Sai ở bước 1.
C. Sai ở bước 2 D. Sai ở bước 3
Lời giải:
Khoảng cách giữa AC và BD được xác định theo công thức:
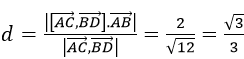
Vậy học sinh đúng. Vậy chọn A.
Bài 32 (trang 119 sgk Hình Học 12 nâng cao):
u→ |=2;|v→ |=1,(u→+v→ )=π/3. Góc giữa v→ và u→–v→ bằng:
A. 30o B. 45o C. 60o D. 90o
Lời giải:
Ta có: u→,v→=|u→||v→ | cos(u→,v→)=2.cos(π/3)=2.(1/2)=1
(u→+v→ )2=u→2+2u→.v→+v→2=4+2+1=7
(u→–v→ )2=u→.v→–v→2=1-1=0
Vậy u→–v→⊥v→. Vậy chọn D.
Bài 33 (trang 119 sgk Hình Học 12 nâng cao):
|u→|=2;|v→ |=5,(u→,v→ )=π/6. Độ dài vectơ [u ⃗,v ⃗] bằng:
A. 10 B. 5 C. 8 D. 5 √3
Lời giải:
[u→,v→]=|u→ ||v→ | sin(u→,v→)=2.5.sin(π/6)=5.
Chọn B.
Bài 34 (trang 119 sgk Hình Học 12 nâng cao):
Mặt phẳng 2x-3y+z-1=0 cắt trục tọa độ tại các điểm:
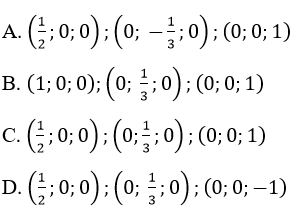
Lời giải:
Mặt phẳng 2x-3y+z-1=0 cắt trục Ox, Oy, Oz lần lượt tại:
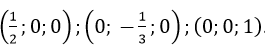
Vậy chọn A.
Bài 35 (trang 120 sgk Hình Học 12 nâng cao):
Cho đường thẳng: d:
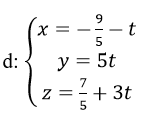
và mặt phẳng (P): 3x-2y+3z-1=0. Gọi d’ là hình chiếu của d trên (P). trong các vectơ sau, vectơ nào không phải là vectơ chỉ Phương của hình chiếu d trên (P).
A. (5; -51; -39) B. (10; -102; -78)
C. (-5; 51; 39) D. (5; 51; 39)
Lời giải:
Trong 4 phương án đã cho u1→(5; -55; -39);u2→(10; -102; -78);u3→(-5;51;39);u4→(5;51;39)
Ta thấy u1→,u2→,u1→ là vectơ cùng phương và không cùng phương với u4→.
Vậy u4→ không phải vectơ chỉ phương của d’.
Vậy chọn D.
Bài 36 (trang 120 sgk Hình Học 12 nâng cao):
Cho hình lập Phương ABCD.A’B’C’D’ cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của A’B’, BC, DD’. Chứng minh rằng AC’ ⊥ (MNP). Một học sinh giải như sau:
Bước 1. Chọn hệ trục tọa độ như hình bên.
Khi đó A = (0; 0; 0), C’ (1; 1; 1)
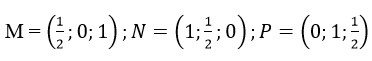
Bước 2. Tính (AC’) ⃗=(1;1;1)
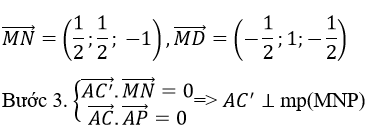
Bài giải trên đúng hau sai, nếu sai thì sai ở bước nào?
A. Đúng B. Sai ở bước 1.
C. Sai ở bước 2 D. Sai ở bước 3
Lời giải:
Học sinh giải đúng. Chọn A.
Bài 37 (trang 121 sgk Hình Học 12 nâng cao): Cho đường thẳng d:
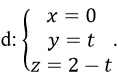
Phương trình đường vuông góc chung của d và trục Ox là:
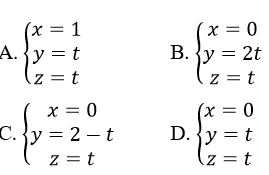
Lời giải:
Chọn D.
Bài 38 (trang 121 sgk Hình Học 12 nâng cao):
Cho mặt phẳng (P): x-2y-3z+14=0 và điểm M(1; -1; 1). Tọa độ điểm M’ đối xứng với M qua mp(P) là:
A. (-1; 3; 7) B. (1; -3; 7) C. (2; -3; -2) D. (2; -1; 1)
Lời giải:
Đường thẳng MM’ là đường thẳng đi qua M(1; -1; 1) và nhận vectơ pháp tuyến của (P) là n ⃗=(1;-2;-3) làm vectơ chỉ phương nên MM’ có phương trình
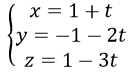
Tọa độ điểm H của MM’ và mp(P) là nghiệm của hệ
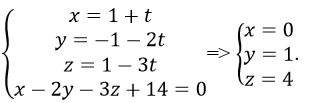
Vậy H(0; 1; 4)
Vì M và M’ đối xứng qua mp(P) nên H là trung điểm của MM’ suy ra:
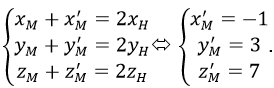
vậy M(-1; 3; 7). Vậy chọn A.
Bài 39 (trang 121 sgk Hình Học 12 nâng cao):
Cho điểm A(0; -1; 3) và đường thẳng d:
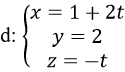
Khoảng cách từ A đến d bằng:
A. √3 B. √14 C. √6 D. √8
Lời giải:
Đường thẳng (d) đi qua M(1; 2; 0) và có vectơ chỉ phương u→=(2;0; -1) khoảng cách từ A(0; -1; 3) đến d được xác định như sau:
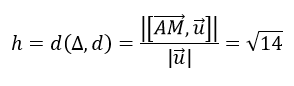
Vậy chọn B
Bài 40 (trang 121 sgk Hình Học 12 nâng cao):
Cho điểm M(-1; 2; -3). Gọi M1,M2,M3 lần lượt là điểm đối xứng của M qua mặt phẳng (Oxy), (Oxz), (Oyz). Phương trình mp(M1,M2,M3) là:
A. 6x+2y+3z+6=0 B. 6x-2y+3z+6=0
C. 6x-2y+3z+6=0 D. 6x-2y-3z+6=0
Lời giải:
Tọa độ M1,M2,M3 lần lượt là: M1 (-1;2;3),M2 (-1; -2; -3),M3 (1;2; -3). Khi đó ta tìm được mp(P) (M1 M2 M3) là:
6x-3y+2z+6=0.
Vậy chọn C.
Bài 41 (trang 122 sgk Hình Học 12 nâng cao):
Cho mặt cầu (S): (x-1)2+(y-3)2+(z-2)2=49. Phương trình nào sau đây là Phương trình tiếp xúc với mặt cầu (S)?
A. 6x+2y+3z=0 B. 6x+2y+3z-5=0
C. 6x+2y+3z-55=0 D. 6x-2y+3z-7=0
Lời giải:
Mặt cầu (S): (x-1)2+(y+3)2+(z-2)2=49 có tâm là:
I=(1;-3;2), có bán kính là R=7.
Khoảng cách từ tâm I(1; -3; 2) đến mặt phẳng: 6x+2y+3z-55=0. Là:
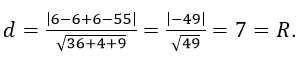
Vậy mặt cầu (S) tiếp xúc với mặt phẳng: 6x+2y+3z-55=0.
Vậy chọn C.
Bài 42 (trang 122 sgk Hình Học 12 nâng cao):
Cho mặt cầu (S): x2+y2+z2-2x-4y-6z=0. Trong ba điểm (0; 0; 0), (1; 2; 3); (2; -1; -1) có bao nhiêu nằm trong mặt cầu (S)?
A. 0 B. 1 C. 2 D. 3
Lời giải:
Chọn C