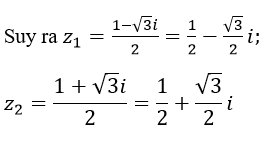
Bài 23 (trang 199 sgk Giải Tích 12 nâng cao):
Giải Phương trình z=(1/z)+k trong các trường hợp sau:
a) k =1 b) k=√2 c) k = 2i
Lời giải:
a) Khi k = 1 ta có Phương trình: z+(1/z)=1, điều kiện z ≠ 0 phương trình:
<=> z2-z+1=0,có Δ=1-4=-3=(√3 i)2
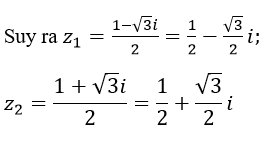
b) Khi k = √2 ta có Phương trình: z2-√2 z+1=0
có Δ=2-4=-2=(√2 i)2
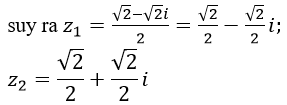
c) Khi k = 2i ta có Phương trình: z2-2iz+1=0
Có Δ=(2i)2-4=-8=(2 √2i)2
Nên suy ra z1=(2i-2 √2 i)/2=(1-√2)i;z2=(1+√2)i
Vậy Phương trình có hai nghiệm là: (1-√2 i) và (1+√2i)
Bài 24 (trang 199 sgk Giải Tích 12 nâng cao):
Giải các phương trình sau và biểu diễn hình học tập hợp các nghiệm của mỗi Phuong trình trong mặt phẳng số phức.
a) z3+1=0
b) z4-1=0
c) z4+4=0
d) 8z4+8z3=z+1
Lời giải:
a) <=> (z+1)(z2-z+1)=0
b) <=> (z-1)(z+1)(z2+1)=0 <=> z=±1 và z=±i
c) <=> ((z2 )2-(2i)2 )2=0 <=> (z2-2i)(z2+2i)=0
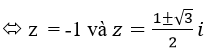
d) <=> 8z3 (z+1)=z+1 <=> (z+1)(8z4-1)=0
<=> (z+1)(2z-1)(4z2+2z+1)=0
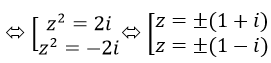
Vậy Phương trình có 4 nghiệm là:
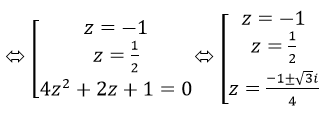
Vậy Phương trình có 4 nghiệm là:
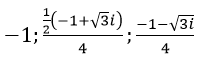
Bài 25 (trang 199 sgk Giải Tích 12 nâng cao):
a) Tìm các số thực a, b để Phương trình (với ẩn z).
z2+bz+c=0 nhận z=1+i làm một nghiệm.
b) Tìm các số thực a, b, c để Phương trình (với ẩn z): z3+az2+bz+c=0 nhận z = 1 +I làm nghiệm và cũng nhận z = 2 làm nghiệm.
Lời giải:
a) Vì z=1+i làm nghiệm đúng của: z2+bz+c=0 nên: (1+i)2+b(1+i)+c=0
<=> 1+2i-1+b+bi+c=0 <=> (b+c)+(2+b)i=0
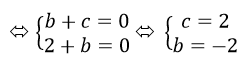
Vậy b = -2 và c = 2 là giá trị cần tìm.
b) Vì z=1+i và z=2 là nghiệm của Phương trình: z3+az2+bz+c=0 nên ta có:
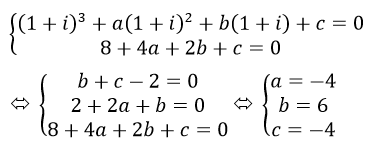
Vậy a = -4 và b = 6 và c = -4 là giá trị cần tìm.
Bài 26 (trang 199 sgk Giải Tích 12 nâng cao):
a) Dùng công thức lượng giác để chứng minh rằng với mọi số thức φ, ta có:
(cosφ+i sinφ )2=cos2φ+isin 2φ
Từ đó hãy tìm mọi căn bậc hai của số thức: cos2φ+isin 2φ. Hãy so sánh cách giải thích này với cách giải thích học ở bài §2.
Lời giải:
a) Ta có: (cosφ+i sinφ )2=(cos2φ-sin2φ )+2sinφcosφi=cos2φ+isin 2φ
Suy ra cos2φ+isin 2φ có căn bậc hai là:
cosφ+i sinφ và -cosφ-i sinφ
nhận xét: các giải thích này rất thuận lợi cho việc tìm căn bậc hai của số phức: z=a+bi với a2+b2=1
Ta có:
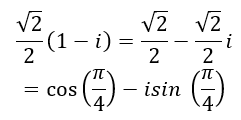
Theo câu a) thì số cos(π/4)-i sin(π/4) có căn bậc hai là:
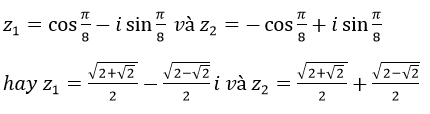
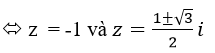
3unconcern
free dating gay black men https://gaypridee.com/
chat gay usa https://gaytgpost.com/
gay random chat https://gay-buddies.com/
black gay dating https://speedgaydate.com/
online slots real money https://candylandslotmachine.com/
in the money slots https://pennyslotmachines.org/
son and moon slots https://slotmachinesforum.net/
play sizzling 7 slots free https://slot-machine-sale.com/
free slots no downloads https://beat-slot-machines.com/
hollywood slots bangor https://411slotmachine.com/
dissertation help statistics https://dissertationwriting-service.com/
Comments are closed.