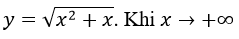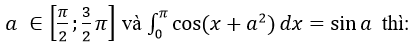Bài 25 (trang 215 sgk Giải Tích 12 nâng cao):
Hàm số y=sin2x-2sinx có giá trị nhỏ nhất là:
A. -1/2 B. 0 C. -1 D. -1/3
Lời giải:
Ta có: f(x) = sin2x-2sinx=(sinx-1)2-1≥1,∀x dấu “=” xảy ra khi sinx = 1 <=> x=π/2+k2 π;k ∈Z
Vậy f(x) có giá trị nhỏ nhất là -1 nên ta chọn C.
Bài 26 (trang 215 sgk Giải Tích 12 nâng cao): Gọi (C) là thị hàm số
![]()
A. Đường thẳng y=x+1 là tiệm cận xiên của (C) khi x->+∞
B. Đường thẳng y=x+1/2 là tiệm cận xiên của C khi x->+∞
C. Đường thẳng y=-x là tiệm cận của C khi x->+∞
D. Đồ thị C không có tiệm cận xiên x->+∞
Lời giải:
Gọi y = ax + b là tiệm cận xiên của đồ thị hàm số
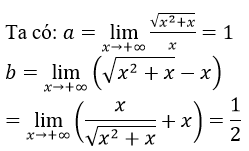
Vậy tiệm cận xiên là y=x+1/2, nên ta chọn B.
Bài 27 (trang 215 sgk Giải Tích 12 nâng cao):
Đồ thị hàm số y=x3-x+1 tiếp xúc tại điểm (1; 1) với.
A Parabol y=2x2-1 B. parabol y=x2
C. parabol y=-x2+2x D. đường thẳng y=2x+1
Lời giải:
Phương trình tiếp tuyến của đô thị hàm số y=x3-x+1 tại điểm (1; 1) là y=2x-1, đây cũng là Phương trình tiếp tuyến của parabol y=x2 tại điểm (1; 1). Vậy đồ thị hàm số tiếp xúc với (P): y=x2 tại (1;1) nên ta chọn B.
Bài 28 (trang 215 sgk Giải Tích 12 nâng cao): Cho hai số dương a và b.
![]()
A. X > Y B. X <l Y C. X ≥ Y D. X ≤ Y
Lời giải:


Với mọi số dương a, b ta có: (a+b)2≥4ab, dấu “=” xảy ra khi a = b.
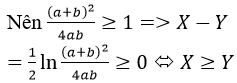
Vậy ta chọn C.
Bài 29 (trang 215 sgk Giải Tích 12 nâng cao):
Cho hai số dương không âm a và b.
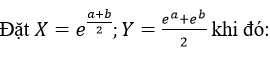
A. X > Y B. X < Y C. X ≥ Y D. X ≤ Y
Lời giải:
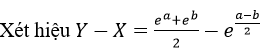
Với mọi số a, b, không âm ta có
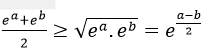
Dấu “=” xảy ra khi a = b.
Vậy Y – X ≥0 <=>Y≥x. nên ta chọn D.
Bài 30 (trang 215 sgk Giải Tích 12 nâng cao):
Cho C là đồ thị hàm số y=log2x, ta có thể suy ra đồ thị của hàm số log2(x+3) bằng cách tịnh tiến C theo vectơ.
A. v→=(3;1) B. v→=(3;-1)
C. v→=(-3;1) D. v→=(-3;-1)
Lời giải:
Gọi v→ =(a;b) là vectơ tịnh tiến cần tìm. Lấy 1 điểm A(x;log2x ) bất kì thuộc C. khi đó ảnh của A qua T là A’(x+a;log2x+b)
Để A’ thuộc đồ thị hàm số y=log22(x+3) thì:
log2x+b=log2(xa+3) đúng với ∀x>0
<=>log2x+b=1+log2(x+a+3) đúng với ∀x>0
Suy ra b = 1 và a = -3. Vậy v→ =(-3;1) là vectơ cần tìm. Vậy chọn C
Bài 31 (trang 216 sgk Giải Tích 12 nâng cao):
Cho hàm số f(x) = log5(x2+1). Khi đó
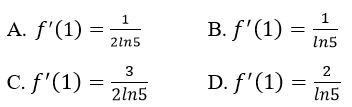
Lời giải:
Ta có
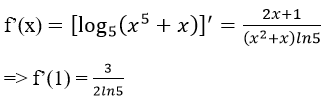
Vậy chọn C.
Bài 32 (trang 216 sgk Giải Tích 12 nâng cao):
Biết đồ thị hàm số y=ax và đồ thị của hàm số y=logbx cắt nhau tại điểm (√(2-1 );2). Ta kết luận:
A. (a>1 và b>1) B. a> 1 và 0 < b < 1
C. 0 < a < 1 và b > 1 D. 0 < a < 1 và 0 < b < 1
Lời giải:
Vì đồ thị hàm số y=ax cắt đồ thị hàm số y=logbx tại (√(2-1 );√2) nên điểm (1/√2;√2 ) thuộc cả hai đồ thị đó.
Ta có:
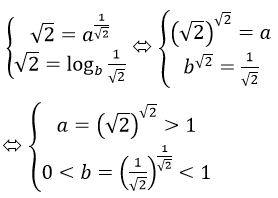
Vậy chọn B.
Bài 33 (trang 216 sgk Giải Tích 12 nâng cao):
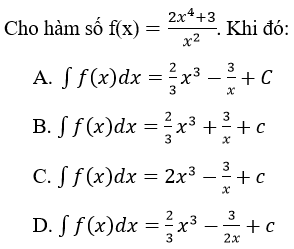
Lời giải:

Vậy chọn A
Bài 34 (trang 216 sgk Giải Tích 12 nâng cao):
Nếu a là một số thỏa mãn các điều kiện:
![]()
A. a=π B. a=√π C. a=2√π D. a=√(2 π)
Lời giải:
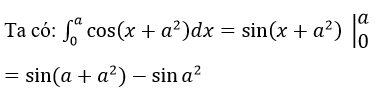
Theo bài ra ta có: sin(a+a2)-sina2=sina
<=> sin(a+a2)=sina2 +sina

Vậy chọn D.
Bài 34 (trang 216 sgk Giải Tích 12 nâng cao): Nếu a là một số thỏa mãn các điều kiện:
A. a=π B. a=√π C. a=2√π D. a=√(2 π)
Lời giải:
![]()
Theo bài ra ta có: sin(a+a2)-sina2=sina
<=> sin(a+a2)=sina2 +sina

Vậy chọn D.
Bài 36 (trang 217 sgk Giải Tích 12 nâng cao):
Cho số phức z tùy ý. Xét các số phức
![]()
Khi đó:
A. α là số thực, β là số thực. B. α là số thực, β là số ảo.
C. α là số ảo, β là số thực. D. α là số ảo, β là số ảo.
Lời giải:
Giả sử z=a+bi, ta có:
α=(a+bi)2+(a-bi)2=2a2 vậy α ∈R
β=(a+bi)(a-bi)+i(a+bi-a+bi)=a2+b2-b2)= a2 ∈R
Vậy chọn A.
Bài 37 (trang 217 sgk Giải Tích 12 nâng cao): Cho số phức tùy ý z ≠ 1. Xét các số phức.
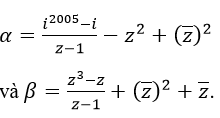
Khi đó:
A. α là số thực, β là số thực. B. α là số thực, β là số ảo.
C. α là số ảo, β là số thực. D. α là số ảo, β là số ảo.
Lời giải:
Giả sử z=a+bi (z ≠ 1), ta có:
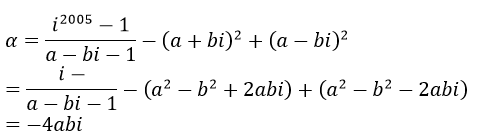
Vậy α là một số ảo
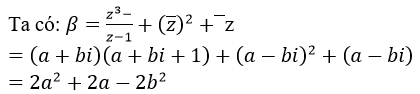
Vậy β là một số thực. vậy chọn C.
Bài 38 (trang 217 sgk Giải Tích 12 nâng cao):
Nếu mô đun của số phức z bằng r (r > 0) thì mô đun của số phức (1-i)2 z. Bằng.
A. 4r B. 2r C. r √2 D. √2
Lời giải:
![]()
Ta có (1-i)2 x=(1-2i-1)(a+bi)=2b-2ai) có mô đun là:
![]()
Vậy chọn B.