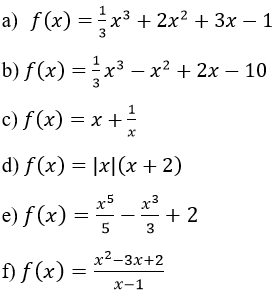
Bài 11 (trang 16 sgk Giải Tích 12 nâng cao):
Tìm cực trị của các hàm số sau:
Lời giải:
a) Hàm số đã cho xác định trên R.
Ta có: f’(x) = x2+4x+3
Từ đó f’(x) = 0 <=> x = -1 hoặc x = -3
Bảng biến thiên
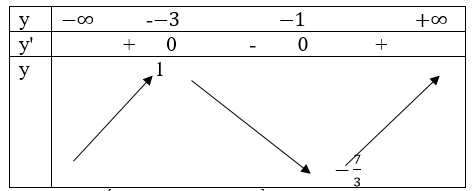
Vậy hàm số đạt cực đại tại điểm x = -3, giá trị cực đại của hàm số là: fCĐ=f(-3)=-1.
Hàm số đạt cực tiểu tại điểm x = -1, giá trị cực tiển của hàm số là fCT=f(-1)=-7/3
b) Tập xác định: R
f’ (x)=x2-2x+2=(x-1)2+1>0,∀x ∈R=>f(x) luôn đồng biến nên hàm số không có cực trị.
c) Tập xác định: R \ {0}
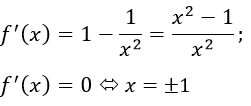
Bảng biến thiên
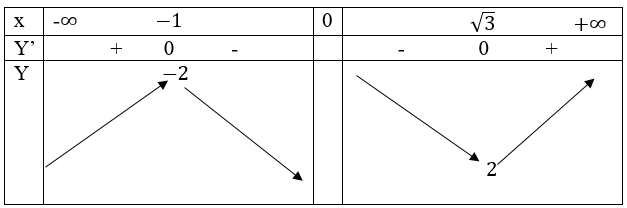
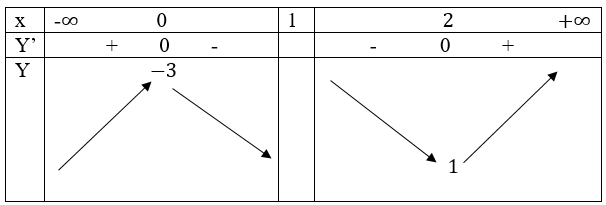
Vậy hàm số cực đại tại x = -1; fCĐ=f(-1)=-2
Hàm số cực tiểu tại x = 1; fCT=f(1)=2
d) f(x) xác định liên tục trên R.
ta có:
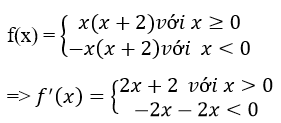
bảng biến thiên:
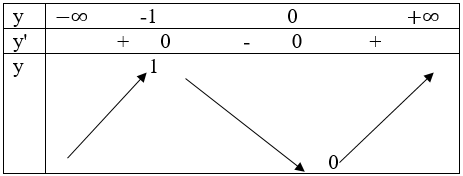
Hàm số đạt cực đại tại x = -1, fCĐ=f(-1)=1
Hàm số đạt cực tiểu tại x = 0, fCT=f(0)=1
e) tập xác định: R
f’(x) = x4-x2;f’ (x)=0 <=> x = 0 hoặc x=±1
bảng biến thiên:
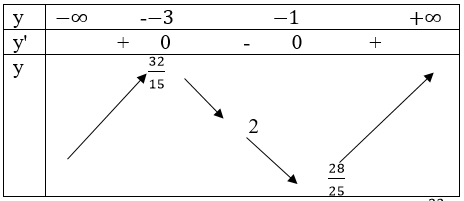
Vậy hàm số đạt cực đại tại x = -1, fCĐ=f(-1)=32/15
Hàm số cực tiểu tại x = 1; fCT=f(1)=28/15
f) Tập xác định: R \ {1}
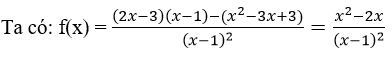
f’ (x)=0 <=> x = 0 hoặc x = 2
Bảng biến thiên:
Bài 12 (trang 17 sgk Giải Tích 12 nâng cao):
Tìm cực trị của hàm số sau:
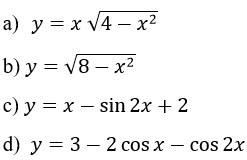
Lời giải:
a) Tập xác định: [-2; 2]
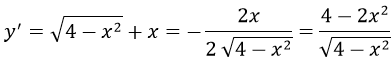
y’=0 <=> x=±√2
Bảng biến thiên:
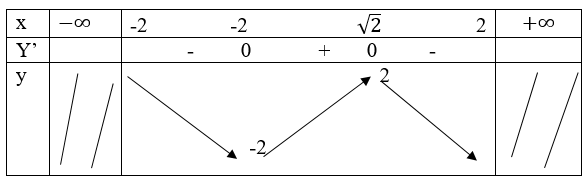
Hàm số đạt cực tiểu tại x=-√2,yCT=y(-√2 )=-2
Hàm số đạt cực đại tại x = √2,yCĐ=y(√2)=2
b) Tập xác định: [-2√2;2√2]
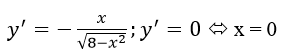
Bảng biến thiên:
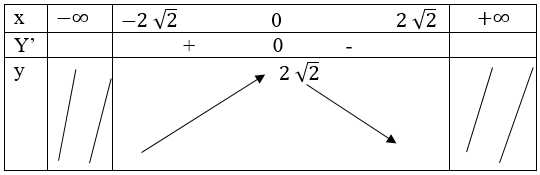
Hàm số cực đại tại x = 0; yCĐ=y(0)=2√2
Hàm số không có cực tiểu.
c) Tập xác định: R
y’=(x-sin2x+2)’=1-2 cos2x
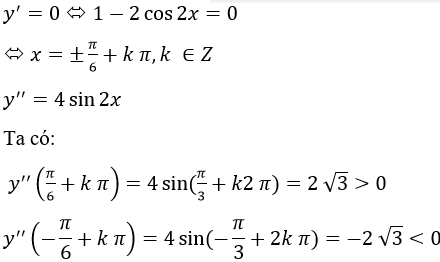
Vậy hàm số cực đại tại điểm

Hàm số đạt cực tiểu tại tiểu
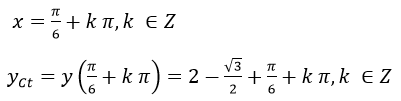
d) Tập xác định: R
y’=2 sinx+2.sin2x=2 sinx(1+2 cosx )
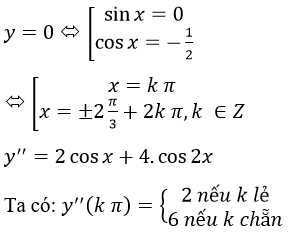
=> y” (k π)>0 (có thể viết: y” (k π)=4+2 cos(k π)
Nên hàm số đạt cực tiểu tại các điểm
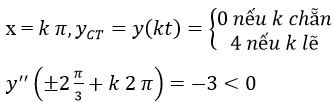
nên hàm số đạt cực đại tại các điểm.
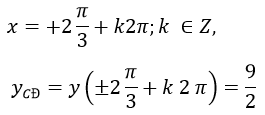
Bài 13 (trang 17 sgk Giải Tích 12 nâng cao):
Tìm các hệ số a, b, c, d của hàm số f(x) = ax^3+bx^2+cx+d sao cho hàm số đạt cực tiểu tại điểm x = 0; f(0) = 0 đạt cực đại tại điểm x = 1, f(1) = 1
Lời giải:
Ta có f’(x) = 3ax2+2bx+c=>f’ (0)=c;f’ (1)=3a+2b+c
Vì f(0) = 0 =>d= 0
Hàm số đạt cực tiểu tại x = 0 nên f’(0) = 0 => c =0; f(1) = a + b = 1
Hàm số đạt cực đại tại điểm x = 1 nên f’(1) = 0 => 3a + 2b = 0
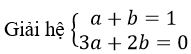
ta được a = -2; b = 3
Vật f(x) = -2x2+3x2
Thử lại f’(x) = -6x2+6x;f” (x)=-12x+6
f’’(0) > 0. Hàm số đạt cực tiểu tại điểm x = 0
f’’(1) = -6 < 0. Hàm số đạt cực đại tại x = 1
Đáp số: a = -2; b = 3; c =3; d = 0
Bài 14 (trang 17 sgk Giải Tích 12 nâng cao):
Xác định các hệ số a, b, c sao cho hàm số: (x) = x3+ax2+bc+c đạt cực trị bằng 0 tại x = -2 và đồ thị của hàm số đi qua A(1; 0)
Lời giải:
f'(x) = 3x2+2ax+b
Điền kiện cần:
Hàm số đạt cực trị bằng 0 tại x = -2 => f’(2) = 0 và f(-2) = 0
Hay -4a+b+12=0 (1)và 4a-2b+c-8=0 (2)
Đồ thị đi qua A(1; 0) => a+b+c+1=0
Giải hệ Phương trình (1), (2), (3) ta được a =3; b = 0; c = -2
Điều kiện đủ:
Xét f(x) = x3+3x2-4. Ta có: đồ thị hàm số f(x) đi qua A(1; 0)
f’(x) = 3x3+6x=>f” (x)=6x+6
f’(-2)= 0; f’’(2) = -6 < 0 nên x = -2 là điểm cực đại và f(-2) = 0
Đáp số:a =3; b =0; c = -4
Bài 15 (trang 17 sgk Giải Tích 12 nâng cao):
Chứng minh rằng với mọi giá trị của m, n hàm số luôn có cực đại và cực tiểu..
Lời giải:
Hàm số được viết lại là:
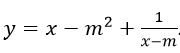
Hàm số xác định ∀x ≠ m
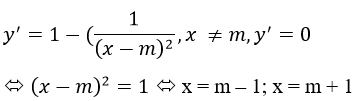
Bảng biến thiên
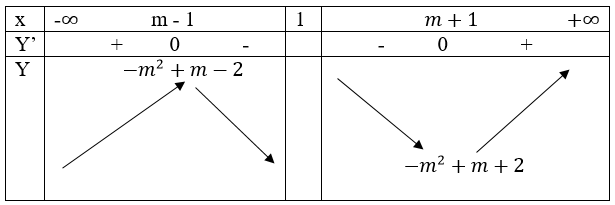
Vậy với mọi giá trị của m, hàm số đạt được cực đại tại x = m -1 và đạt cực tiểu tại x = m + 1
2bacteria
fre gay chat https://bjsgaychatroom.info/
gay dating advice https://gaypridee.com/
chat ave gay https://gay-buddies.com/
gay teen dating sites https://speedgaydate.com/
nude slots for free https://freeonlneslotmachine.com/
myvegas slots https://candylandslotmachine.com/
baba wild slots casino https://pennyslotmachines.org/
ff tactics 24 slots https://slotmachinesworld.com/
vegas slots online https://slotmachinesforum.net/
argosy free fun slots https://beat-slot-machines.com/
liberty slots https://download-slot-machines.com/
300 free slots of vegas https://411slotmachine.com/
vegas wotld slots https://slotmachinegameinfo.com/
are dissertation writing services legal https://buydissertationhelp.com/
dissertation writing help uk https://helpon-doctoral-dissertations.net/
Comments are closed.