
Bài 1 (trang 124 sgk Hình Học 12 nâng cao):
Cho H là hình chóp tứ giác đều S.ABCD. xét các mặt phẳng (SAC), (SAB), (ABC), (SOI), trong đó I là trung điểm của AB, O làm tâm của hình vuông ABCD. Trong các mặt phẳng đó, có bao nhiêu mặt phẳng đối xứng của H?
A. 1 B. 2 C. 3 D. 4
Lời giải:
Dựa vào tính chất tứ giác đều thì H có ba mặt phẳng đối xứng là , (SAC), (SBD), (SOI).
Chọn C.
Bài 2 (trang 124 sgk Hình Học 12 nâng cao):
Gọi H lăng trụ đều ABCDEF.A’B’C’D’E’F’. Xét các mặt phẳng: mp(AA’D), mp(ACA’) mặt phẳng trung trực của DD’, mp(ABB’), mặt phẳng trung trực của AB. Trong các mặt phẳng đó có bao nhiêu mặt phẳng đối xứng của H?
A. 1 B. 2 C. 3 D.4
Lời giải:

Dựa vào tính chất của lăng trụ lục giác đều thì các mặt phẳng: (AA’D); mặt phẳng trung trục của DD’; mặt phẳng trung trực của AB là mặt phẳng đối xứng của H.
Chọn C.
Bài 3 (trang 125 sgk Hình Học 12 nâng cao):
Cho khối lăng trụ tam giác ABC.A’B’C’, M là trung điểm cạnh AB. Trong các đẳng thức sau đây, đẳng thức nào sai.
A. VA’B’C’D’=VMA’B’C’
B. VABCC’=VABCC’
C. VMA’B’C’=VA’ABC
D. VMA’B’C’=VAA’B’C’/2
Lời giải:
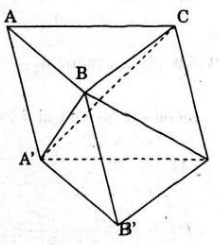
Gọi h là độ dài đường cao của lăng trụ, và S là diện tích tam giác ABC. Ta có:
d(C,(A’B’C’))=d(M,(A’B’C))=h
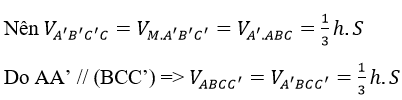
Vậy (A) và (B) và (C) là các đẳng thức đúng.
Chọn D.
Bài 4 (trang 125 sgk Hình Học 12 nâng cao):
Cho khối lăng trụ tam giác ABC.A’B’C’. Trong các đẳng thức sau đây, đẳng thức nào sai?
Lời giải:
Gọi h là độ dài đường cao của lăng trụ S là diện tích ΔABC.
Ta có: VABC.A’B’C’=h.S
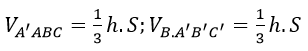
Suy ra
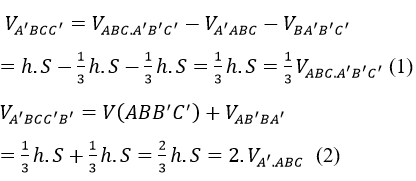
Do CC’ // mp(ABB’A’) =. VC.ABB’A’=VC’ABB’A’ (3)
Từ (1), (2) và (3) suy ra: (a), (B), (C), (D) đẳng thức đúng, B sai.
Chọn B
Bài 5 (trang 125 sgk Hình Học 12 nâng cao):
Cho khối chóp tứ giác S.ABCD và các điểm A’, B’, C’, D’ lần lượt nằm trên các đường thẳng SA, SB, SC, SD nhung không trùng với S. Trong các mệnh đề sau đây, mệnh đề nào đúng?
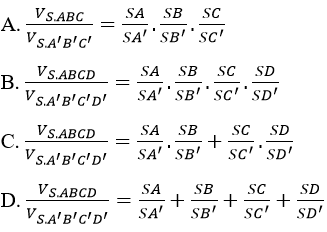
Lời giải:
Mệnh đề (A)
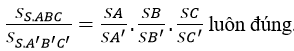
Chọn A
Bài 6 (trang 125 sgk Hình Học 12 nâng cao):
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình lăng trụ nội tiếp được một mặt cầu nếu đáy là đa giác nội tiếp.
B. Hình lăng trụ nội tiếp được một mặt cầu nến có tất cả mặt đều là đa giác nội tiếp.
C. Hình lăng trụ nội tiếp được một mặt cầu nếu có mặt bên vuông góc với mặt đáy.
D. Đa diện nội tiếp được một mặt cầu nếu các mặt đều là đa giác nội tiếp.
Lời giải:
Chỉ có mệnh đề (B) hình lăng trụ nội tiếp mặt cầu nếu tất cả các mặt cầu đều là đa giác nội tiếp là mệnh đề đúng. Các mệnh đề còn lại không đúng (chúng ta chứng minh bằng cách đưa ra 1 phản ví dụ).
Chọn B
Bài 7 (trang 125 sgk Hình Học 12 nâng cao):
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đường tròn đi qua ba điểm phân biệt nằm trên mặt cầu thi nằm hoàn toàn trên mặt cầu.
B. Có duy nhất một mặt cầu đi qua 4 đỉnh của một hình thang cân cho trước.
C. Hình chóp có đáy là hình thang vuông luôn luôn nội tiếp một mặt cầu.
D. Cả ba mệnh đề trên đều đúng.
Lời giải:
Chỉ có mệnh đề A Đường tròn đi qua 3 điểm phân biệt nằm trên mặt cầu thì nằm hoàn toàn trên mặt cầu là mệnh đề đúng.
Chọn A
Bài 8 (trang 126 sgk Hình Học 12 nâng cao):
Cho khối trụ có bán kính a√3 và chiều cao 2a√3 . Trong các số sau đây, số nào là thể tích của nó?
A. 4 πa2√2 B. 9a3√3 C. 6 πa3√3 D. 6 πa2√3
Lời giải:
Thể tích khối trụ là: V=h πR2=2a√3 π(a√3 )2=6 πa3√3
Bài 9 (trang 126 sgk Hình Học 12 nâng cao):
Đáy hình chóp là hình vuông diện tích bằng 4. Các mặt bên là nhũng ta giác đều, diện tích toàn phần của hình chóp là:
A. 4+4√3 B. 8 C. 16 D. 4+4√2
Lời giải:
Diện tích toàn phần của hình chóp tứ giác đều đã cho là: S = 4, diện tích mặt bên + diện tích đáy.
Tròn đó diện tích đáy bằng 4 => đáy bằng 2 và cạnh bên bằng 2 suy ra diện tích một mặt bên là: √3. Vậy S = 4√3+4. Vậy chọn A.
Bài 10 (trang 126 sgk Hình Học 12 nâng cao):
Một hình nón có đường sinh bằng l và bằng đường kính đáy. Trong các số sau đây, só nào là bán kính cầu nội tiếp hình nón?
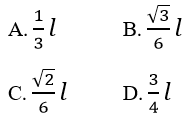
Lời giải:
Bán kính mặt cầu nội tiêp hình nón chính là bằng bán kính đường tròn nội tiếp tam giác đều cạnh l, ta tính được r = √3l/6 .
Vậy chọn B.
Bài 11 (trang 126 sgk Hình Học 12 nâng cao):
Một hình cầu có thể tích 4 π/3 nội tiệp một hình lập Phương. Thể tích của hình lập Phương đó bằng:
A. 8 B. 4 π C. 1 D. 2 π√3
Lời giải:
Vì thể tích mẳ cầu là:
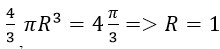
Vậy chọn A.
Bài 12 (trang 126 sgk Hình Học 12 nâng cao):
Cho hình chữ nhật có tọa độ hai đỉnh A(-2; 3; 0); B(2; 3; 0) và một cạnh nằm trên trục Ox. Khối tròn xoay sinh bởi hình chữ nhật đó khi quay quanh trục Oy có thể tích là:
A. 6 π2 B. 4 π C. 12 π D. 2 π√3
Lời giải:
Chọn C
Bài 13 (trang 126 sgk Hình Học 12 nâng cao):
Cho vectơ u→(1;0;2) và X→(0; -1;1). Trong các vectơ sau, vectơ nào cùng phương với [u→,v→ ]
A. a→(1;1;1) B.b→(-2;1;1)
C. c→(0;1;-1) D. d→(2;2; -1)
Lời giải:
Ta có [ u→,v→] cùng phương với b→(-2;1;1).
Vậy chọn B
Bài 14 (trang 127 sgk Hình Học 12 nâng cao):
Cho tam giác ABC có diện tích bằng 6 nằm trong mặt phẳng (α) có Phương trình 2x-2y+z+5=0. Thể tích hình chóp S.ABC với S = (1; 1; 1) bằng:
A. 3√6 B. 12√2 C. 8 D. 4
Lời giải:
Thể tích hình chóp S.ABC là:
![]()

Bài 15 (trang 127 sgk Hình Học 12 nâng cao):
Mặt cầu có tâm I(6; 3; -4) tiếp xúc với Ox có bán kính là:
A. 5 B. 2√3 C. 4√3 D. 4
Lời giải:
Bán kính mặt cầu là
![]()
Vậy chọn A
Bài 16 (trang 127 sgk Hình Học 12 nâng cao):
Cho đường thẳng d có phương trình
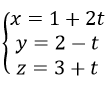
Phương trình tham số nào sau đây cũng là phương trình của d?
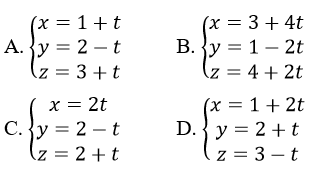
Lời giải:
Đường thẳng d có vecơ chỉ phương là u→=(2; -1;1) và d đi qua các điểm M có tọa độ dạng M – (1+2t; 2-t; 3+t), ∀t với t = 1 ta có tọa độ M = (3; 1; 4) ∈ d.
Vậy ta chọn B.
Bài 17 (trang 127 sgk Hình Học 12 nâng cao):
Cho hai đường thẳng d:
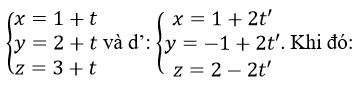
A. d cắt d’ B. d trùng d’
C. d và d’ chéo nhau D. d song song với d’
Lời giải:
Đường thẳng d đi qua M(1; 2; 3) có vectơ chỉ phương u ⃗(1;1; -1)
d’ đi qua M’(1; -1; 2) có vectơ chỉ phương u’→(2;2; -2)
ta thấy u→,u’→ cùng phương nhưng không cùng phương với vectơ MM’→=(0; -3; -1) nên d và d’ song song với nhau.
Vậy chọn D.
Bài 18 (trang 127 sgk Hình Học 12 nâng cao):
Cho mặt phẳng (P): 3x+4z+12=0 và mặt cầu (S): x2+y2+(z-2)2=1. Khi đó:
A. mp(P) đi qua tâm mặt cầu (S).
B. mp(P) tiếp xúc với mặt cầu (S).
C. mp(P) cắt (S) theo một đường tròn.
D. mp(P) không cắt (S).
Lời giải:
Mặt cầu (S) có tâm I(0; 0; 2) có bán kính R = 1.
Ta có
![]()
Vậy (P) không có điểm chung với (S). ta chọn D.
Bài 19 (trang 128 sgk Hình Học 12 nâng cao):
Tọa độ hình chiếu vuông góc của điểm M(2; 0; 1) trên đường thẳng:
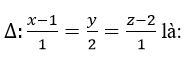
A. (1; 0; 2) B (2; 2; 3) C(0; -2; 1) D. (-1; 4; 0)
Lời giải:
Hình chiếu vuông góc của điểm M(2; 0; 1) trên đường thẳng
![]()
là giao điểm của mặt phẳng (α) đi qua M và (α)⊥Δ mp(α) có Phương trình: x+2y+z-3=0
Từ đó ta tìm được giao điểm của Δ với α là H(1; 0; 2).
Vậy chọn A.
Bài 20 (trang 128 sgk Hình Học 12 nâng cao):
Cho đường thẳng d:
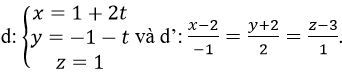
Khoảng cách giữa d và d’ là:

Lời giải:
Đường thẳng d đi qua M(1; -1; 1) và có vectơ chỉ phương u→(2; -1;0) d’ đi qua M’(2; -2; 3) và có vectơ chỉ phương u’→(-1;2;1)
Khoảng cách giữa d và d’ là:

Vậy chọn B
Bài 21 (trang 128 sgk Hình Học 12 nâng cao):
Cho đường thẳng

Phương trình đường thẳng vuông góc chung của d và d’ là:
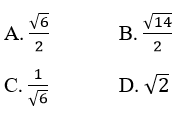
Lời giải:
Đường vuông góc chung của

là đường thẳng

Vậy chọn D.
Bài 22 (trang 128 sgk Hình Học 12 nâng cao):
Cho mặt phẳng (P): mx+y+(n-2)z+m+2=0. Với mọi m, n mặt phẳng (P) đi qua điểm cố định:
A. (1; 2; 0) B. (2; 1; 0) C. (0; 1; -2) D. (-1; -2; 0)
Lời giải:
Gọi M0(x0,y0,z0) là điểm cố định của mp(P)
Khi đó: mx0+y0+(n-2) z0+m+2=0 đúng với ∀m,n
<=> m(x0+1)+y0+nz_0-2z0+2=0 đúng với ∀m,n
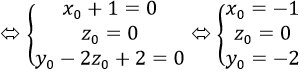
=> M0(-1;2; -2)
Vậy chọn D
Bài 23 (trang 129 sgk Hình Học 12 nâng cao):
Cho mặt cầu (S): x2+y2+z2-2x-4y-4z=0. Mặt phẳng tiếp xúc với (S) tại điểm A(3; 4; 3) có phương trình là:
A. 4x+4y-2z-17=0 B. 2x+2y+z-17=0
C. 2x+4y+z-17=0 D. x+y+z-17=0
Lời giải:
Mặt cầu (S): x2+y2+z2-2z-4y-4z=0 có tâm I(1; 2; 2) và có bán kính R = 3. Mặt phẳng (α) tiếp xúc với S tại A(3; 4; 3).
Khi A ∈(α) và d(I,α)=R=3
Ta thấy mp: 2x+2y+z-17=0 thỏa mãn hai điều kiện trên, vậy chọn B.