Bài 1 (trang 45 sgk Hình Học 12 nâng cao):
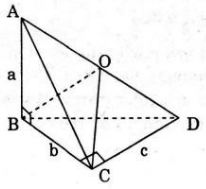
Trong không gian cho ba đoạn thẳng AB, BC, CD sao cho AB ⊥ BC, BC ⊥ CD, CD⊥AB. Chứng minh rằng có mặt cầu đi qua bốn điểm A, B, C, D. tính bán kính mặt cầu nếu AB = a, BC = b, CD = c.
Lời giải:

Vì AB⊥BC VÀ AB⊥CD nên AB⊥BD
Tương tự ta có: DC⊥AC
Theo tính chất đường trung tuyến của tam giác vuông ứng với cạnh huyền: BO = CO = 1/2 AD. Suy ra A, B, C, D nằm trên mặt cầu tâm O,
Tâm mặt cầu O là trung điểm của AD
Bài 2 (trang 45 sgk Hình Học 12 nâng cao):
a) Tìm tập hợp các mặt cầu đi qua hai điểm phân biệt A, B cho trước.
b) Tìm tập hợp tam các mặt cầu đi qua đường tròn cho trước.
c) Có hay không một mặt cầu đi qua một đường tròn và một điểm nằm ngòi mặt phẳng của đường tròn.
Lời giải:
a) Gọi I là tam mặt cầu đi qua điểm A, B cho trước, khi đó IA = IB. vậy I nằm trên mặt phẳng trung trực của AB.
b) I là tâm mặt mầu đi qua ba điểm A, B, C cho trước và khi và chỉ khỉ IA = IB = IC. Vậy:
+ Nếu ba điểm A, B, C không thẳng hàng thì tập hợp các điểm I là trung trực của đường tròn ngoại tuyến tam giác ABC.
+ nếu ba điểm A, B, C thăng hàng và đôi một phân biệt thì tập hợp các điểm I là trục trực của của đường tròn ngoại tiếp tam giác ABC.
c) I là tâm mặt cầu đi qua đường tròn (C) cho trước khi và chỉ khi I cách đều mọi điểm của đường tròn. Vậy tập hợp các điểm I là trung trực của đường tròn (C )
d) Gọi M là trung điểm nằm ngoài mặt phẳng của đường tròn C. lấy điểm A nằm trên (C) và gọi I là giao điểm của trung trực đường tròn và mặt phẳng trung trực của MA. Khi đó mặt cầu tâm I, bán kính R = IA = IM là mặt cầu tâm I, bán kính R = IA = IM là mặt cầu đi qua đường tròn C và đi qua điểm M.
Bài 3 (trang 45 sgk Hình Học 12 nâng cao):
Cho điểm M nằm trong mặt cầu (S). Trong các mệnh đề sau mệnh đề nào đúng?
a) Mọi mặt phẳng đi qua M đều cắt (S) theo một đường tròn.
b) Mọi đường thẳng qua M đều cắt (S) tại hai điểm phân biệt.
Lời giải:
Cả a, b đều đúng.
Bài 4 (trang 45 sgk Hình Học 12 nâng cao):
Cho đường thẳng d và điểm A không nằm trên d. xét các mặt cầu đi qua A và có tâm nằm trên d, chứng minh rằng các mặt cầu đó luôn luôn đi qua một đường tròn cố định.
Lời giải:
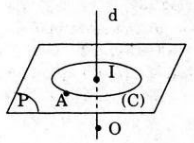
Gọi S là mặt cầu đi qua điểm A có tâm O nằm trên d (hình vẽ bên). Gọi (P) là mặt phẳng đi qua A và vuông góc với d. khi đó (P) cắt mặt cầu (S) theo giao tuyến đường tròn (C), có tâm I là giao của mặt phẳng (P) với d, bán kính r = IA => (C) cố định.
Bài 5 (trang 45 sgk Hình Học 12 nâng cao):
Cho mặt cầu cố định (C).
Mệnh đề nào sau đây là đúng?
a) Mọi mặt của nó là đa giác nên mặt cầu thì mọi mặt của nó là đa giác nội.
b) Đường tròn thì đa diện đó nội tiến nội tiếp đường trong thì đa diện đó nội tiếp.
Lời giải:
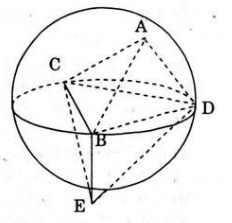
ABCD nội tiếp tại điểm E nằm trong mặt phẳng (BCD). Có 6 mặt ABC, các mặt đều là hình đa diện cầu. vì nếu có C, D, E thì nó là hình cấu đó chính là tiếp diện trên S.
Bài 7 (trang 45 sgk Hình Học 12 nâng cao):
a) Tính thể tích khối cầu ngoài tiếp hình bằng a và chiều cao h.
b) Cho hình chóp tứ giác đều S.ABCD có . Gọi A’, B’, C’ D’ lần lượt là csac trung điểm của A, B, C, D. tính thể tích khối cầu đó.
Lời giải:
a) Giả sử SH là đường cao của hình chóp đều S.ABC. khi đó SA SB = SC nên mọi điểm nằm trên SH cách đều A, B, C.
Trong mặt phẳng (SAH) đường trung trực của SA cắt SH tại O là tâm mặt cầu ngoại tiếp hình chóp, bán kính cầu là R = SO.
Gọi I là trung điểm SA thì tứ giác AHOI nội tiếp.
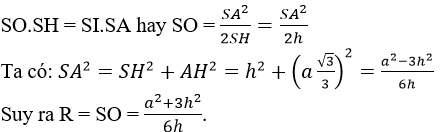
b)Gọi SH là đường cao của hình chóp đều SABCD thì H là tâm hình vuông ABCD và SH đi qua tâm H’ của hình vuông A’B’C’D’. hình vẽ. Mọi điểm nằm trên SH và cách đều 4 điểm A, B, C, D và cũng là cách đều 4 điểm A’, B’, C’, D’. trên SH xác định điểm O sao cho OA = OA’ thì O các ddefu 8 đỉnh A, B, C, D, A’, B’, C’, D’ tức 8 đỉnh đó nằm trên mặt cầu tâm O, bán kính R = OA. Điểm O là giao điểm của đương thẳng SH và mặt phẳng trung trực của đoạn AA’.
Do ΔSAC cân tại S. Gọi I là trung điểm của AA’ thì ΔSIO cũng vuông cân tại I nên IO = SI = 3a/4. Suy ra:
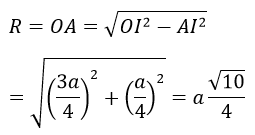
Thể tích khối cầu là:
![]()
Bài 8 (trang 45 sgk Hình Học 12 nâng cao):
Cho tứ diện ABCD, với AB= CD = c, AC = BD = b, AD = BC = a.
a) Tính diện tích mặt cầu ngoại tiếp tứ diện.
b) Chứng minh rằng có một mặt cầu tiếp xức với bốn mặt cầu tư diện (nó được gọi là mặt cầu nội tiếp tứ diện).
Lời giải:
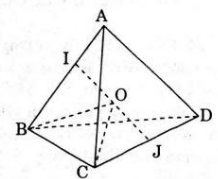
a) Gọi I, J lần lượt là trung điểm của AB và CD thì IJ ⊥ AB, IJ ⊥ Cd
Gọi O là trung điểm của IJ thì OA = OB và OC = OD.
Do AB = CD = c nên hai tam giác vuông OIB và OJC bằng nahu nên OB = Oc.
Vậy O cách đều 4 đỉnh A, B, C, D
Mặt cầu ngoại tiếp tứ diện ABCD có tâm O, bán kính R = OA.
Ta có:
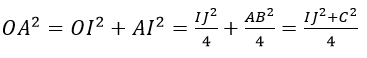
Vì CI là trung tuyến của tam giác ABC nên.
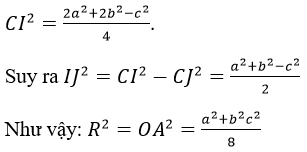
diện tích mặt cầu ngoại tiếp tứ diện ABCD là
![]()
b) Các mặt của tứ diện là tam giác bằng nhau (đều có ba cạnh là a, b, c) nên các đường tròn ngoại tiếp các tam giác đó có bán kính r bằng nhau. Các đường tròn đó đều nằm trên mặt cầu (O, R) nên khoảng cách từ tâm O tới các mặt phẳng chứa các đường tròn đó bằng nhau và bằng
![]()
Vậy mặt cầu tâm O bán kính h là mặt cầu nội tiếp tứ diện ABCD.
Bài 9 (trang 46 sgk Hình Học 12 nâng cao):
Tìm diện tích mặt cầu ngoại tiếp hình chóp SABC biết SA = a, SB = b, SC = c và ba cạnh Sa, SB, SC đôi một vuông góc. Chứng minh rằng các điểm S, G, I thẳng hàng, trong đó G là trọng tâm tam giác ABC và I là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
Lời giải:
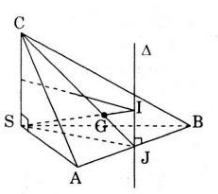
Gọi J là trung điểm của AB. Vì tam giác SAB vuông ở đỉnh S nên Í = JA = IB (hình vẽ bên)
Gọi Δ là đường thẳng vuông góc với mặt phẳng (SAB) tại J thì mọi điểm của đường Δ đều cách 3 điểm S, A, B. Bởi vậy nếu gọi I là giao điểm của Δ với mặt phẳng trung trực của đoạn SC thì I các đều 4 điểm S, A, B, C.
Vậy mặt cầu ngoại tiếp hình chóp có tâm I, bán kính R = IA.
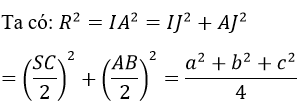
Diện tích mặt cầu bằng: S = 4πR2=π(a2+b2 + c2)
Vì (SC // IJ nên SI cắt CJ tại điểm G và do SC = 2IJ nên CG = 2GJ. Do CJ là trung tuyến của tam giác ABC nên G là trọng tâm tam giác ABC.
Bài 10 (trang 46 sgk Hình Học 12 nâng cao):
a) Chứng minh rằng một hình lăng trụ có mặt cầu ngoại tiếp khi và chỉ khi nó là hình lăng trụ đứng và đáy là đa giác nội tiếp đường tròn.
b) Trong các hình hộp nội tiếp mặt cầu cho trước, hình hộp nào có diện tích toàn phần lớn nhất.
Lời giải:
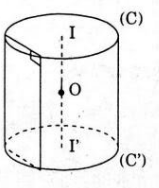
a) Nếu H là hình lăng trụ có mặt cầu ngoại tiếp thì các mặt bên là những hình bình hành có đường tròn ngoại tiếp nen phải là hình chữ nhật. ngoài ra H có mặt cầu ngoại tiếp nên mặt đáy phải là đa giác có đường tròn ngoại tiếp.
Ngược lại cho H là lăng trụ đúng có các đường tròn C và C’ ngoại tiếp các đa giác (hình vẽ).
Gọi I, I’ là tâm của C và C’ thì II’ là trục của cả hai đường tròn, gọi O là trung điểm của II’ thì cách đều tấu cả các đỉnh của hình lăng trụ đa cho.
Vậy hình lăng trụ ấy có mặt cầu ngoại tiếp.
b) Nếu hình hộp H nội tiếp mặt cầu S(O, R) thì các mặt của H phải là những hình chữ nhật, vậy H là hình chữ nhật mà O là các giao điểm các đường chéo, và độ dài đường chéo d = 2R.
Gọi a, b, c là các kích thước của hình hộp chữ nhật đó thì a2+b2+c2=d2=4R2. Gọi S là diện tích toàn phần của hình hộp thì ta có:
S = 2ab +2bc + 2ac ≤2(a2+b2+c2 )=8R2.
Vậy S đạt giá trị lớn nhất bằng 8R2 thì
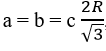
tức là H là hình lập phương.
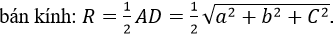
3wallace
popular gay chat 360 https://bjsgaychatroom.info/
gay dating apps described https://gaypridee.com/
ffree gay chat https://gay-buddies.com/
princess bride slots https://freeonlneslotmachine.com/
slots of vegas casino https://pennyslotmachines.org/
free fun slots no download https://slotmachinesworld.com/
how to win at slots https://beat-slot-machines.com/
casino gem slots https://411slotmachine.com/
casino slots free https://www-slotmachines.com/
vegasworld fun free slots https://slotmachinegameinfo.com/
writing dissertation tips https://dissertationwriting-service.com/
dissertation assistance https://dissertations-writing.org/
Comments are closed.