[Giải Toán 10] Chương 3: Phương pháp tọa độ trong mặt phẳng/ Bài 1: Phương trình đường thẳng

Bài 1: Phương trình đường thẳng

Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 70: Trong mặt phẳng Oxy cho đường thẳng  là đồ thị của hàm số: y = 1/2x.

a) Tìm tung độ của hai điểm M_o và M nằm trên Δ, có hoành độ lần lượt là 2 và 6.

b) Cho vectơ u→ = (2; 1). Hãy chứng tỏ M_oM→ cùng phương với u ⃗.

Lời giải

a) Với x = 2 ⇒ y = 1/2 x = 1 ⇒ M_o (2;1)

x = 6 ⇒ y = 1/2 x = 3 ⇒ M_o (6;3)

b) M_oM→ = (4;2) = 2(2;1) = 2u→

Vậy M_oM→ cùng phương với u

Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 71: Hãy tìm một điểm có tọa độ xác định và một vectơ chỉ phương của đường thẳng có phương trình tham số

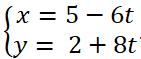
Lời giải

Một điểm thuộc đường thẳng là (5; 2)

Một vecto chỉ phương là u→ (-6;8)

Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 72: Tính hệ số góc của đường thẳng d có vectơ chỉ phương là u→ = (-1; √3).

Lời giải

Hệ số góc của đường thẳng d có vectơ chỉ phương u→ = (-1; √3) là:

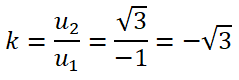
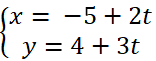
Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 73: Cho đường thẳng Δ có phương trình và vectơ n→ = (3; -2). Hãy chứng tỏ n ⃗ vuông góc với vectơ chỉ phương của Δ.

Lời giải

Vectơ chỉ phương của Δ là: u→ = (2;3)

n→.u→ = 3.2 + (-2).3 = 6 – 6 = 0

Vậy n→ vuông góc với vectơ chỉ phương của Δ.

Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 74: Hãy chứng minh nhận xét trên.

Lời giải

Chọn N(0; -c/b); M(-c/a;0) thuộc đường thẳng Δ.

⇒MN→ =(c/a; (-c)/b)

Ta thấy n→.MN→ = 0

Vậy n→ = (a;b) là vecto pháp tuyến của đường thẳng.

n→.u→ = a.b – b.a = 0 nên u→ (-b;a) là vecto chỉ phương của đường thẳng.

Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 74: Hãy tìm tọa độ của vectơ chỉ phương của đường thẳng có phương trình: 3x + 4y + 5 = 0.

Lời giải

Vecto pháp tuyến của đường thẳng làn→ = (3;4)

⇒ Vecto chỉ phương của đường thẳng là u→ (-4;3).

Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 76: Trong mặt phẳng Oxy, hãy vẽ các đường thẳng có phương trình sau đây:

d₁: x – 2y = 0;

d₂: x = 2;

d₃: y + 1 = 0;

d₄: x/8 + y/4 = 1.

Lời giải

Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 77: Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:

d₁: -3x + 6y – 3 = 0;

d₂: y = -2x;

d₃: 2x + 5 = 4y.

Lời giải

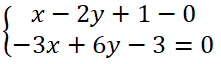
Xét Δ và d₁, hệ phương trình: có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d₁.

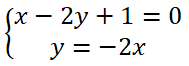
Xét Δ và d₂, hệ phương trình: có nghiệm duy nhất (-1/5; 2/5) nên

Δ cắt d₂ tại điểm M(-1/5; 2/5).

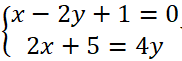
Xét Δ và d₂, hệ phương trình: vô nghiệm

Vậy Δ // d₂

Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 78: Cho hình chữ nhật ABCD có tâm I và cạnh AB = 1, AD = √3. Tính số đo các góc ∠(AID) và ∠(DIC) .

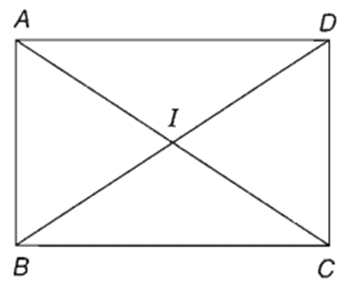
Lời giải

Xét ΔABD vuông tại A có:

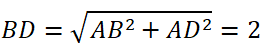
Do ABCD là hình chữ nhật tâm I nên:

AI = IC = ID = 1/2 BD = 1

ΔICD có ID = IC = DC = 1

⇒ΔICD đều ⇒ ∠(DIC) = ∠(IDC) = 60^o

Ta có: ∠(IDC) + ∠(AID ) = 180^o⇒ ∠(AID ) = 180^o– 60^o= 120^o

Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 80: Tính khoảng cách từ các điểm M(-2; 1) và O(0; 0) đến đường thẳng Δ có phương trình 3x – 2y = 0.

Lời giải

Khoảng cách từ điểm M (-2; 1) đến đường thẳng Δ là:

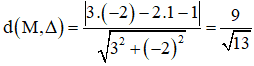
Khoảng cách từ điểm O (0; 0) đến đường thẳng Δ là:

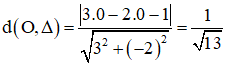
Bài 1 (trang 80 SGK Hình học 10): Lập phương trình tham số của đường thằng d trong mỗi trường hợp sau:

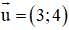
a) d đi qua điểm M(2; 1) và có vec tơ chỉ phương ;

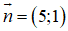
b) d đi qua điểm M(–2; 3) và có vec tơ pháp tuyến .

Lời giải

a) Phương trình tham số của d là:

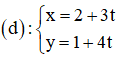
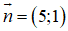
b) d nhận là 1 vec tơ pháp tuyến

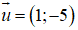
⇒ d nhận là 1 vec tơ chỉ phương

Phương trình tham số của đường thẳng d là:

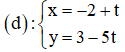
Kiến thức áp dụng

– Các định nghĩa

+ Vec tơ chỉ phương của một đường thẳng là vec tơ có giá song song hoặc trùng với đường thẳng đó, thường được kí hiệu là vec tơ u→.

+ Vec tơ pháp tuyến là vec tơ có giá vuông góc với đường thẳng đó, thường được kí hiệu là vec tơ n→.

+ Một đường thẳng có vô số vec tơ chỉ phương và vec tơ pháp tuyến.

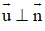
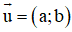
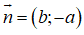
+ Ta luôn có : . Do đó nếu biết thì ta thường chọn và ngược lại.

– Để viết phương trình tham số của một đường thẳng ta cần :

+ Tìm một điểm M(x₀; y₀) nằm trên đường thẳng .

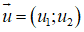
+ Tìm 1 vec tơ chỉ phương

Khi đó phương trình tham số của đường thẳng là:

Comments

comments