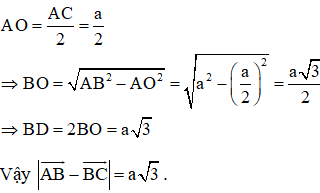Trả lời câu hỏi Toán 10 Hình học Bài 2 trang 9: Hãy kiểm tra các tính chất của phép cộng trên hình 1.8.
Lời giải
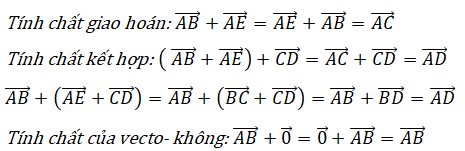
Trả lời câu hỏi Toán 10 Hình học Bài 2 trang 10: Vẽ hình bình hành ABCD. Hãy nhận xét về độ dài và hướng của hai vectơ AB→ và CD→.
Lời giải
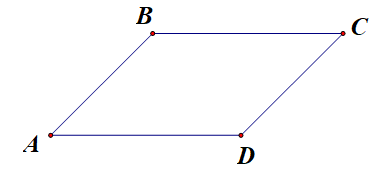
Về độ dài: hai vectơ AB→ và CD→ có cùng độ dài
Về hướng: hai vectơ AB→ và CD→ có hướng ngược nhau.
Trả lời câu hỏi Toán 10 Hình học Bài 2 trang 10: Cho AB→ + BC→ = 0→. Hãy chứng tỏ BC→ là vectơ đối của AB→.
Lời giải
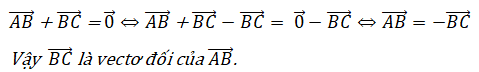
Trả lời câu hỏi Toán 10 Hình học Bài 2 trang 11: Hãy giải thích vì sao hiệu của hai vectơ OB→ và OA→ là vectơ AB→.
Lời giải
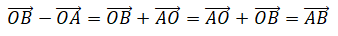
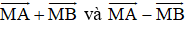
Bài 1 (trang 12 SGK Hình học 10): Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho AM > MB. Vẽ các vector
Lời giải:
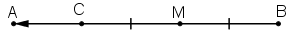
– Trên đoạn MA, lấy điểm C sao cho MC = MB
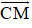
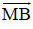
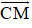
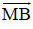
Nhận thấy và cùng hướng nên =
Khi đó:
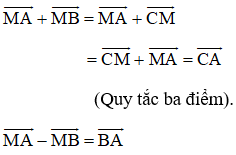
Kiến thức áp dụng
+ Quy tắc ba điểm : Với ba điểm A, B, C bất kì ta có:
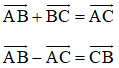
Bài 2 (trang 12 SGK Hình học 10): Cho hình bình hành ABCD và điểm M tùy ý. Chứng minh rằng
Lời giải:
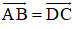
Ta có: ABCD là hình bình hành nên
Kiến thức áp dụng
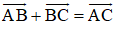
+ Quy tắc ba điểm: với mọi điểm A, B, C.
+ a→ + 0→ = a→
Bài 3 (trang 12 SGK Hình học 10): Chứng minh rằng đối với tứ giác ABCD bất kỳ ta luôn có:
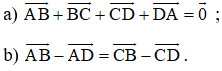
Lời giải:
a) Ta có:
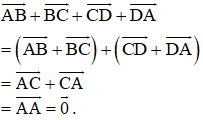
b) Áp dụng quy tắc trừ hai vec tơ ta có:
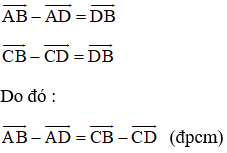
Kiến thức áp dụng
+ Quy tắc ba điểm : Với A, B, C bất kì ta có :
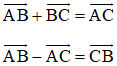
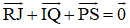
Bài 4 (trang 12 SGK Hình học 10): Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành: ABIJ, BCPQ, CARS. Chứng minh rằng
Lời giải:
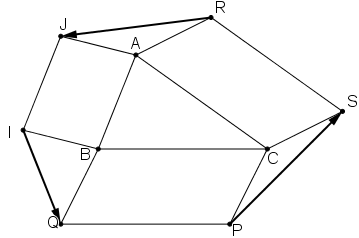
Ta có:
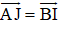
AJIB là hình bình hành nên
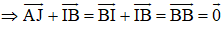
Tương tự như vậy:
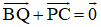
BCPQ là hình bình hành nên
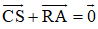
CARS là hình bình hành nên
Do đó:
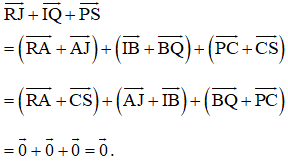
Kiến thức áp dụng
Quy tắc ba điểm cộng hai vec tơ
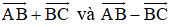
Bài 5 (trang 12 SGK Hình học 10): Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ
Lời giải:
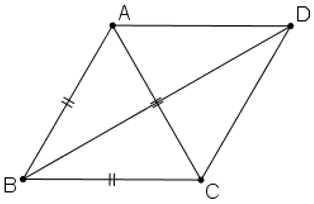
Ta có:
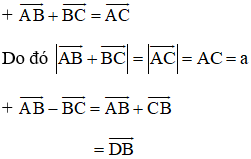
(Quy tắc hình bình hành)
(Trong đó D là đỉnh còn lại của hình bình hành ABCD)
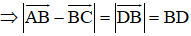
+ Tính BD:
Hình bình hành ABCD có AB = BC = a nên ABCD là hình thoi.
⇒ AC ⊥ BD tại O là trung điểm của AC và BD.
