Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 4: Với hai điểm A, B phân biệt ta có được bao nhiêu vectơ có điểm đầu và điểm cuối là A hoặc B.
Lời giải
Với hai điểm A, B phân biệt ta có được 2 vectơ có điểm đầu và điểm cuối là A hoặc B
Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 5: Hãy nhận xét về vị trí tương đối của các giá của các cặp vectơ sau:
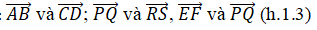
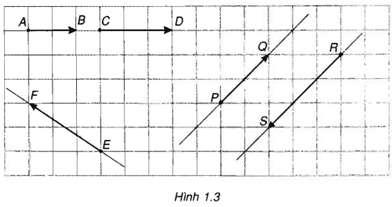
Lời giải

Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 6: Khẳng định sau đúng hay sai:
Nếu ba điểm phân biệt A, B, C thẳng hàng thì hai vectơ (AB→ và BC→ cùng hướng.
Lời giải
Khẳng định trên sai, chúng chỉ cùng phương, không cùng hướng.
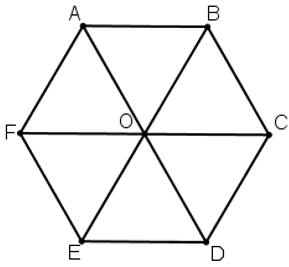
Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 6: Gọi O là tâm hình lục giác đều ABCDEF. Hãy chỉ ra các vectơ bằng vectơ OA→
Lời giải

Vectơ bằng vectơ OA→ là vectơ DO→
Bài 1 (trang 7 SGK Hình học 10): Cho ba vectơ a→, b→, c→ đều khác vectơ . Các khẳng định sau đúng hay sai?
a) Nếu hai vec tơ a→, b→ cùng phương với c→ thì a→ và b→ cùng phương.
b) Nếu a→, b→ cùng ngược hướng với c→ thì a→ và b→ cùng hướng.
Lời giải:
a) Gọi Δ1, Δ2, Δ3 lần lượt là giá của ba vectơ a→, b→, c→
+ Vectơ a cùng phương với vectơ c ⇒ Δ1 //≡ Δ3
+ Vectơ b cùng phương với vectơ c ⇒ Δ2 //≡ Δ3
⇒ Δ1 //≡ Δ2
⇒ Vectơ a→ cùng phương với b→ (theo định nghĩa).
b) a→, b→ cùng ngược hướng với c→
⇒ a→, b→ đều cùng phương với c→
⇒ a→ và b→ cùng phương.
⇒ a→ và b→ chỉ có thể cùng hướng hoặc ngược hướng.
Mà a→ và b→ đều ngược hướng với c→ nên a→ và b→ cùng hướng.
Kiến thức áp dụng
Hai vec tơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Hai vec tơ cùng phương thì chỉ có thể cùng hướng hoặc ngược hướng.
Bài 2 (trang 7 SGK Hình học 10): Trong hình 1.4, hãy chỉ ra các vectơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau.

Lời giải:
– Các vectơ cùng phương:
a→ và b→ cùng phương
u→ và v→ cùng phương
x→, y→, w→ và z→ cùng phương.
– Các vectơ cùng hướng:
a→ và b→ cùng hướng
x→, y→ và z→ cùng hướng
– Các vectơ ngược hướng:
u→ và v→ ngược hướng
w→ ngược hướng với các vec tơ x→, y→ và z→
– Các vectơ bằng nhau: x→ = y→
Kiến thức áp dụng
+ Hai vec tơ cùng phương là hai vec tơ có giá song song
+ Hai vec tơ cùng phương sẽ cùng hướng hoặc ngược hướng.
+ Hai vec tơ bằng nhau là hai vec tơ cùng hướng và có độ dài bằng nhau.
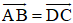
Bài 3 (trang 7 SGK Hình học 10): Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi
Lời giải:


Kiến thức áp dụng
Hai vec tơ bằng nhau nếu chúng cùng hướng và có độ dài bằng nhau.
Bài 4 (trang 7 SGK Hình học 10): Cho lục giác đều ABCDEF có tâm O.
a) Tìm các vectơ khác vectơ O→ và cùng phương với vectơ OA→.
b) Tìm các vectơ bằng vectơ AB→.
Lời giải:
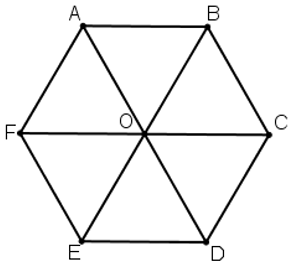
a) Các vectơ khác vectơ O→ và cùng phương với vectơ OA→ là:
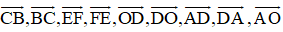
b) Các vectơ bằng vectơ AB→ là:
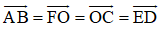
Kiến thức áp dụng
+ Hai vec tơ cùng phương là hai vec tơ có giá song song với nhau hoặc trùng nhau
+ Hai vec tơ bằng nhau là hai vec tơ có cùng hướng và có độ dài bằng nhau.