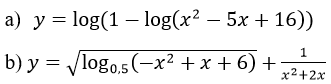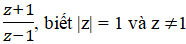
Bài 1 (trang 211 sgk Giải Tích 12 nâng cao):
a) Chứng minh rằng hàm số f(x) = e2-x-1 đồng biến trên nửa khoảng [0; +∞)
b) Từ đó suy ra ex>x+1 với mọi x > 0
Lời giải:
a) Ta có: f’(x) = (ex-x-1)’=ex-1
f’ (x)≥0 <=> ex-1≥0 <=> ex≥1 <=> x ≥0
Vậy f(x) đồng biến trên [0; +∞)
b) Vì f(x) = ex-x-1 đồng biến trên [0; +∞) nên:
f(x)>f(0)với mọi x > 0, mà f(0) = 0 nên ta có:
f(x)>0 <=> ex-x-1>0 <=> ex>x+1 (đpcm)
Bài 2 (trang 211 sgk Giải Tích 12 nâng cao):
a) Khảo sát và vẽ đồ thị hàm số f(x) =2x3-3x2-12x-10=0
b) Chứng minh rằng Phương trình 2x3-3x2-12x-10=0 có nghiệm thực duy nhất.
c) Gọi nghiệm duy nhất của Phương trình là α.
Chứng minh rằng: 3,5<α<3,6
Lời giải:
a) Tập xác định: R
f’ (z)=6x2-6x-12;f(x)=0 <=> x=-2 ;x=2
f” (x)=12x-6;f” (x)=0 <=> x=1/2
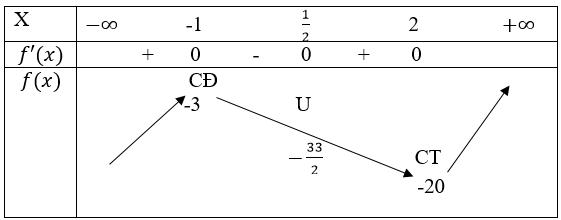
Bảng biến thiên

Đồ thị
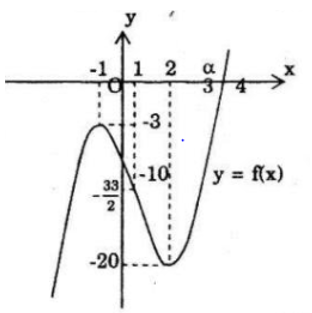
b) Nhìn vào đồ thị của hàm số y = 2x3-3x2-12x-10=0 ta thấy đồ thị chỉ cắt Ox tại 1 điểm duy nhất, nên phương trình:
2x3-3x2-12x-10=0 có 1 nghiệm duy nhất.
c) Xét f(x) = 2x3-3x2-12x-10. Ta có f(3; 5); f(3; 6) < 0 mà f(x) là hàm liên tục nên f(x) có một nghiệm α ∈(3,5;3,6)(đpcm)
Bài 3 (trang 211 sgk Giải Tích 12 nâng cao):
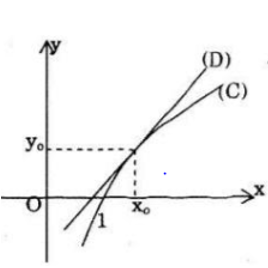
Gọi C là đồ thị hàm số của y = lnx và D là một tiếp tuyến bất kì của C. chứng minh rằng trên (0; +∞), C nằm ở phía dưới của đường thẳng D.
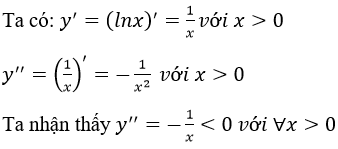
nên đồ thị hàm số y = lnx lồi trên (0; +∞) nên đường tiếp tuyến D luôn nằm trên đồ thị C. (đpcm)
Lời giải:
Bài 4 (trang 212 sgk Giải Tích 12 nâng cao):
Một xưởng in có 8 máy in, mỗi máy in được 3600 bản trong một giờ. Chi phí để vận hành một trong mỗi lần là 50 nghìn đồng. chi phí cho n máy chạy trong một giờ là 10(6n +10) nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất.
Lời giải:
Giả sử dụng máy n máy để in (n = 1; 2; 3; 4; 5; 6; 7; 8)
Khi đó, tổng chi phí để in 50000 tờ quảng cáo là:
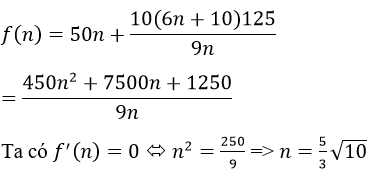
Bảng biến thiên của f(n)
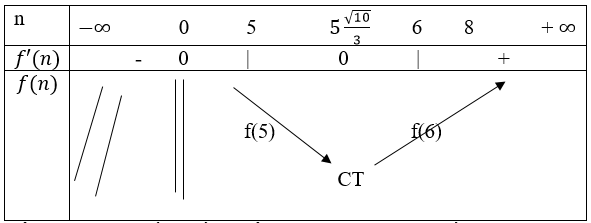
Để ta được lãi nhiều nhất thì tổng chi phí phải là ít nhất.
Vậy ta cần tìm n ∈{1;2;3;4;5;6;7;8} để f(n) nhỏ nhất. ta có f(5) < f(6), kết hợp với bảng biến thiên của f(n) thì khi n = 5 tổng chi phí sẽ bé nhất.
Vậy nên chọn 5 máy.
Bài 5 (trang 121 sgk Giải Tích 12 nâng cao): Tìm giá trị lớn nhất và nhỏ nhất của hàm số
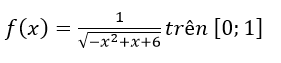
Lời giải:
Theo giả thiết ta có: logab=√3 => b = a√3
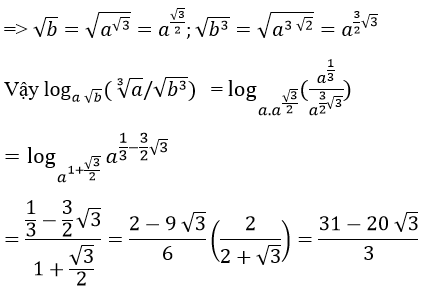
Bài 8 (trang 212 sgk Giải Tích 12 nâng cao):
a) Tính đạo hàm của các hàm số: y=cosx.e2tanx và y=log2(sinx)
b) Chứng minh rằng hàm số y=e4x+2.e-x thõa mãn hệ thức.
y”’-13y’-12y=0
Lời giải:
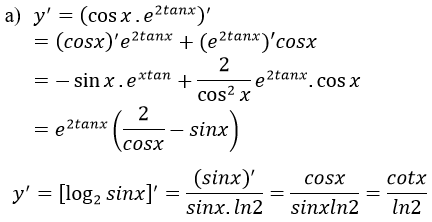
b) Ta có: y’=(e4x+2e-x=4e4x-2e-x
y”=(4e4x-2e-x )’=16e4x+2e-x
y”’=(4e4x-2e-x )’=64e4x-2e-x
Vậy y”’-13y’-12y=64e4x-2e-x-13(16e4x+2e-x )-12(4e4x-2e-x)
=64e4x-2e-x-52e4x+26e-x-12e4x-24e-x=0 (đpcm)
Bài 9 (trang 212 sgk Giải Tích 12 nâng cao):
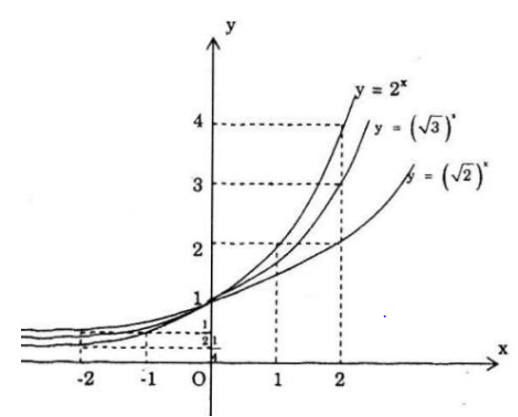
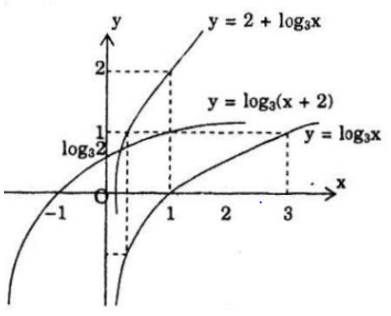
a) Vẽ đồ thị của hàm số y=2x,y=(√2)x;y=(√3)x trên cùng một mặt phẳng tọa độ. Hãy nhận xét vị trị tương đối của ba đồ thị.
b) Vẽ đồ thị y=log3x. Từ đó suy ra đồ thị của hàm số y=2+log3x và đồ thị của hàm số y=log3(x+2)
Lời giải:
a) Vẽ đồ thị các hàm số: y=2x,y=(√2)x;y=(√3)x
nhận xét:
Trong khoảng (-∞;0) đồ thị sắp xếp theo thứ tự từ trên xuống dưới là: ,y=(√2)x;y=(√3)x;y=2x
Đồ thị cả ba hàm số đi qua điểm (0; 1)
Khoảng (0; +∞) đồ thị sắp xếp theo thứ tự từ trên xuống dưới là:
y=2x,y=(√3)x;y=(√2)x
Như vậy “độ dốc” của đồ thị hàm số tăng theo giá trị cơ số:
√2<√3<2
b) Vẽ đồ thị hàm số y=log3x (C )
Đồ thị hàm số y = 2 + log3x có được bằng cách tịnh tiến (C) lên trên theo phương Oy 2 đơn vị.
Đồ thị hàm số y=log3x+2 có được bằng cách tính tiến (C) sang bên trái theo phương Ox 2 đơn vị.
Bài 10 (trang 212 sgk Giải Tích 12 nâng cao):
Giải các phương trình sau:
Lời giải:
a) Phương trình: 81sin2x + 81cos2x =30 <=> 81sin2x + 811-sin2x =30
Đặt t=81sin2x ,t>0, ta có Phương trình: t+81/t=30
<=> t2-30t+81=0 <=> t = 27; t = 3
Với t = 27 => 81sin2x =27 <=> 34 sin2x=33 <=> 4 sin2x=3
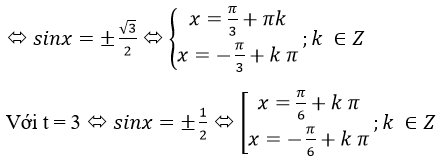
Vậy Phương trình đã cho có 4 họ nghiệm:
![]()
b) Đặt log1/2x=t với x > 0, ta có Phương trình.
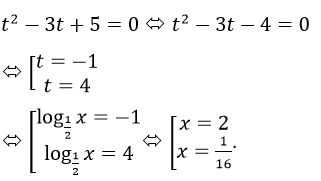
Vậy phương trình có hai nghiệm là x = 2; x = 1/16
c) Đặt logx=t ta có phương trình:
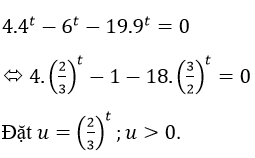
Ta có phương trình:
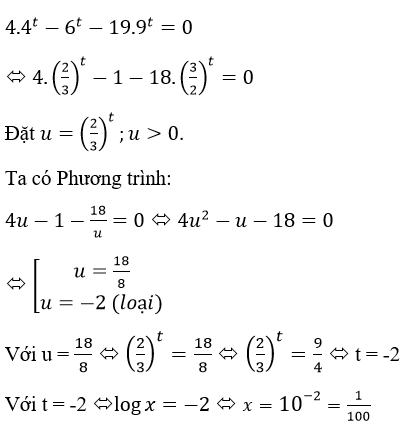
Vậy Phương trình có 1 nghiệm
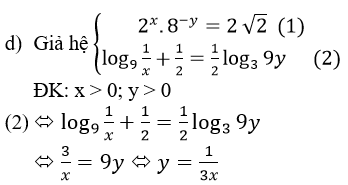
Thay y=1/3x vào (1) ta được.
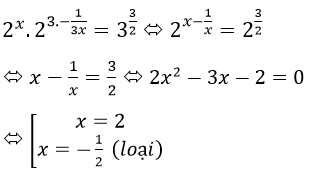
Với x = 2 => y=1/6. Vậy hệ có 1 nghiệm là
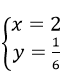
Bài 11 (trang 213 sgk Giải Tích 12 nâng cao): Tập hợp xác định của các hàm số sau:
Lời giải:
a) Hàm số y=log(1-log(x2-5x+16)) xác định khi:
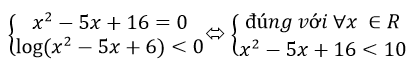
<=> x2-5x+6<0 <=> x ∈(2;3)
Vậy tập xác định của hàm số là khoảng (2; 3)
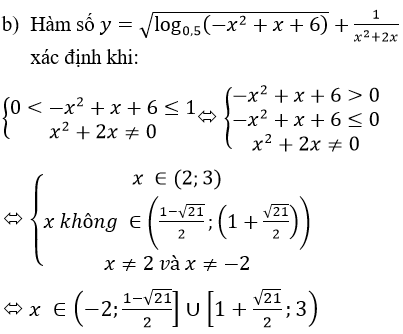
Bài 12 (trang 213 sgk Giải Tích 12 nâng cao):
Tìm họ nguyên hàm của mỗi hàm số sau trên khoảng xác định của nó.
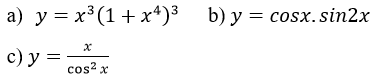
Lời giải:
a) Tìm F(x) = ∫x3(1+x4 )3. Đặt u=1+x4 => du = 4x3 dx
![]()
b) Tìm F(x) = ∫cosx.sin2x dx=2 ∫cos2x.sinxdx
Đặt cosx = u => -sinxdx=du. Ta có:
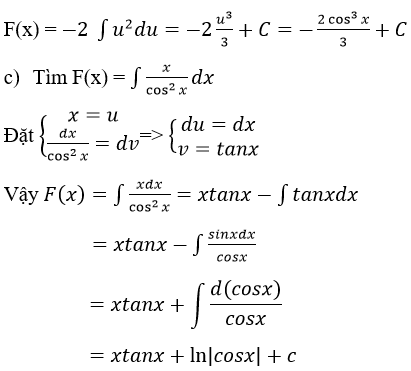
Bài 13 (trang 213 sgk Giải Tích 12 nâng cao): Tìm hàm số f(x) biết
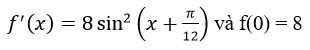
Lời giải:
Bài 14 (trang 213 sgk Giải Tích 12 nâng cao):
Tính các tích phân sau:
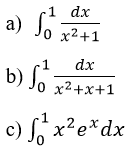
Lời giải:
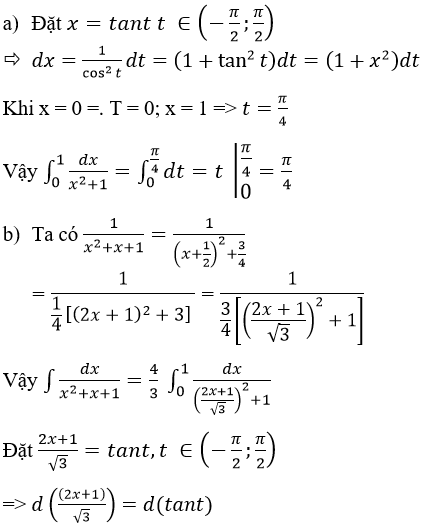
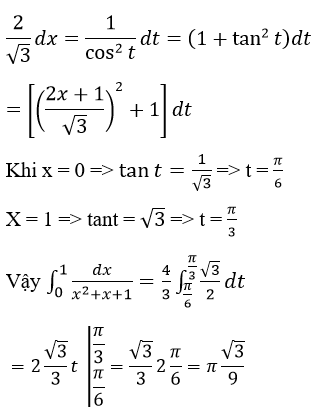
c) Theo công thức tích phân từng phần, ta có:
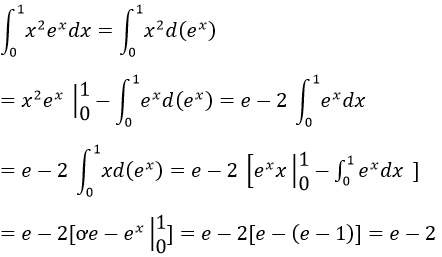
Bài 15 (trang 214 sgk Giải Tích 12 nâng cao):
Tính diệ tích hình phẳng giới hạn bởi các đường.
a) y+x2=0 và y+3x2=2
b) y2-4x=4 và 4x-y=16
Lời giải:
a) Hoành độ giao điểm của hai đường thẳng: y=-x2 và y=-3x2+2 là nghiệm của Phương trình: -x2=-3x2+2 <=> x2=1 <=> x=±1
Vậy diện tích cần tìm là:
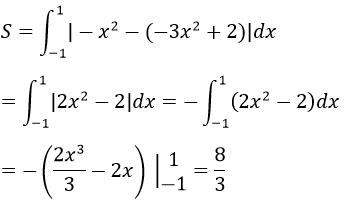
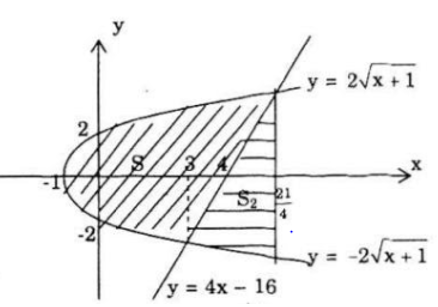
b) Diện tích cần tìm là S=S1-S2 (hình vẽ)
Hai đường đã cho cắt nhau tại hai điểm có hoành độ là 3 và 21/4
S1 là diện tích hình phẳn giới hạn bởi đường y2-4x-4=0 và đường thẳng x=21/4
Ta có:
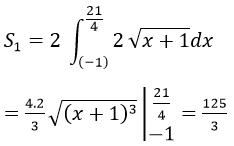
S2 là diện tích hình phẳng giới hạn bởi 3 đường: y2=4x+4;y=4x-16 và x=21/4
Ta có:
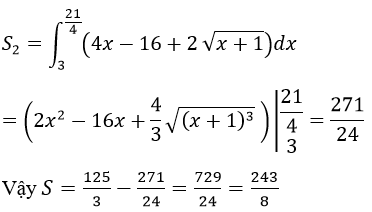
Bài 16 (trang 213 sgk Giải Tích 12 nâng cao):
a) Cho hình thang cong A giới hạn bởi đồ thị hàm số y=ex, trục hoành và các đường thẳng x = 0 và x = 1. Tính thể tích khối tròn xoay tạo được khi quay A quang trục hoành.
b) Cho hình phẳng B giới hạn bởi parabol y=x2+1 và đường thẳng y = 2. Tính thể tích khối tròn xoay tạo được khi quay B quanh trục tung.
Lời giải:
a) Thể tích cần tìm là:
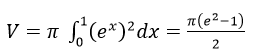
b) Thể tích cần tìm là:
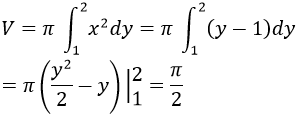
Bài 17 (trang 213 sgk Giải Tích 12 nâng cao):
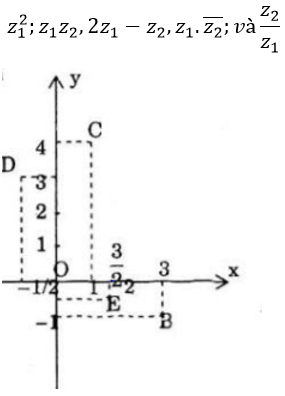
Cho các số phức z1=1+i;z2=1-2i. Hãy tính và biểu diễn hình học các số phức: z12;z1 z2,2z1-z2,z1.Z2−;và z2/z1 .
Lời giải:
Ta có: z12=(1+i)2=1+2i+i2=1+2i-1=2i
z1 z2=(1+i)(1-2i)=1+2+i-2i=3-i
2z1-z2=2(1+i)-(1-2i)=1+4i
z1.¯(z2 )=(1+i)(1+2i)=-1+3i
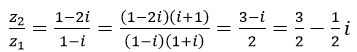
Các điểm A, B, C, D, D lần lượt biểu diễn các số:
Bài 18 (trang 214 sgk Giải Tích 12 nâng cao):
Tính
a) (√3+i)2-(√3-i)2
b) (√3+i)2+(√3-i)2
c) (√3+i)3-(√3-i)3
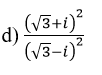
Lời giải:
a) (√3+i)2-(√3-i)2=(3+2 √3 i-1)-(3-2 √3 i-1)=4 √3 i
b) (√3+i)2+(√3-i)2=(3+2 √3 i-1)+(3-2 √3 i-1)=4
c) (√3+i)3-(√3-i)3=(3 √3+9i-3 √3-i)-(3 √3-9i-3 √3+i)=16i
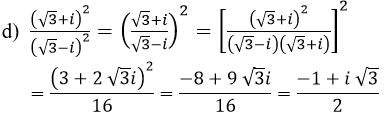
Bài 19 (trang 214 sgk Giải Tích 12 nâng cao):
a) Xác định phần thực của số phức
b) Chứng minh rằng nếu
![]()
Lời giải:
a) Giả sử z=a+bi với a2+b2=1 và a+bi ≠ 1
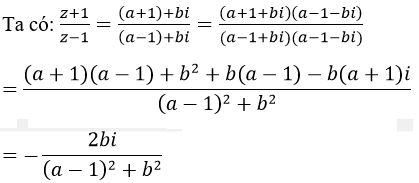
(vì a2+b2=1=>(a+1)(a-1)+b2=0)
Vậy số phức (z+1)/(z-1) có phần thực bằng 0.
b) Theo câu a, ta có:
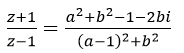
Nên (z+1)/(z-1) là số ảo thì a2+b2-1=0 <=> a2+b2=1 <=> |z| = 1 (đpcm)
Bài 20 (trang 214 sgk Giải Tích 12 nâng cao): Xác định tập hợp các điểm M trên mặt phẳng phức biểu diễn các số phức (+i√3)z+2, trong đó |z-1|≤2
Lời giải:
Giả sử z=x+yi,vì |z-1|≤2 nên (x-1)2+y4≤4 (1)
Ta có:
w=(1+√3 i)z+2=(1+√3 i)(x+yi)+2=(x-√3 y+2)+i(x√3+y)
Gọi N là điểm biểu diễn số phức w => N(x-√3 y+2;x√3+y)
Từ (1) ta có: 4[(x-1)2+y2 ]≤16 <=> (x-1)2+3y2]+[3(x-1)2+y2 ]≤16
<=> (x-1-√3 y)2+(√3 (x-1)+y)2≤16 <=> (xN-3)2+(yN-√3)2≤16
Vậy tập hợp các điểm N nằm trong hình tròn có tâm A(3;√3) có bán kính R = 4.
Bài 21 (trang 214 sgk Giải Tích 12 nâng cao):
Tìm căn bậc hai của mỗi số phức: -8+6i;3+4i;1-2√2 i
Lời giải:
Gọi a+bi là căn bậc hai của -8+6i, ta có:
(a+bi)2=-8+6i <=>(a2-b2 )+2abi=-8+6i
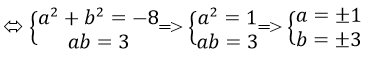
Vậy số -8+6i căn bậc hai là: 1 +3i; 1 – 3i.
Tương tự, số 3 + 4i có căn bậc hai là: 2 +I; 2 -I;
Số 1-2 √2 i có căn bậc hai là: √2-i và – √2+i
Bài 22 (trang 214 sgk Giải Tích 12 nâng cao):
a) Giải phương trình: z2-3+3=0
b) Giải phương trình: z2-(cosα+i sinα )z+i sinα cosα=0
Lời giải:
a) Ta có biệ số Δ=-3+4i=(2i-1)2 nên Phương trình có hai nghiệm là z1=i+1;z2=2-1
b) Ta có biệt hiệu số Δ=(cosα+i sinα )2-4i sinα cosα=cos(-2 α)+i sin(-2 α)
Δ có hai căn bậc hai là: cos(-α)+i sin(-α) và (-cos(-α)-i sin(-α)
Nên Phương trình có nghiệm là:
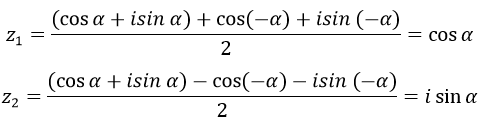
Bài 23 (trang 214 sgk Giải Tích 12 nâng cao):
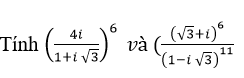
Lời giải:
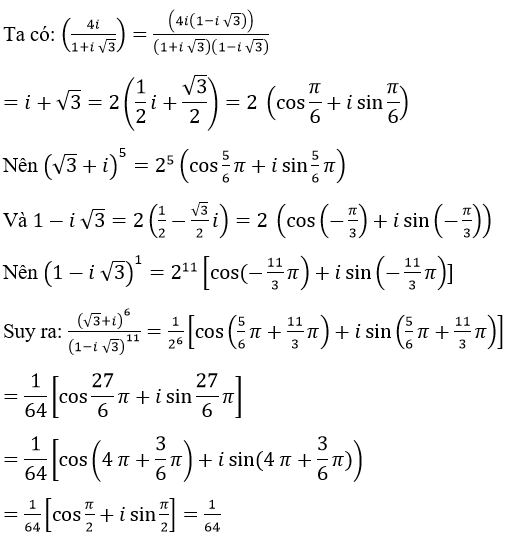
Bài 24 (trang 214 sgk Giải Tích 12 nâng cao):
![]()
A. Đồng biến trên mỗi khoảng (-∞;1)và (3; +∞)
B. Nghịch biến trên mỗi khoảng (-∞;1) và (3; +∞)
C. Đồng biến trên khoảng (-∞;1) và nghịch biến trên khoảng (3; +∞)
D. Nghịch biến trên khoảng (-∞;1) và đồng biến trên khoảng (3; +∞)
Lời giải:
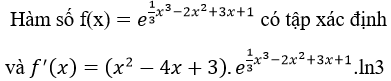
Dấu của f’(x) là dấu của tam thức x2-4x+3
Ta có bảng xét dấu f’(x):

Vậy f(x) đồng biến trên (-∞;1] và [3; +∞)
Ta chọn A.