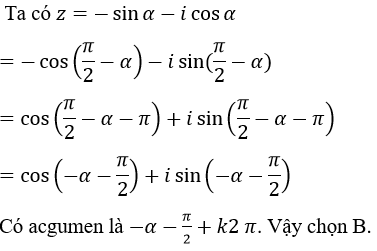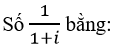
Bài 43 (trang 210 sgk Giải Tích 12 nâng cao):
Phần thực của z = 2i là:
A. 2 B. 2i C. 0 D. 1
Lời giải:
Số z=2i=0+2i nên có phần thực bằng 0. Vậy chọn C.
Bài 44 (trang 210 sgk Giải Tích 12 nâng cao):
Phần ảo của z = -2i là:
A. -2 B. -2i C. 0 D. -1
Lời giải:
Số z = -I = 0 – 2i nên có phần ảo là -2. Vậy chọn A
Bài 45 (trang 210 sgk Giải Tích 12 nâng cao): Số z+z− là:
A. Số thực B. Số ảo C. 0 D. 2
Lời giải:
Giả sử z=a+bi=>z−=a-bi nên z + z− = 2a. vậy chọn A
Bài 46 (trang 210 sgk Giải Tích 12 nâng cao):
Số z-z− là:
A. Số thực B. Số ảo C. 0 D. 2i
Lời giải:
Giả sử z=a+bi=>z−=a-bi nên z – z− = 2bi. Vậy chọn B
Bài 47 (trang 210 sgk Giải Tích 12 nâng cao):
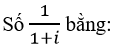
A. 1+i B. (1-i)/2 C. 1-i D. i
Lời giải:
![]()
Vậy chọn B
Bài 48 (trang 210 sgk Giải Tích 12 nâng cao):
Tập hợp các nghiệm của phương trình:
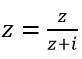
Lời giải:
![]()
<=> z(z+i)=z <=> z(z+i-1)=0
<=> z = 0 và z = 1 – i. vậy chọn A.
Bài 49 (trang 210 sgk Giải Tích 12 nâng cao):
Mô đun của 1 – 2i bằng:
A. 3 B. √5 C. 2 D. 1
Lời giải:
Mô đun của z = 1 – 2i là |z| = √(1+4)=√5. Vậy chọn B.
Bài 50 (trang 210 sgk Giải Tích 12 nâng cao):
Mô đun của -2iz bằng:
A. -2|z| B. √2 z C. 2|z| D. 2
Lời giải:
Mô đun của z’ = -2iz là |z’| = 2.|z|. vậy chọn C.
Bài 51 (trang 210 sgk Giải Tích 12 nâng cao):
Acgumen của -1 + I bằng:
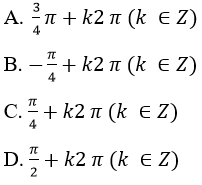
Lời giải:
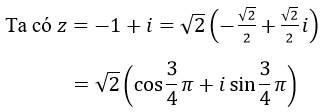
Nên z có acgumen của z là:
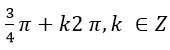
Vậy chọn A.
Bài 52 (trang 211 sgk Giải Tích 12 nâng cao):
Nếu acgumen của z bằng (-π/4) + k2π thì:
A. Phần ảo của z là số dương và phần thực của z bằng 0.
B. Phần ảo của z là số âm và phần thực của z bằng 0.
C. Phần thực của z là số âm và phần ảo của z bằng 0.
D. Phần thực và phần thực của z đều là số âm.
Lời giải:
Nếu acgumen của z bằng (-π/2)+k2 π thì ta có:
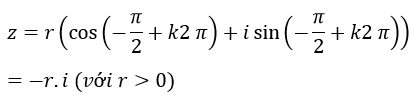
Nên z có phần ảo là -r < 0 và phần thực bằng 0. Vậy chọn B.
Bài 53 (trang 211 sgk Giải Tích 12 nâng cao):
Nếu z=cosα-i sinα thì acgumen của z bằng:
A. α+k2 π B. -α+k2 π
C. α+π+k2 π (k ∈Z) D. pa-α+k2 π (k ∈Z)
Lời giải:
Ta có: z=cosα-i sinα=cos(-α)+i sin(-α) nên z có acgumen là: -α+k2 π. Vậy chọn B.
Bài 54 (trang 211 sgk Giải Tích 12 nâng cao):
Nếu z=-sinα-i cosα thì acgumen của z bằng:
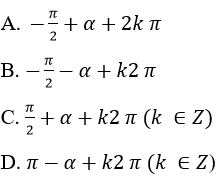
Lời giải: