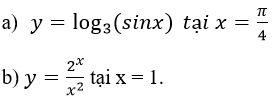
Bài 59 (trang 117 sgk Giải Tích 12 nâng cao):
Tính giá trị gần đúng của đạo hàm của mỗi hàm số sau tại điểm đã cho (chính xác đến hàng phần trăm)
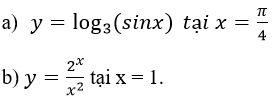
Lời giải:
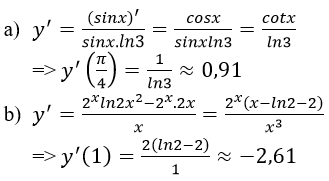
Bài 60 (trang 117 sgk Giải Tích 12 nâng cao):
a) Chứng minh rằng đồ thị hàm số y=ax và y=(1/a)x đối xứng với nhau qua trục tung.
b) Chứng minh rằng đồ thị của hai hàm số y=logax và y=log1/ax đối xứng nhau qua trục hoành.
Lời giải:
a) Gọi (C1) và (C2) lần lượt là đồ thị của các hàm số
![]()
M(x0,y0 ) là một điểm bất kì. Khi đó điểm đối xứng với M qua trục tung là M'(-x0;y0)
Ta có: M ∈(C1 ) <=> y0=ax0
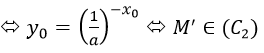
Điều đó chứng tỏ (C1) và (C2 )đối xứng nhau qua trục tung.
b) Chứng minh tương đương bài a, chú ý điểm đối xứng với M(x0;y0 ) qua trục hoành là điểm M'(x0; -y0)
M ∈(C1 )<=> y0=logax0 <=> y0=-log1/ax0 <=> -y0=log1/ax0 <=> M’∈(C2)
Bài 61 (trang 118 sgk Giải Tích 12 nâng cao):
Vẽ đồ thị hàm số y=log0,5x. dựa vào đồ thị hãy giải các bất Phương trình sau:
a) log0,5x > 0 b) -3 ≤ log0,5x < -1
Lời giải:
Đồ thị hàm số là hình vẽ bên.
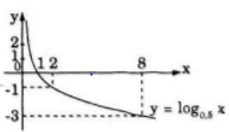
a) log0,5x > 0 là những điểm nằm ở phía trên trục hoành.
log0,5x > 0 <=> 0 < x < 1
b) -3 ≤ log0,5x < -1 ( y=log0,5x là những điểm trên đồ thị có tung độ thuộc nửa khoảng [-3; 1))
-3 ≤ log0,5x < -1 <=> 2 < x≤8
Bài 62 (trang 118 sgk Giải Tích 12 nâng cao):
Vẽ đồ thị hàm số y=(√3)x. dựa vào đồ thị, hãy giải các bất Phương trình sau:
a) (√3)x ≤ 1 b) (√3)x < 3
Lời giải:
Đồ thị hàm số y=(√3)x có hình vẽ bên.
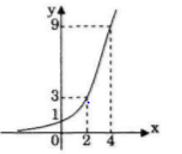
a) (√3)x < 1 (tung độ y=(√3)x không lớn hơn 1)
=> (√3)x ≤ 1 <=> x ≤ 0
b) (√3)x > 3 (tung độ y=(√3)x lớn hơn 3)
=> (√3)x > 3 <=> x > 2