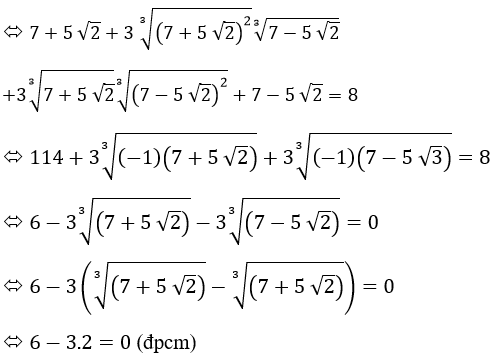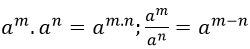
Bài 1 (trang 75 sgk Giải Tích 12 nâng cao):
Trong các khẳng định sau, khẳng định nào đúng khẳng định nào sai?
a) Với số thực a và số nguyên m, n, ta có:
![]()
b) Với số thực a, b cùng khác 0 và số nguyên n, ta có:
![]()
c) Với số thực a, b thỏa mãn 0 < a < b với số nguyên a, ta có am < bn
d) Với số thực a ≠ 0 và hai số nguyên m, n. ta có: Nếu m > n thì am > an
Lời giải:
a) Sai:
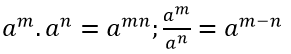
b) Đúng
c) Sai. Chẳng hạn: a0=b0
d) Sai. Chẳng hạn (−1)3 < (−1)2
Bài 2 (trang 75 sgk Giải Tích 12 nâng cao):
Xét khẳng định: “Với số thực a và hai số hữu tỉ r, s, ta có (ar )s=ars. Với điều kiện nào trong các điều kiện sau thì khẳng định trên là đúng:
A. A bất kì B. a ≠ 0 C. a > 0 D. a < 0
Lời giải:
Bài 3 (trang 76 sgk Giải Tích 12 nâng cao):
Viết các dạng số sau dưới dạng số nguyên hay phân phố tối giải:
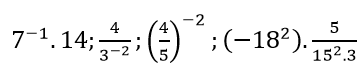
Lời giải:
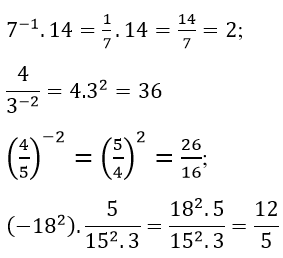
Bài 4 (trang 76 sgk Giải Tích 12 nâng cao):
Thực hiện phép tính:
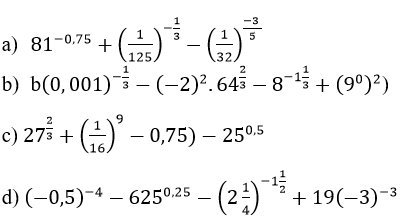
Lời giải:
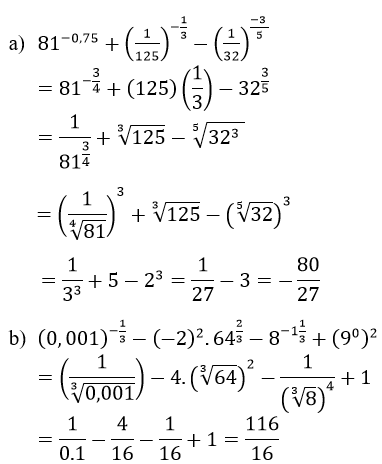
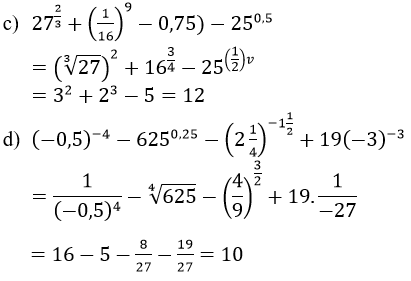
Bài 5 (trang 76 sgk Giải Tích 12 nâng cao):
Đơn giản biểu thức
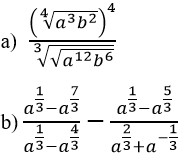
Lời giải:
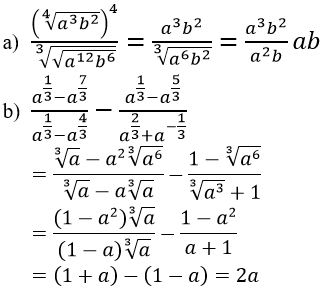
Bài 6 (trang 76 sgk Giải Tích 12 nâng cao):
So sánh các số:
a) √2 và ∛3
b) √3+∛30 và ∛63
c) ∛7+√15 và √10-∛28
Lời giải:
a) Giả sử √2 < ∛3 <=> (√2)2 < 3 <=> 2 √2 < 3 <=> 8 < 9 đúng.
Vậy √2 < ∛3
b) Giả sử √3+∛30 < ∛63 <=> 3 √3+9 ∛30+3 √3∛(302 )< 63-30
<=> 3 √3+9∛3- +3 √3 ∛(302 ) < 33 (*)
Ta có 3∛3 > 3
9∛30 > 9∛27=27
3 √3 ∛(302 ) > 3 ∛27.27=27 => ∛3+9∛30+3 √3 ∛(302 ) > 57 > 33
Vậy (*) sai => √3+∛30 > ∛63
c) Giả sử ∛7+√15 > √10-∛28<=> √15-√10 > ∛28-∛7
<=> 5-2 √150 > ∛28-2∛28.7+∛(72 )
<=> 5+2∛28.7 > ∛(282 )+2 √155+∛(72 )
Do 2 √155 > 2 √125=2.5=10 > 5
∛(282 )+2 √155+∛(72 )=2+2∛(28.72.2) > 2∛28.7
Vậy 5+2∛28.7 < ∛(282 )+2 √155+∛(72 ) => (*) sai. Vậy ∛7+√15 < √10-∛28
Bài 7 (trang 76 sgk Giải Tích 12 nâng cao):
Chứng minh
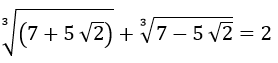
Lời giải:
Ta có: