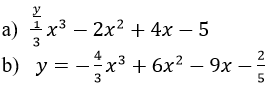
Bài 6 (trang 8 sgk Giải Tích 12 nâng cao):
Xét chiều biến thiên của hàm số sau:
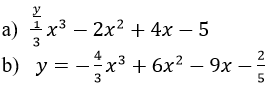
Lời giải:
Hàm số đã cho xác định trên R.
y’=x2-4x+4=(x-2)2>0,∀x ≠ 2;y’=0 chỉ tại x = 2
Vậy hàm số đồng biến trên R.
Hàm số đã cho xác định trên R.
y’=-4x2+12x-9=-(2x-3)2≤0,∀x ∈R;y’=0 chỉ tại x=3/2
Vậy hàm số nghịch biến trên R.
Hàm số đã cho xác định trên D = R \ {5}
![]()
Nên hàm số đồng biến trên khoảng (-∞;5)và (5; +∞)
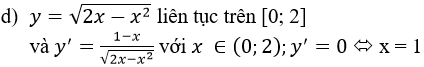
Chiều biến thiên của hàm số được nên trong bảng sau:
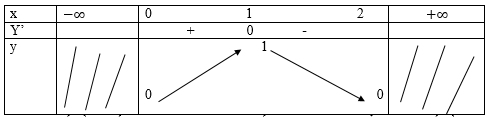
Vậy hàm số đồng biến trên [0; 1] và nghịch biến trên [1; 2] (có thể nói hàm số đồng biến trên (0; 1) nghịch biến trên (1; 2))
![]()
(x2-2x+3=(x-1)2+2>0 ∀x ∈R)
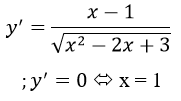
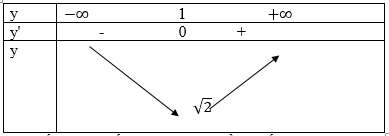
Hàm số nghịch biến trên (-∞;1), đồng biến trên (1; +∞)
Hàm số xác định trên D = R \ {-1}
![]()
∀x ∈D nên hám số nghịch biến trên mỗi khoảng (-∞; -1)và (-1; +∞)
Bài 7 (trang 8 sgk Giải Tích 12 nâng cao):
Chứng minh rằng hàm số f(x) cos2x-2x+3 nghịch biến trên R.
Lời giải:
f(x) xác định và liên tục trên R nên liên tục trên mỗi đoạn
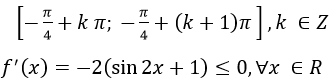
f’(x) = 0 <=> sin 2x = -1 <=> 2x = -π/2+k2 π <=> x=-π/4+k π,k ∈Z
Vậy hàm số nghịch biến trên mỗi đoạn
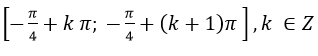
Do đó hám số nghịch biến trên R.
Bài 8 (trang 8 sgk Giải Tích 12 nâng cao):
Chứng minh bất đẳng thức sau:
sinx<x với mọi x > 0; sin x > x với mọi x < 0.
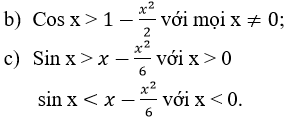
Lời giải:
+ Hàm số f(x) = x-sinx liên tục trên nửa khoảng
[0;π/2) và có đạo hàm f’(x) = 1-cosx>0 ∀x ∈(0;π/2)
Do đó hàm số đồng biến trên [0;π/2). Suy ra: f’(x) > f(0) ∀x ∈(0;π/2) hay x-sinx>0,∀x ∈(0;π/2)
Hiển nhiên x >sin x, ∀x≥π/2 (do sin x ≤1)
Vậy x
sinx với mọi x >0
+ Hàm số f(x) = x – sin x liên tục trên [-π/2;0] và có đạo hàm f’(x) = a- cos x > 0 ∀x ∈(-π/2;0). Do đó hàm số đồng biến trên (-π/2;0)
Hiển nhiên: x < sin x với mọi x≤-π/2 (vì sinx≥-1)
Vậy x < sin x với mọi x < 0
Cách 1. Hàm số g(x) = cos x – 1 + x2/2. Xác định trên R và có đạo hàm g’(x) = x – sin x
Chiều biến thiên của g(x) được thể hiện bảng sau:

Vậy g(x) > 0, ∀x ≠ 0
Cách 2. Xét g(x) = cosx-1+x2/2 liên tục trên nửa khoảng [0; +∞] và có đạo hàm g’(x) = x – sin x. theo a, g’(x) >0 với mọi x> 0
Do đó hàm số g đồng biến trên [0; +∞)
Và ta có: g(x) > g(0), ∀x>0
Tức là cos x – 1 + x2/2>0 với mọi x > 0 (1)
Từ đó suy ra với mọi x < 0, ta có:
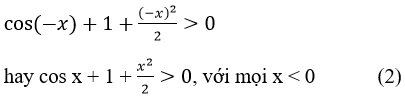
Từ (1) và (2), ta có g(x) > 0 ∀x ≠ 0 hay cos x > 1-x2/2,∀x ≠ 0
Xét h(x) = sin x – x + x2/6 xác định trên R và có đạo hàm h’(x) = cos x – 1 + x/2>0,∀x ≠ 0; h’() = 0 (theo b)
H(x) đồng biến trên R và ta có:
H(x) >h(0) với mọi x > 0 và sinh sinx<x-x2/6 với mọi x < 0
Bài 9 (trang 9 sgk Giải Tích 12 nâng cao):
Chứng minh rằng: sinx+tanx>2x với mọi x ∈(0;π/2)
Lời giải:
Đặt f(x) = sin x + tan x – 2x
Ta có: f(x) liên tục trên [0;π/2) và f’(x) = cosx+1/cos2x -2
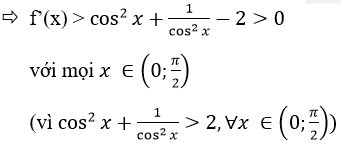
do hàm số f đồng biến trên [0;π/2) và ta có (x) > f(0) ∀x ∈(0;π/2)
hay sin x + tan x > 2x với mọi x ∈(0;π/2)
Bài 10 (trang 9 sgk Giải Tích 12 nâng cao):
Số dân của một thị trấn t năm kể từ năm 1970 ước tính bởi công thức
![]()
(f(t) được tính bằng nghìn người)
tính số dân của thị trấn vào đầu năm 1908 và đầu năm 1995
Xem f là một hàm số xác định trên nửa khoảng [0; +∞). Tính f’(t) và xét chiều biến thiến của h trên nửa khoảng [0; +∞)
Đạo hàm của hàm số f biểu thị tốc độ tăng dần của thị trấn (tính bằng nghìn người/năm)
Tính tốc độ tăng dân số vào năm 1990 của thị trấn.
Tính tốc độ tăng dân số được dự kiến vào năm đầu 2008.
Vào năm nào thì tốc độ tăng dần số là 0,125 nghìn /người.
Lời giải:
a) Vào đầu năm 1908, ta có t = 10; f’(10)= 18
Vậy số dân của thị trấn vào đầu năm 1980 là 18 nghìn người.
Vào đầu năm 1995, ta có t = 25, f(25) = 22
Số dân của thị trấn vào đầu năm 1995 là 22 nghìn người.
![]()
f(t) liên tục trên [0; +∞) (vì liên tục trên khoảng (-5; +∞))
vậy hàm số đồng biến trên [0; +∞)
tốc độ tăng dân số vào đầu năm 1990 là:
f’(2) = 120/252 =0,192 (do t = 1990 – 1970 = 20 )
tốc độ tăng dân số được dự kiến vào năm 2008 của thị trấn là:
f’(38)=120/432 ≈0,065 (do t = 2008 – 1970) = 38)
Ta có f’(t) = 0, 125
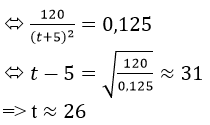
Vậy năm 1996. Tốc độ tăng dân số của thị trấn là 0, 125.
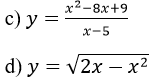
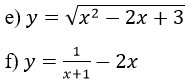
[…] (2; toan123.vn Bài 1: SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ Toan123.vn lop12.edu.vn Đại số – Chương 1 – Luyện tập (trang 8-9) Bài 6 (trang 8 sgk Giải Tích 12 nâng […]
Comments are closed.