Đại số – Chương 1 – Luyện tập (trang 50)

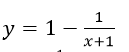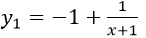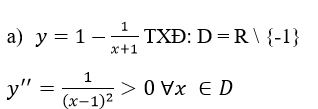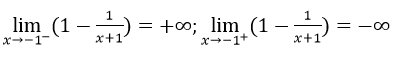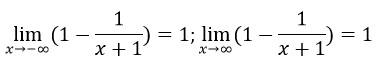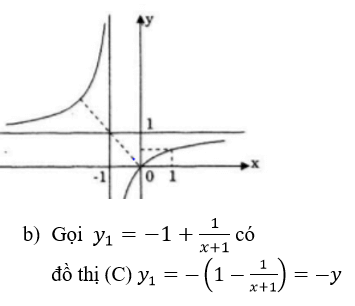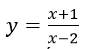
Bài 53 (trang 50 sgk Giải Tích 12 nâng cao):

a) Khảo sát sự biến thiên của đồ thị hàm số

b) Viết Phương trình tiếp tuyến của đồ thị hàm số đã cho tại giao điểm của A với trục tung.

c) Viết Phương trình tiếp tuyến của đồ thị song song với tiếp tuyến tại điểm A.

Lời giải:

a) TXĐ: D = R \ {2}

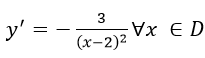
Vậy hàm số đã cho luôn nghịch biến trên (-∞,2) và (2; +∞)

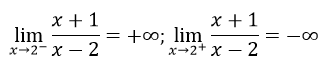
Vậy x = 2 là tiệm cận ngang.

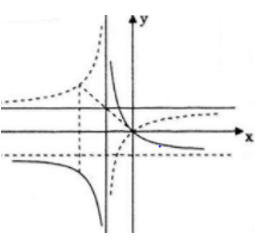
Bảng biến thiên.

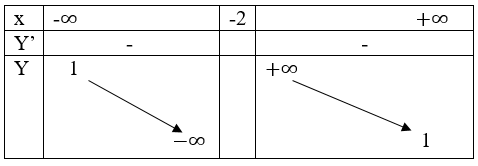
Đặc biệt A(0; 1/2);B(-1;0)

b) A là giao điểm của trục tung nên A(0; 1/2) Phương trình tiếp tuyến tại A có dạng

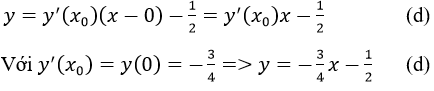
c) Gọi Δ là Phương trình tiếp tuyến song song với d nên Δ có hệ số

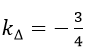
=> Phương trình tiếp tuyến Δ có dạng

Vì Δ là tiếp tuyến của (C) nên ta có:

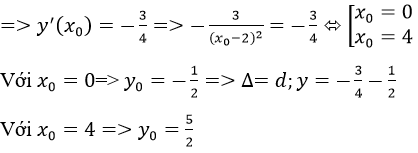
Phương trình đường thẳng Δ là:

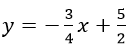
Bài 54 (trang 50 sgk Giải Tích 12 nâng cao):

a) Khảo sát sự biến thiên và vẽ đồ thị H của hàm số

b) Từ đồ thị hàm số (H) suy ra cách vẽ đồ thị

Lời giải:

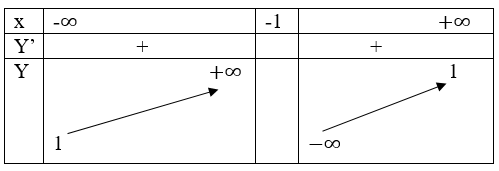
Hàm số luôn đồng biến trên khoảng (-∞; -1) và (-1; +∞)

Vậy đường thẳng x = -1 là tiệm cận đứng.

Vậy đường thẳng y = 1 là tiệm cận ngang.

Bảng biến thiên

Đặc biệt A(0; 0); B(1; 1/2)

=> Cách vẽ đồ thị (C): đồ thị hàm số đối xứng với (H) qua trục hoành.

Bài 55 (trang 50 sgk Giải Tích 12 nâng cao):

a) Khảo sát sự biến thiên của đồ thị hàm số

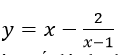
b) Viết phương trình tiếp tuyến của đồ thị hàm số dá cho biết rằng tiếp tuyến đó đi qua điểm A(3; 3)

Lời giải:

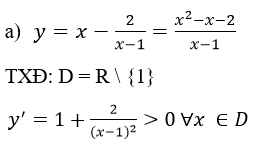
Vậy hàm số luôn đồng biến trên (-∞;1)và (1; +∞)

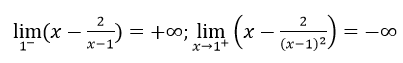
Vậy đường thẳng x = 1 là tiệm cận đứng.

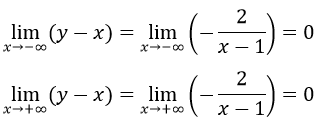
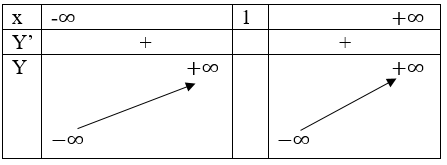
Bảng biến thiên

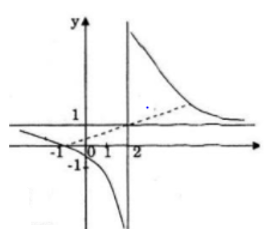
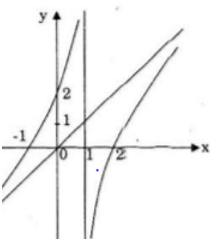
Đồ thị

Giao với Ox: (-1; 0); (2; 0)

Giao với Oy: (0; 2)

b) Gọi Phương trình đường thẳng (d) có hệ số góc k đi qua A(3; 3) có dạng y-3=k(x-3) <=> y=k(x-3)+3

(d) là tiếp tuyến của đồ thị hàm số khi và chỉ khi hệ Phương trình sau có nghiệm”

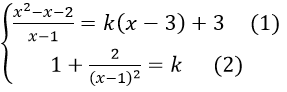
Thế (2) vào (1) ta được

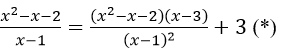
(*) => (x²-x-2)(x-1)=(x²-2x+3)(x-3)+3(x-1)²

<=> 4x=8 => x = 2

Với x = 2 => k = 3. Vậy phương trình tiếp tuyến là

y=3(x-3)+3 <=> y=3x+6

Bài 56 (trang 50 sgk Giải Tích 12 nâng cao):

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số

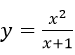
b) Từ đồ thị hàm số đã cho suy ra cách vẽ đồ thị của hàm số

Lời giải:

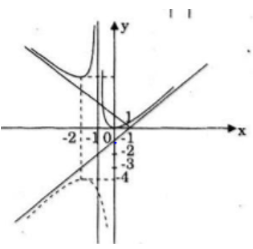
a) TXĐ: D = R \ {-1}

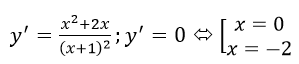
Hàm số đồng biến trên khoảng (-∞; -2) và (0; +∞)

Hàm số nghịch biến trên (-2; -1) và (-1; 0)

y_CĐ=y(-2)=-4;y_CT=y(0)=0

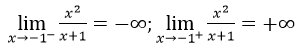
Vậy đường thẳng x = -1 là tiệm cận đứng.

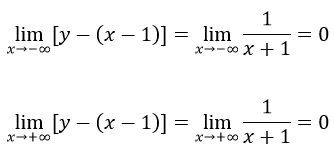
Vậy đường thẳng y = x – 1 là tiệm cận xiên

Bảng biến thiên.

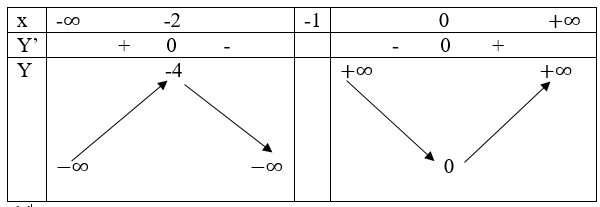
Đồ thị

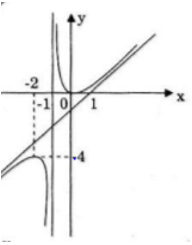
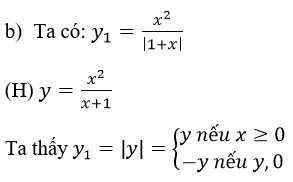Do đó (H) được suy ra từ (C) như sau: (H) và (C) trùng nhau khi (C) ở phía trên trục hoành. (H) và (C) đối xứng nhau qua trục hoành khi (C) ở phía dưới trục hoành.

Comments

comments