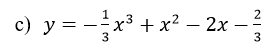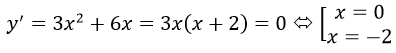
Bài 40 (trang 43 sgk Giải Tích 12 12 nâng cao):

a) Khảo sát và vẽ đồ thị hàm số y=x³+3x²-4

b) Viết phương trình tiếp tuyến của đồ thị tại điểm uốn.

c) Chứng minh rằng điểm uốn làm tâm đối xứng của đồ thị.

Lời giải:

a) TXĐ: R

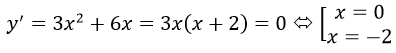
y’>0 trên khoảng (-∞; -2)và (0; +∞)

y'<0 trên khoảng (-2; 0)

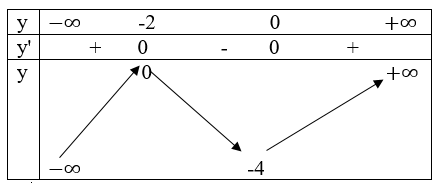
y_CĐ=y(-2)=0; y_CT=y(0)=-4

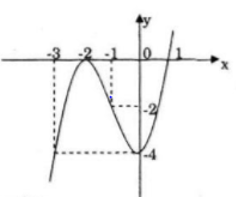
y”=6x+6=6(x+1)=0 <=> x = -1

Bảng xét dấu y’’

X	-∞		-1		+∞
Y’’		–	0	+
Đồ thị		Lồi	điểm uốn u(-1; -2)	lõm

Hàm số lồi trên khoảng (-∞; -1)

Hàm số lõm trên khoảng -1; +∞)

Hàm số có 1 điểm uốn u(-1; -2)

Bảng biến thiên:

Đồ thị

Đi qua điểm (1; 0) và (-3; -4)

b) Hàm số y=x³+3x²-4 có điểm uốn u(-1; -2)

Ta có: y’=3x²-4 ; y’(-1) = -3

Phương trình tiếp tuyến tại điểm uốn u(-1; -2) có dạng

y-y₀=y'(x₀)(x-x₀)

<=> y+2=-3(x+1)

<=> y=-3x-5

Vậy phương trình tiếp tuyến tại điểm uốn là: y = -3x – 5.

c) Đồ thị nhận I(-1; -2) là tâm đối xứng khi và chỉ khi:

f(x₀+x)+f(x₀-x)=2y₀ với ∀x

<=> f(x-1)+f(-x-1)=-4 ∀x

<=> (x-1)³+3(x-1)²-4+(-1-x)³+3(-1-x)²-4 ∀x

<=> x³-3x²+3x-1+3x²-6x+3-5-3x-3x²-x³+3+6x+3x²-4=-4 ∀x

<=>-4=4 ∀x

=> I(-1; -2) là tâm đối xứng của đồ thị.

Bài 41 (trang 44 sgk Giải Tích 12 12 nâng cao):

a) Khảo sát và vẽ đồ thị của hàm số y=-x³+3x²-1

b) Tùy theo các giá trị của m hãy biện luận số nghiệm của phương trình -x³+3x²-1=m

Lời giải:

a) y=-x³+3x²-1. Tập xác định D = R

y’=-3x^2+6x

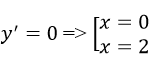
– Hàm số đồng biến trên khoảng (0;2)

– Hàm số nghịch biến trên khoảng (-∞;0)và (2; +∞)

y_CĐ=y(2)=3; y_CT=y(0)=-1

y”=-6x+6;y”=0 => x = 1

– Hàm số lồi trên khoảng (-∞;1) lõm trên khoảng (1;+∞)

– Hàm số có một điểm uốn I(1; 1)

Bảng biến thiên:

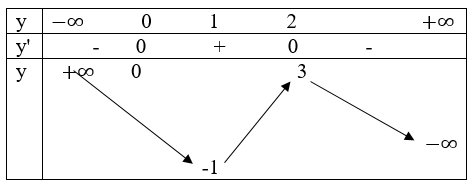
Đồ thị đi qua (0; -1)

Bài 42 (trang 44 sgk Giải Tích 12 12 nâng cao): 

Khảo sát và vẽ đồ thị của các hàm số sau:

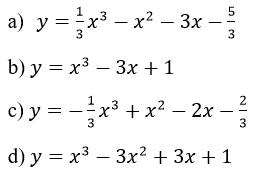
Lời giải:

a) * TXĐ: R

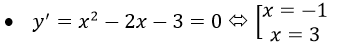
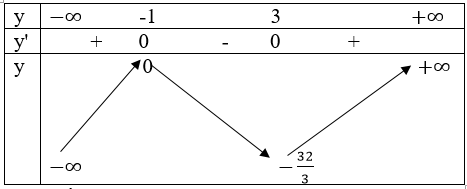
y’> 0 trên khoảng (-∞; -1)và(3; +∞)

y'< 0 trên khoảng (-1; 3)

y_CT=y(3)=-32/3;y_CĐ=y(-1)=0

y”=2x-2=2(x-1)=0 <=> x = 1

Bảng xét dấu y’’

Hàm số lồi trên khoảng (-∞; -1).

Hàm số lõm trên khoảng (1; +∞)

Hàm số có 1 điểm uốn u(1; -16/3)

Bảng biến thiên

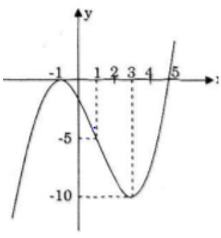
– Đồ thị

Đi qua (0; -5/3);(5;0)

b) TXĐ: R

y’=3x^2-3=0 <=> x=±1

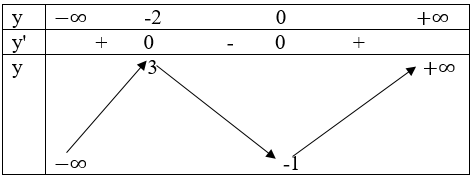
y’> 0 trên khoảng (-∞; -1)và (1; +∞)

y'< 0 trên khoảng (-1; 1)

y_CĐ=y(-1)=3;y_CT=y(1)=-1

Bảng xét dấu y’’

X	-∞		0		+∞
Y’’		–	0	+
Đồ thị	Lồi		điểm uốn u(0; 1)	lõm

Hàm số có 1 điểm uốn u(0; 1)

• Bảng biến thiên

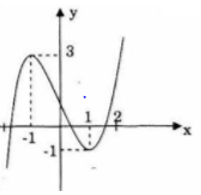
• Đồ thị

Đi qua (0; 1)

+ Tập xác định D = R.

y’=-x²+2x-2=-[(x-1)²+1]<0 ∀x ∈D

– Hàm số luôn nghịch biến trên khoảng (-∞; +∞)

– Hàm số không có cực trị

– Đồ thị không có tiệm cận.

y”=-2x+2;y”=0 => x = 1

– Hàm số lồi trên (1; +∞)lõm trên (-∞;1) nhận I(1; -2) làm điểm uốn.

Bảng biến thiên.

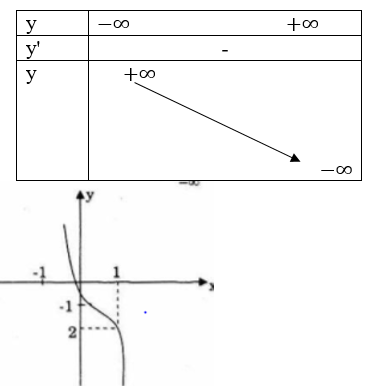
d) y=x³-3x²+3x+1

Tập xác định D = R

y’=3x²-6x+3=3(x-1)²>0 ∀x ∈D

– Hàm số luôn đồng biến (-∞; +∞)

– Hàm số không có cực trị

– Đồ thị không có tiệm cận

y”=6x-6;y”=0 => x = 1

– Đồ thị lồi trên (-∞;1)

– Đồ thị lõm trên (1; +∞)

Đồ thị nhận I(1; 2) làm tâm đối xứng.

Bảng biến thiên

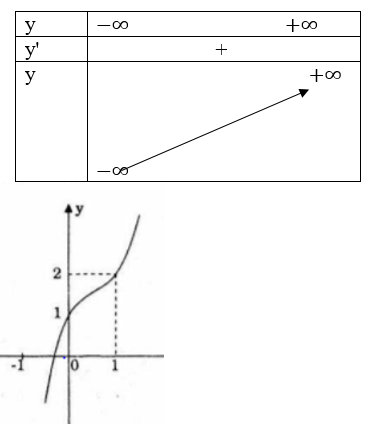
Bài 43 (trang 44 sgk Giải Tích 12 12 nâng cao):

a) Khảo sát và vẽ đồ thị hàm số sau: y=-x⁴+2x²-2

b) Tùy theo các giá trị của m hãy biện luận số nghiệm của phương trình -x⁴+2x²-2=m

c) Viết Phương trình tiếp tuyến tại các điểm uốn của đồ thị.

Lời giải:

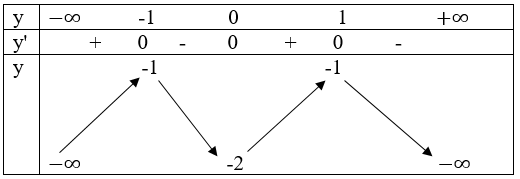
a) TXĐ: R

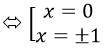
* y’=-4x³+4x=4x(-x²+1)=0

y’>0 trên khoảng (-∞; -1)và (0;1)

y'<0 trên khoảng (-1;0) và (1; +∞)

y_CT=y(0)=-2;y_CĐ=y(-1)=-1

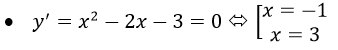
– y”=-12x²+4=4(-3x²+1)=0

Bảng xét dấu y’’

Bảng biến thiên.

• Đồ thị

Đồ thị nhận Oy làm trục đối xứng giao với Oy (0; -2)

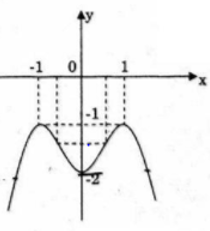
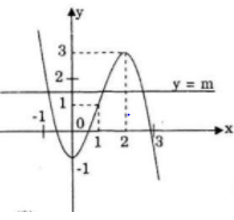
b) Số nghiệm của Phương trình -x⁴+2x²-2=m (1) là giao điểm của đồ thị y=-x⁴+2x²-2 với đường thẳng y = m.

Nếu m > -1 thì Phương trình (1) vô nghiệm.

Nếu m = 1 thì Phương trình (1) có 2 nghiệm.

Nếu -2 < m < -1: Phương trình có 4 nghiệm.

Nếu m = -2 phương trình (1) có 3 nghiệm

Nếu m < -2: Phương trình (1) có 2 nghiệm

Kết luận:

m > -1: Phương trình (1) vô nghiệm.

Phương trình (1) có 2 nghiệm.

m=−2: Phương trình (1) có 3 nghiệm.

-2 < m < -1 phương trình (1) có 4 nghiệm.

c) Hàm số y=-x⁴+2x²-2 có 2 điểm uốn đó là:

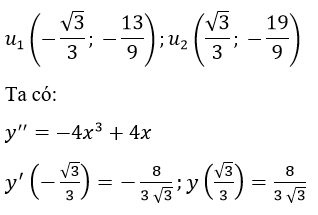
Phương trình tiếp tuyến uốn

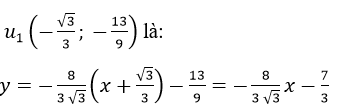
Phương trình tiếp tuyến tại điểm uốn

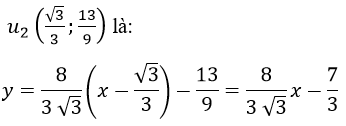
Vậy đồ thị hàm số đã cho có 2 tiếp tuyến:

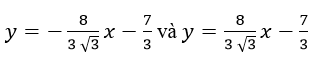
Bài 44 (trang 44 sgk Giải Tích 12 12 nâng cao): 

Khảo sát và vẽ đồ thị hàm số sau:

a) y=x⁴-3x²+2     b) y=-x⁴-2x²+1

Lời giải:

a) TXĐ: R

y’=4x³-6x=2x(2x²-3)=0

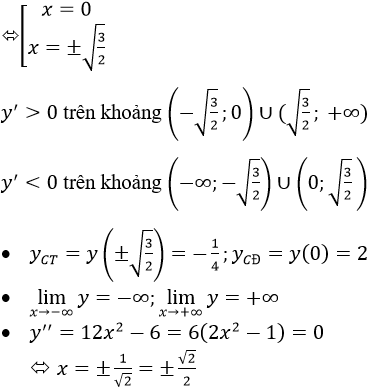
•Bảng xét dấu y’’

• Bảng thiên thiên

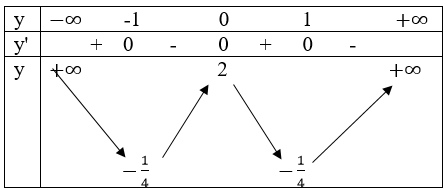
• Đồ thị

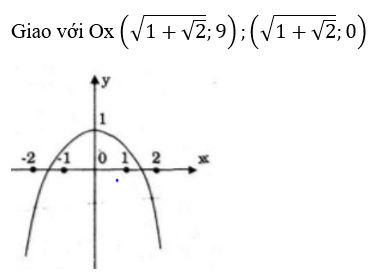
Đồ thị nhận Oy làm trục đối xứng

Giao với Oy (0; 2)

Giao với Ox (-1; 0); (1; 0)

(-√2;0);(√2;0)

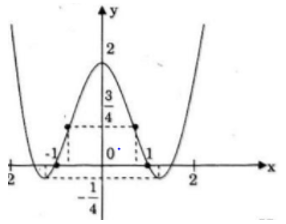
b) y=-x⁴-2x²+1

TXĐ: R

y’=-4x⁵-4x=4x(x²-1)=0 <=> x=0

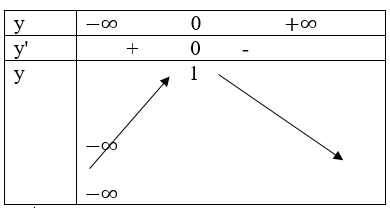
y’> 0 trên khoảng (-∞;0),y'< 0 trên khoảng (0; +∞)

y_CĐ=y(0)=1

y”=-12x²-4<0 ∀x ∈R

Bảng xét dấu y’’

X	-∞	–	+∞
Y’’		Lồi
Đồ thị

Hàm số lồi trên khoảng (-∞; +∞)

Bảng biến thiên

Đồ thị

Đồ thị nhận Oy làm trục đối xứng giao với Oy (0; 1)

Comments

comments