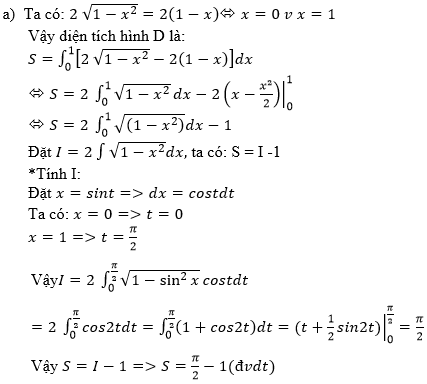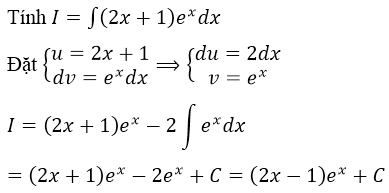
Bài 1 (trang 126 SGK Giải tích 12):
a) Phát biểu định nghĩa nguyên hàm của hàm số f(x) trên một khoảng.
b) Nêu phương pháp tính nguyên hàm từng phần. Cho ví dụ minh họa.
Lời giải:
a) Cho hàm số f(x) xác định trên K ( k là nửa khoảng hay đoạn của trục số). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F‘(x)=f(x) với mọi x thuộc K.
Định lý: Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì:
– Với mỗi hằng số C, F(x) + C cũng là một nguyên hàm của hàm số trên f(x) trên K.
– G(x) cũng là một nguyên hàm của hàm số f(x) trên K thì tồn tại một hằng số C sao cho G(x) = F (x) +C
b)
*Đổi biên số:
Nếu ∫f(u)du=F(u)+C va u(x) là hàm số có đạo hàm liên tục thì:
∫f(ux) u‘(x)dx=F(u(x))+C
*Tính nguyên hàm từng phần:
Nếu hai hàm số u= u(x) và v = v(x) có đạo hàm liên tục trên K thì:
∫u(x) v‘(x)dx=u(x)v(x)- ∫v(x) u‘(x)dx
Hay ∫udv=uv- ∫vdv.
Ví dụ:
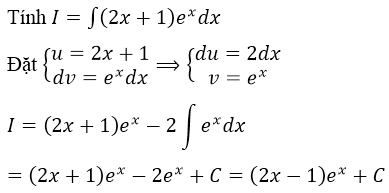
Bài 2 (trang 126 SGK Giải tích 12):
a) Phát biểu định nghĩa tích phân của hàm số f(x) trên một đoạn.
b) Nêu các tính chất của tích phân. Cho ví dụ minh họa.
Lời giải:
a) Cho hàm số y= f(x) liên tục trên [a; b] , F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là ∫abf(x)dx.
Ta có: ∫abf(x)dx=F(x)ab=F(b)-F(a)
Ta gọi ∫ab là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx biểu thức dưới dấu tích phân, f(x) là hàm số dưới dấu tích phân.
b) Các tính chất
1. ∫aaf(x)dx=0
2. ∫abf(x)dx=- ∫baf(x)dx
3. ∫bakf(x)dx=k. ∫baf(x)dx ( k là hằng số)
4. ∫ab[f(x)±g(x)]dx= ∫abf(x)dx± ∫abg(x)dx
5. ∫abf(x)dx= ∫acf(x)dx+ ∫abf(x)dx(a<c<b)
Bài 3 (trang 126 SGK Giải tích 12): Tìm nguyên hàm của các hàm số sau:
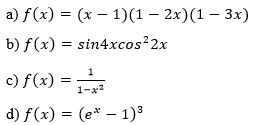
Lời giải

Bài 4 (trang 126 SGK Giải tích 12): Tính:

Lời giải

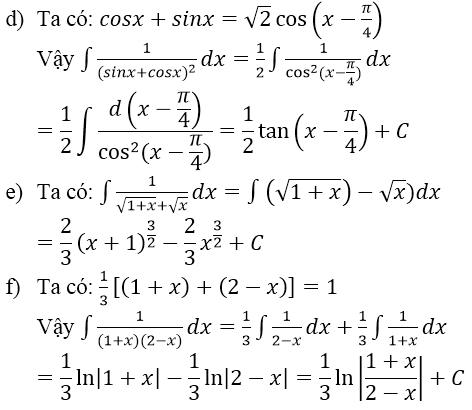
Bài 5 (trang 127 SGK Giải tích 12): Tính:

Lời giải
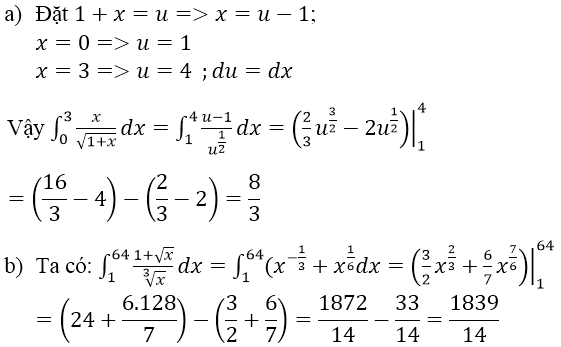
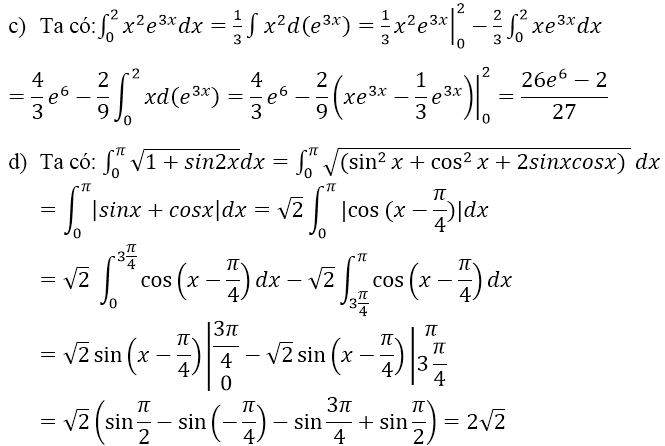
Bài 6 (trang 127 SGK Giải tích 12): Tính:
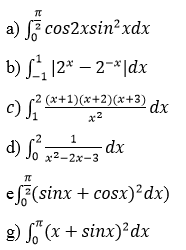
Lời giải
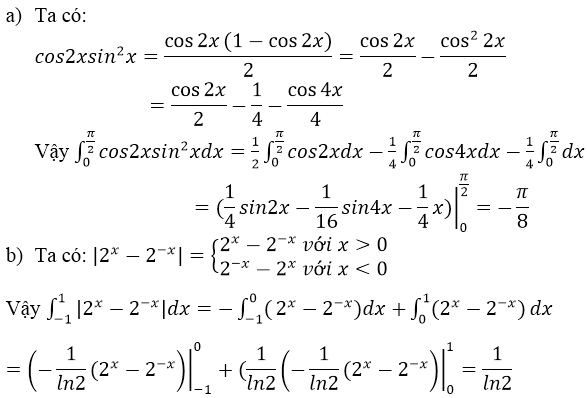
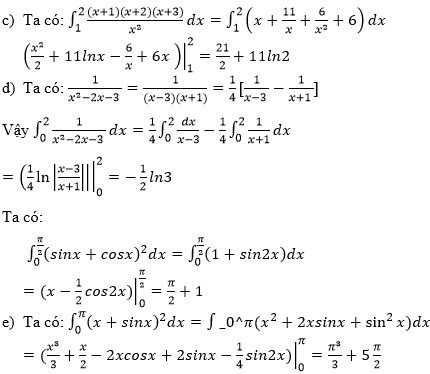
Bài 7 (trang 127 SGK Giải tích 12): Xét hình phẳng D giới hạn bởi y=2√(1-x2 ) và y=2(1-x)
a) Tính diện tích hình D
b) Quay hình D xung quanh trục Ox. Tính thể tích khối tròn xoay được tạo thành.
Lời giải: