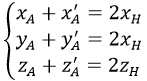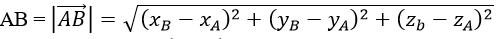
Bài 1 (trang 107 sgk Hình Học 12 nâng cao):
Cho biết tọa độ hai điểm A, B. Làm thế nào để tìm:
a) Tọa độ của vectơ AB→
b) Khoảng cách giữa hai đểm A và B.
c) Tọa độ của trung điểm đoạn AB?
Lời giải:
Cho A(xA,yA,zA) và B(xB,yB,zB)
a) Ta có AB→=(xB-xA );yB-yA ; zB– ZA)
b) Ta có
![]()
c) Tọa độ trung điểm AB là:
![]()
Bài 2 (trang 108 sgk Hình Học 12 nâng cao):
Cho tọa độ bốn đỉnh của một hình tứ diện, làm thế nào để tìm:
a) Tọa độ trọng tâm tứ diện;
b) Tọa độ của tâm và bán kính mặt cầu ngoại tiếp tứ diện;
c) Thế tích tứ diện
d) Độ dài tứ đường cao ứng với một mặt tứ diện?
Lời giải:
Cho tứ diện ABCD có A=(xA,yA,zA), B=(xB;yB,zB); C=(xC,yC,zC), D = (xD,yD,zD)
a) Tọa độ trọng tâm tứ diện là:
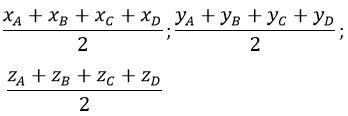
b) Gọi I = (x0;y0;z0) là tâm mặt cầu ngoại tiếp tứ diện ABCD, ta có:
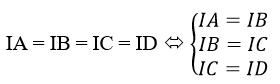
Giải hệ ta tìm được tọa độ (x0;y0;z0) của tâm mặt cầu ngoại tập tứ diện ABCD.
Từ đó, tính được bán kính mặt cầu ngoại tiếp tứ diện ABCD là
![]()
Bài 3 (trang 108 sgk Hình Học 12 nâng cao)
Bằng phương pháp tọa độ, làm thế nào để chứng minh:
a) Hai vectơ cùng phương
b) Ba vectơ đồng phẳng
c) Ba điểm thẳng hàng
d) Bốn điểm không thẳng hàng?
Lời giải:
a) Hai vectơ a→, b→ cùng phương <=> tồn tại số k sao cho a→=k b→ hoặc a→,b→ cùng phương <=> [a→,b→ ]=0→
b) a→,b→,c→ đồng phẳng <= >[a→,b→ ].c→=0→
c) Ba điểm A, B, C thẳng hàng <=> AB→,BC→ cùng phương.
d) Bốn điểm A, B, C không đồng phẳng <=> vectơ AB→,AC→,AD→ không đồng phẳng <=> [AB→.AC→ ].(AD) ⃗ ≠ 0
Bài 4 (trang 108 sgk Hình Học 12 nâng cao):
Trong mỗi trường hợp sau, hãy nêu cách viết phương trình mặt phẳng:
a) Đi qua ba điểm không thẳng hàng
b) Đi qua một điểm và vuông góc với một đường thẳng cho trước.
c) Đi qua một điểm và song song với hai đường thẳng chéo nhau cho trước.
d) Đi qua một đường thẳng và song song với một đường thẳng cho trước.
e) Đi qua một điểm và vuông góc với hai mặt phẳng cho trước.
f) Chứa hai đường thẳng song song hoặc cắt nhau..
g) Đi qua một đường thẳng và vuông góc với một mặt phẳng cho trước.
Lời giải:
a) Mặt phẳng đi qua ba điểm A, B, C không thẳng hàng là mặt phẳng đi qua A và nhận vectơ n→=[AB→.AC→ ] làm vectơ pháp tuyến.
b) Mặt phẳng đi qua A và vuông góc với (d) là mặt phẳng đi qua A và nhận vectơ chỉ Phương của (d) làm vectơ pháp tuyến.
c) Mặt phẳng đi qua A và song song với hai đường thẳng chép nhau d1,d2 là mặt phẳng đi qua A và nhận vectơ n→=[u1→.u2→ ] làm vectơ pháp tuyến, trong đó u1→,u2→ lần lượt là vectơ chỉ Phương của d1 và d2.
d) Mặt phẳng đi qua đường thẳng (d1) và song song với (d2 ) là mặt phẳng đi qua M0∈(d1) và nhận vectơ n→=[u1→,u2→ ] làm vectơ pháp tuyến. trong đó u1→,u2→lần lượt là vectơ chỉ Phương của d1 và d2.
e) Mặt phẳng đi qau A vuông góc với hai mặt phẳng cắt nhau cho trước (P) và (Q) là mặt phẳng đi qua A và nhận vectơ n→=[n1→,n2→ ] làm vectơ pháp tuyến; trong đó n1→ và n2→ lần lượt là vectơ pháp tuyến của (P) và (Q).
f) Mặt phẳng chứa hai đường thẳng song song (d1) và (d2) là mặt phẳng đi qua M1 và nhận vectơ [u1→,M1M2→] làm vectơ pháp tuyến, trong đó M1∈(d1),M2∈,u1→là vectơ chỉ Phương của (d1).
Mặt phẳng chứa hai đường thẳng cắt nhau (d1) và (d2) là mặt đi qua M1∈(d1) và nhận vectơ n→=[u1→,u2→ ] làm vectơ pháp tuyến, trong đó u1→,u2→ lần lượt là vectơ chỉ Phương của d1 và d2.
g) Mặt phẳng đi qua đường thẳng (d) và vuông góc với mp(P) (d không vuông góc với mp(P)) là mặt phẳng đi qua M0∈(d) và nhận vectơ [u→,n→ ] làm vectơ pháp tuyến; trong đó u→ là vectơ chỉ Phương của (d), n→ là vectơ pháp tuyến của mp(P).
Bài 5 (trang 108 sgk Hình Học 12 nâng cao):
Trong những trường hợp sau, làm thế nào để viết phương trình đường thẳng:
a) Đi qua một điểm và có vectơ chỉ phương cho trước.
b) Đi qua hai điểm phân biệt cho trước.
c) Đi qua một điểm và vuông góc với một mặt phẳng cho trước.
d) Đi qua một điểm và song song với hai mặt phẳng cắt nhau cho trước.
e) Đi qua một điểm và cắt hai đường thẳng chéo nhau cho trước.
f) Là đường vuông góc chung của hai đường thẳng chéo nhau cho trước?
Lời giải:
a) Đường thẳng đi qua M0 (x0,y0,z0 ) và nhận u→ (a,b,c) làm vectơ chỉ Phương có Phương trình là
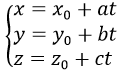
b) Đường thẳng đi qua hai điểm phân biệt A(xA,yA,zA) và B = (xB,yB,zB) là đường thẳng đi qua A(xA,yA,zA) và vectơ chỉ phương là u→=AB→=(xB-xA;yB-yA;zB-zA), nên đường thẳng AB có phương trình là
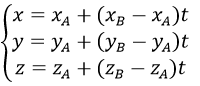
c) Đường thẳng đi qua A(xA,yA,zA) và vuông góc với mp(α):
Ax+By+Cz+D=0 là đường thẳng đi qua A(xA,yA,zA) và nhận vectơ chỉ Phương nên đường thẳng đó có Phương trình:

d) Đường thẳng đi qua A và song song với hai mặt phẳng cắt nhau (P) và (Q) là đường thẳng đi qua A và nhận vectơ n→=[n1→,n2→ ] làm vectơ chỉ phương, trong (n1→,n2→ lần lượt là vectơ pháp tuyến của (P) và (Q).
e) Để viết phương trình đường thẳng đi qua A và cắt nhau hai đường thẳng chéo nhau d1 và d2 ta làm như sau:
+ Viết phương trình mặt phẳng (P) chứa A và d1:
+ Viết Phương trình mặt phẳng (Q) chứa A và d2”
+ Giao tuyến của (P) và (Q) chính là đường thẳng cần tìm, vậy Phương trình đường thẳng cần tìm là hai hệ Phương trình của mặt phẳng P và mp(Q).
f) Cho hai đường thẳng d1 và d2 chéo nhau, đường vuông góc chung Δ của d1 và d2 là giao tuyến của hai mặt phẳng (P) và (Q), trong đó (P) chứa d1 và Δ chứa d2 và chứa Δ.
Vậy để viết Phương trình đường vuông góc chung của d1 và d2 cần viết được phương trình của (P) và (Q)
+ Mặt phẳng (P) chứa d1 và Δ là mặt phẳng đi qua M1∈d1 và nhận vectơ [n1→,[n1→,n2→ ]] làm vectơ pháp tuyến, trong đó n1→,n2→ lần lượt là vectơ chỉ phương của d1 và d2.
+ Mặt phẳng (Q) chứa d2 và Δ là mặt phẳng đi qua M2∈d2 và nhận vectơ [n2→n1→,n2→]] làm vectơ pháp tuyến.
Vậy Phương trình của Δ là hệ Phương trình của hai mẳ phẳng (P) và (Q).
Bài 6 (trang 108 sgk Hình Học 12 nâng cao):
Bằng Phương pháp tọa đố, làm thế nào để xác định được vị trí tương đối.
a) Giữa hai mặt phẳng?
b) Giữa hai đường thẳng?
Lời giải:
a) Cho hai mặt phẳng có phương trình (P): Ax+By+Cz+D=0
(Q): A’x + B’y+C’z + D’=0
Khi đó, (P) cắt (Q) <=> A: B: C ≠ A’: B’: C’
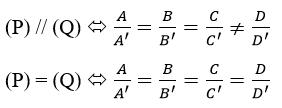
Chú ý: A: B: C ≠ A’: B’: C’ khi và chỉ khi có ít nhất hai trong ba tỉ số:
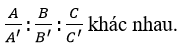
b) Cho 2 đường thẳng d1 đi qua M1(x1,y1,z1) và vectơ chỉ phương u1→(a1,b1,c1) và d2 đi qua M2 (x2,y2,z2) và vectơ chỉ phương u1→(a2,b2,c2)
Khi đó, +) d1 và d2 chéo nhau <=> u1→,u2→,M1M2→ không đồng phẳng
<=> [u1→,u2→].M1M2→ ≠ 0

Chú ý: chúng ta có thể xét vị trí tương đối của hai đường thẳng bằng cách xét số nghiệm của hệ phương trình gồm hai phương trình của hai đường thẳng.
+ Nếu hệ có 1 nghiệm thì đường thẳng cắt nhau.
+ Nếu có vô số nghiệm thì hai đường thẳng song song (nếu đồng phẳng) hoặc chéo nhau.
Bài 7 (trang 109 sgk Hình Học 12 nâng cao):
Bằng phương pháp tọa độ, làm thế nào để tính khoảng cách:
a) Từ một điểm đến một mặt phẳng.
b) Từ một điểm đén một đường thẳng
c) Giữa hai đường chéo nhau.
d) Giữ hai đường thẳng song song
e) Giữa hai mặt song song.
f) Giữa đường và mặt phẳng song song với đường thẳng đó.
Lời giải:
Cho điểm A(x0,y0,z0),mp(α):Ax+By+Cz+D=0;
Đường thẳng
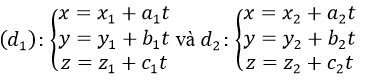
a) Khoảng cách từ điểm A đến mp(α) được xác định như sau:
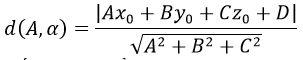
b) Khoảng cách từ điểm A đến đường thẳng (d1) là:
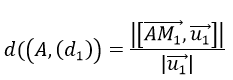
Trong đó (M1 (x1,y1,z1) là điểm trên (d1 ),(u_1 ) ⃗(a1,b1,c1) là vectơ chỉ phương của d1.
c) Giả sử d1 và d2 chéo nhau, khi đó khoảng cách giữa hai đường thẳng d1 và d2 là:
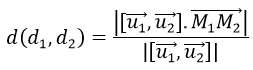
Trong đó M1∈d1và u1→ là vectơ chỉ Phương của d1
M2 ∈d2và u2→ là vectơ chỉ phương của d2
d) Giả sử d1 và d2 song song với nhau, khi đó cách từ d1 đến d2 là khoảng cách từ 1 điểm trên d1 đến đường thẳng d2, chẳng hạn:
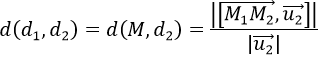
Trong đó M1∈d1,M2∈d2,u2→ là vectơ chỉ phương của đường thẳng d2.
e) Cho hai mặt phẳng (α) và (β) song song với nhau, khi đó khoảng cách giữa (α)và (β) là khoảng cách từ một điểm M bất kì thuộc (β)đến (α).
Chẳng hạn, M(x0,y0,z10 )∈(β)và (α):Ax+By+Cz+D=0
Khi đó
![]()
f) Giả sử đường thẳng d1 song song với mặt phẳng (α):Ax+By+Cz+D=0. Khi đó khoảng cách từ d1 đến mặt phẳng (α) là khoảng cách từ 1 điểm M bất kì thuộc d1 đến mp(α)
Chẳng hạn M1 (x1,y1,z1 )∈d1, khi đó ta có:
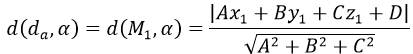
Bài 8 (trang 109 sgk Hình Học 12 nâng cao):
Trong các trường hợp sau, làm thế nào để xác định được tọa độ của điểm:
a) Là hình chiếu của một điểm trên một mặt phẳng cho trước.
b) Là hình chiếu của một điểm trên một đường thẳng cho trước.
c) Đối xứng với một điểm cho trước qua một mặt phẳng cho trước.
Lời giải:
a) Để xác định tọa độ hình chiếu của điểm A(x0,y0,z0) lên mặt phẳng (α):Ax+By+Cz+D=0 ta làm như sau:
+ Viết phương trình đường thăng Δ đi qua A và Δ vuông góc với (α), khi đó (α) có phương trình:

Trong đó vectơ n→(A,B,C) là vectơ pháp tuyến của (α) lại chính là vectơ chỉ Phương của Δ (vì Δ ⊥ (α).
+ Tìm tọa độ giao điểm của Δ và (α) là nghiệm của hệ
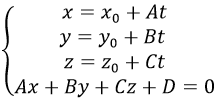
Giao điểm tìm được chính là hình chiếu của A lên mp(α).
b) Để tìm tọa độ hình chiếu của điểm A(x0,y0,z0) lên đường thẳng
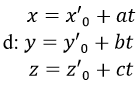
ta làm như sau:
+ viết Phương trình mặt phẳng đi qua A(x0,y0,z0) và vuông góc với d, đó là mặt phẳng đi qua A(x0,y0,z0) và nhận vectơ chỉ phương của d là u→(a,b,c) là vectơ pháp tuyến, nên mặt phẳng đó có phương trình là: a(x-x0 )+b(y-y0 )+c(z-z0 )=0.
+ Tìm tọa độ giao điểm của đường thẳng d và mặt phẳng trên ta được hình chiếu vuông góc của A lên d.
c) Để tìm điểm đối xứng A’ của A(x0,y0,z0) qua mặt phẳng (α):Ax+By+Cz+D=0 ta làm như sau:
+ Tìm hình chiếu vuông góc H của A lên mp(α):
+ Vì A’ đối xứng với A lên H là trung điểm của đoạn AA’, từ đó ta tìm được tọa độ A’ qua hệ thức: