Bài 1 (trang 80 SGK Hình học 12): Viết phương trình mặt phẳng:

Lời giải

Bài 2 (trang 80 SGK Hình học 12): Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(2; 3; 7), B(4; 1; 3)
Lời giải:

Bài 3 (trang 80 SGK Hình học 12):
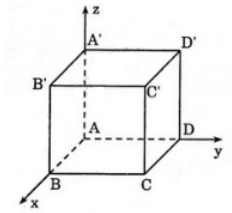
a) Lập phương trình của các mặt phẳng tọa độ Oxy, Oyz và Ozx
b) Lập phương trình của các mặt phẳng đi qua điểm M(2; 6; -3) và lần lượt song song với các mặt phẳng tọa độ.
Lời giải:
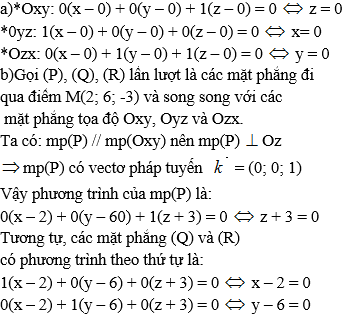
Bài 4 (trang 80 SGK Hình học 12): Lập phương trình mặt phẳng:
a)Chứa trục Ox và điểm P(4; -1; 2)
b)Chứa trục Oy và điểm Q(1; 4; -3)
c)Chứa trục Oz và điểm R(3; -4; 7)
Lời giải:

Bài 5 (trang 80 SGK Hình học 12): Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0; 4), D(4; 0; 6)
a)Hãy viết phương trình của các mặt phẳng (ACD) và (BCD)
b)Hãy viết phương trình mặt phẳng (α) đi qua cạnh AB và song song với cạnh CD.
Lời giải:

Bài 6 (trang 80 SGK Hình học 12): Hãy viết phương trình mặt phẳng (α) đi qua điểm M(2; -1; 2) và song song với mặt phẳng (β) : 2x – y + 3z + 4 = 0
Lời giải:
Vì mặt phẳng (α) song song với mặt phẳng ( β) : 2x – y + 3z + 4 = 0 nên phương trình của mp(α) có dạng 2x – y + 3z + D = 0
Vì M(2; -1; 2) ∈ mp(α) nên 4 + 1 + 6 + D = 0 <=> D = -11
Vậy phương trình của mp(α) là: 2x – y + 3z – 11= 0
Bài 7 (trang 80 SGK Hình học 12): Lập phương trình mặt phẳng (α) qua hai điểm A(1; 0; 1), B(5; 2; 3) và vuông góc với mặt phẳng ( β) : 2x – y + z – 7 = 0
Lời giải:

Bài 8(trang 81 SGK Hình học 12): Xác định các giá trị của m và n để mỗi cặp mặt phẳng sau đây là một cặp mặt phẳng song song với nhau;
a)2x + my + 3z – 5 = 0 và nx – 8y – 6z + 2 =0
b)3x – 5y + mz – 3 = 0 và 2x + ny – 3z + 1 = 0
Lời giải:

Bài 9 (trang 81 SGK Hình học 12): Tính khoảng cách từ điểm A(2; 4; -3) lần lượt đến các mặt phẳng sau:a) 2x – y + 2z – 9 = 0 (α)b) 12x – 5z + 5 = 0 ( β)c) x = 0 ( γ;)
Lời giải
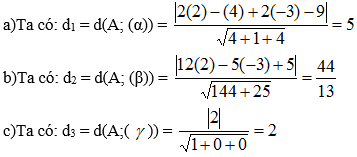
Bài 10 (trang 81 SGK Hình học 12): giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1.
a)Chứng minh hai mặt phẳng (AB’D’) và (BC’D) song song.
b)Tính khoảng cách giữa hai mặt phẳng nói trên.
Lời giải: