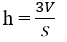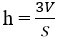
Bài 1 (trang 30 sgk Hình Học 12 nâng cao):
Khối lăng trụ n – giác có bao nhiêu đỉnh, bao nhiêu cạnh và bao nhiêu mặt? Khối chóp n – giác có bao nhiêu đỉnh, bao nhiêu cạnh và bao nhêu mặt?
Lời giải:
– Khối lăng trụ n – giác có 2n đỉnh, 3n cạnh và n + 2 mặt.
– Khối chóp n – giác có n + 1 đỉnh, 2n cạnh và n + 1 mặt.
Bài 2 (trang 30 sgk Hình Học 12 nâng cao):
Những khối đa diện đều nào có mặt là tam giác đều? Mỗi đỉnh của nó là đỉnh chung của bao nhiêu mặt?
Lời giải:
Các khối đa diện nhiều loại{3; p} có mỗi mặt tam giác đều (trong đó p =3, p =4 hoặc p =5).
– Khối đa diện đều loại {3; 3} là tứ diện đều, mỗi đỉnh là đỉnh chung của 3 cạnh.
– Khối đa diện đều loại {3, 4} là khối 8 mặt đều, mỗi đỉnh là đỉnh chung của 4 cạnh.
– Khối đa diện đều loại {3, 5} là khối 20 mặt đều, mỗi đỉnh là đỉnh chung của 5 cạnh.
Bài 3 (trang 30 sgk Hình Học 12 nâng cao):
Nếu biết thể tích của một khối chóp và diện tích đáy của nó thì có thể biết được chiều cao của khối chóp đó hay không.
Lời giải:
Nếu một khối chóp có thể tích là V và diện tích mặt đáy của nó là S thì chiều cao của nó được tính theo công thức
Bài 4 (trang 30 sgk Hình Học 12 nâng cao):
Nếu mỗi kích thước hình hộp chữ nhật được tăng lên k lần thì thể tích của khối chóp đó hay không?
Lời giải:
Nêu mỗi kích thước của 1 hình hộp chữ nhạt được tăng lên k lần thì thể tích khối hộp đó được tăng lên k3 lần.
Bài 5 (trang 30 sgk Hình Học 12 nâng cao):
Hình tứ diện đều, hình lập phương, hình bát diện đều có những mặt phẳng đối xứng nào?
Lời giải:
– Hình tứ diện đều có 6 mặt phẳng đối xứng. đó là các mặt phẳng đi qua một cạnh và trung điểm của cạnh đối diện.
– Hình lập phương có 9 mặt phẳng đối xứng, gồm 3 mặt phẳng trung trực của 3 cạnh cùng xuất phát tại một đỉnh; các mặt phẳng xác định bởi một cặp cạnh đối diện của hình lập phương.
– Hình bát diện đều ABC.DEF có 9 mặt phẳng đối xứng gồm: (ABCD), (BEDF), (AECF), mặt phẳng phẳng trung trực của các cạnh AB, AD, AF, BE, BF.
Bài 6 (trang 30 sgk Hình Học 12 nâng cao):
Nếu tỉ số các cạnh tương ứng của hai tứ diện đồng dạng bằng k thì tỉ số thể tích của hai khối tứ diện ấy bằng bao nhiêu?
Lời giải:
Nêu tỉ số các cạnh tương ứng của hai tứ diện đồng dạng k thì tỉ số thể tích của hai khối tứ diện ấy bằng k3.