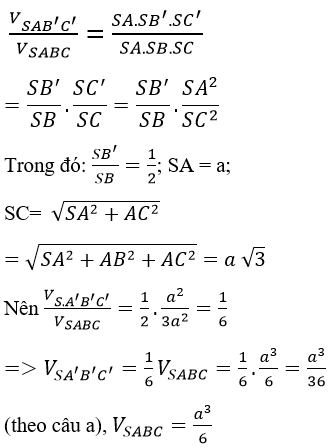
Bài 1 (trang 30 sgk Hình Học 12 nâng cao):

Cho tứ diện ABCD có thể tích bằng V. Gọi B’ và D’ lần lượt là trung điểm của AB và AD. Mặt phẳng (CB’D’) chia khối tứ diện thành 2 phần. Thể tích mỗi phần đó.

Lời giải:

Mặt phẳng (CB’D’) chia khối tứ diện ABC thành hai khối chóp là AB’C’D’ và C.BB’D’D ta có:

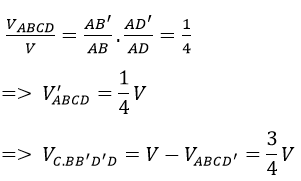
Bài 2 (trang 31 sgk Hình Học 12 nâng cao):

Cho khối hộp ABCD.A’B’C’D’. Chứng minh rằng sau trung điểm của sáu cạnh AB, BC, CC’, C’D’, D’A’ và A’A nằm trên một mặt phẳng và mặt phẳng đó chia khối lập phương thành hai phần có thể tích bằng nhau.

Lời giải:

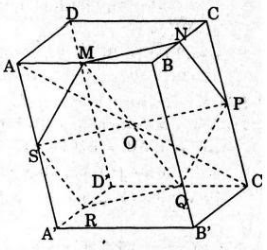
Gọi O là giao điểm của các đường chéo của hình hộp. ta có O là trung điểm của AC’, tứ giác AMC’Q là hình bình hành nên O là trung điểm của MQ.

Vậy O, M, Q thẳng hàng. Hơn nữa MN, SP, RQ đôi một song song và lần lượt đi qua O, M, Q nên M, N, P, Q, R, S cùng nằm trên mp(α) đi qua O (và mp(α) // (ACD’)).

Ta thấy D là trung điểm của AC’, BD’, A’C, B’D, MQ, NR, SP nên (α) chia khối hộp thành hai phần là ảnh của nhau qua V^0,-1 (hay phép đối xứng tâm O) do đó chung ta có thể tích bằng nhau.

Bài 3 (trang 31 sgk Hình Học 12 nâng cao):

Cho khối tứ diện ABCD, E và F lần lượt là trung điểm của hai cạnh AB và CD. Hai mp(ABF) và (CDE) chia khối tứ diện ABCD thành 4 khối tứ diện.

a) Kể tên bốn khối tứ diện.

b) Chứng tở rằng bốn khối tứ diện đó có thể tích bằng nhau.

c) Chứng tỏ rằng nếu ABCD là khối tứ diện đều thì bốn khối tứ diện nói trên bằng nhau.

Lời giải:

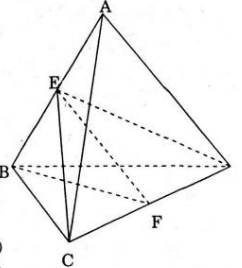
a) 4 khối tứ diện đó là: BCEF, ACEF, BDEF, ADEF.

b) Do E là trung điểm của AB nên S_ΔBEF=S_ΔAEF

=> V_CBEF=V_CAEF và V_DBEF=V_DAEF

Hay V_BCEF=V_ADEF

Và V_BDEF=V_ADEF     (1)

Tương tự S_ΔCEF=S_ΔDEF

=> V_ACEF=V_ADEF    (2)

Từ (1) và (2)

V_BCEF=V_ADEF=V_BDEF=V_ADEF

c) Nếu ABCD là khối tứ diện đều thì (CED), (ABF) là các mặt phẳng đối xứng của tứ diện.

Cách 1. Ta có: phép đối xứng qua (ABF) biến tứ diện BCEF, ACEF thành ADEF (1), phép đối xứng qua (CED) biến DBEF thành DAEF hay ADEF (2)

Từ (1) và (2) suy ra các tứ diện BCEF, ACEF, ADEF, BDEF bằng nhau.

Cách 2. Thực hiện phép đối xứng qua mặt phẳng (ABF).

Ta có: tứ diện BCEF biến BDEF, AECF biến thành AEDF (1) do EF là trục đối xứng qua đường thẳng EF biến tứ diện BCEF thành ADEF (2)

Từ (1) và (2) đpcm.

Bài 4 (trang 31 sgk Hình Học 12 nâng cao):

Cho khối lăng trụ đứng ABC.A’B’C’ có diện tích đáy bằng S vì AA’ = h. Mặt phẳng (P) cắt các cạnh AA’, BB’, CC’ tạo A₁,B₁,C₁. Biết AA₁=a₁ BB₁=b₁ CC₁=c

a) Tính thể tích hai phần khối lăng trụ được chia bởi (P).

b) Với điều kiện nào của a, b, c thì thể tích hai phần đó bằng nhau.

Lời giải:

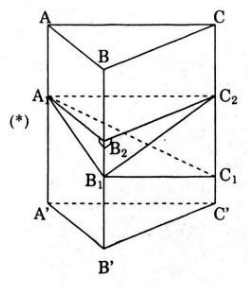
a) Cách 1. Giải sử a≤b≤c. Lấy B₂,C₂ lần lượt trên cạnh BB’, CC’ sap cho BB₂=a,CC₂=a=>B₁B₂=b-a ,C₁C₂=c-a.

V_ABCA1B2C1=V_ABC.A1B2C2+V_A1B1B2C1C3=a.S+V_A1B1B2C2C3

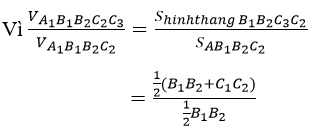
(hình thang và tam giác có cùng chiều cao)

Thay vào (*) ta được:

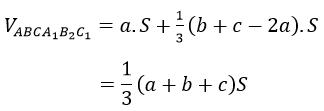
Tương tự:

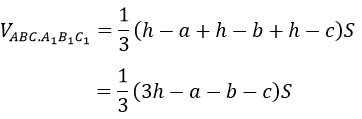
Cách 2: không làm mất tính tổng quát, giả sử a≤b≤c.

Trên cạnh BB’ lấy B₂ sao cho BB₂=a

=> B₁B₂=b-a

Trên cạnh CC’ lấy C₂ sao cho CC₂=a

=> C₁C₂=c-a

Ta có: V_ABC.A1B1C1=V_ABC.A1B2 C2+V_A1B2C2B1+V_A1B1C2C1

Trong đó:

V_ABC.A1B2C2=AA₁.S_ΔABC=a.S (1)

(vì B₁B₂ ⊥ (A₁B₂C₂ ).ΔA₁B₂C₂=ΔABC)

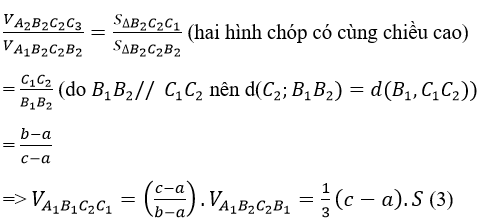
Thay (1), (2) và (3) và (*) ta được:

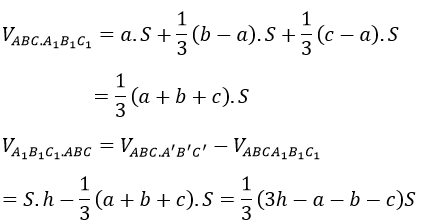
Bài 5 (trang 31 sgk Hình Học 12 nâng cao):

Cho khối lăng trụ đều ABC.A’B’C’ và M là trung điểm của cạnh AB. Mặt phẳng (B’C’M) chia khối trụ thành hai phần. Tính tỉ số thể tích hai phần đó.

Lời giải:

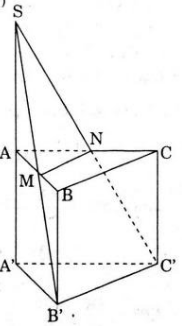
Gọi V₁ là thể tích của phần chứa cạnh AA’, V₂ là thể tích phần còn lại

S là diện tích đáy A’B’C’, h là chiều cao của lăng trụ và V là thể tích của lăng trụ. Do BC//B’C’ nên (ABC) cắt (MB’C’) theo giao tuyến là đường thẳng d qua M và d // BC.

Gọi N = d ∩ AC. Dể thấy A’A, B’M, C’N đồng quy tại S.

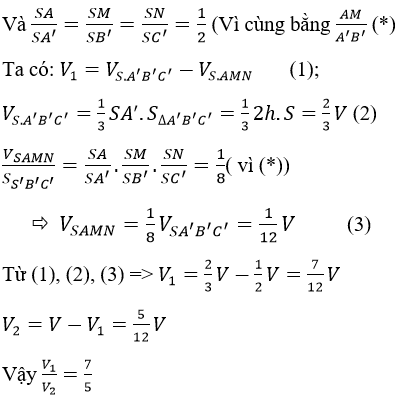
Bài 6 (trang 31 sgk Hình Học 12 nâng cao):

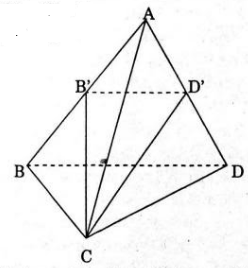
Cho khối chóp S.ABC có đường cao SA = a, đáy là tam giác cân AB=BC = a. Gọi B’ là trung điểm của SB, C’ là chân đường cao hạ từ A của ΔSAC.

a) Tính thể tích khối chóp S.ABC

b) Chứng minh rằng SC ⊥ (AB’C’)

c) Tính thể tích khối chóp S.A’B’C’

Lời giải:

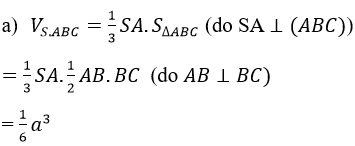
Cách 1. Ta có: BC⊥AB (gt)

BC⊥SA (do SA⊥(ABC))

=>BC⊥(SAB)=>SB là hình chiếu của SC trên (SAB)

Mặt khác: SA = AB (do đều bằng a) và B’ là trung điểm của SB nên AB’⊥SB . vậy AB’⊥SC (1) (định lí 3 đường vuông góc)

Lại có, C’ là hình chiếu của A trên SC nên AC’⊥ SC (2)

Từ (1), (2) suy ra SC⊥(AB’C’)

Cách 2.

Ta có: BC ⊥(SAB) vì (BC ⊥AB,BC⊥SA do SA ⊥(SAB) => BC ⊥AB’

Lại có SB ⊥AB'(trung tuyến trong tam giác cân)

Vậy AB’ ⊥(SBC)=> AB’⊥SC (1)

Mặt khác C’ là hình chiếu của A trên SC nên AC’ ⊥ SC (2)

Từ (1), (2) suy ra SC ⊥(AB’C’ )

Tính V_{S.A’B’C’}?

Cách 1. Vì SC’⊥AB’C’ nên:

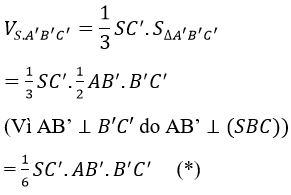
Ta có: SC’ = (SA²)/SC (do AC’ là đường cao của trong tam giác vuông SAC)

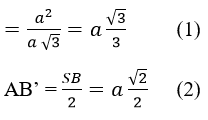
(trung tuyến trong tam giác vuông)

B’C’ = √(AC’²-AB² ) (do AB’ ⊥ B’C’)

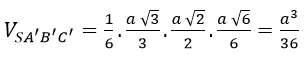
Thay (1), (2), (3) vào (*) ta được:

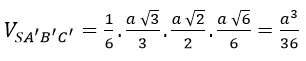
Nhận xét:

Ta có: AB’⊥(SBC) nên có thể lấy V = (1/3)AB’.S_ΔSB’C’=(1/6). AB’.B’ C’.SC’ rồi giải như cách 1.

Cách 2: ta có:

Comments

comments