Bài 1 (trang 7 sgk Hình Học 12 nâng cao):
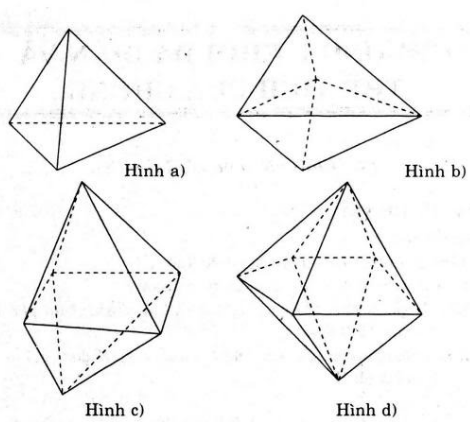
Chứng minh rằng nếu khối đa diện có các mặt là tam giác thì số mặt phải là số chẵn. Hãy chỉ ra những khối đa diện như thế với số mặt bằng 4, 6, 8, 10.
Lời giải:
– Giải sử khối đa diện đã cho có M mặt và C cạnh.
Vì mỗi mặt có 3 cạnh nên M mặt có 3M cạnh, nhưng mỗi cạnh lại có hai lưng cho 2 mặt nên có 2C = 3M, suy ra M chẵn. vậy nếu khối đa diện có các mặt làm tam giác thì số mặt phải là số chẵn.

– Khối a) khối tứ diện có 4 mặt là tam giác.
– Hình b) khối 6 mặt là tam giác.
– Hình c) khối 8 mặt là tam giác.
– Hình d) khối 10 mặt là tam giác
Bài 2 (trang 7 sgk Hình Học 12 nâng cao):
Chứng minh rằng nếu khối đa diện mà mỗi đỉnh là đỉnh chung của cạnh thì số đỉnh phải là số chẵn.
Lời giải:
Gọi Đ, C lần lượt là số đỉnh, số cạnh của đa diện.
Vì mỗi đỉnh là đỉnh chung của ba cạnh nên Đ đỉnh có 3 Đ cạnh, như mỗi cạnh là cạnh chung của 2 đỉnh.
Vậy 2C = 3Đ. Từ đó suy ra Đ là số chẵn.
Bài 3 (trang 7 sgk Hình Học 12 nâng cao):
Chứng minh rằng khối đa diện có các mặt là tam giác và m là đỉnh chung của 3 cạnh thì đó là khối tứ diện.
Lời giải:
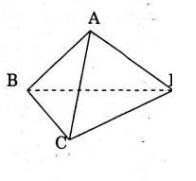
Gọi A là một đỉnh của khối đa diện. A là đỉnh chung của 3 cạnh AB, AC, AD. Mặt chứa cạnh AB, AC, AD phải là ΔABC, tương tự ΔACD, ΔADB cũng là các mặt của đa diện. vậy xuất phát từ đỉnh D của đa diện có các cạnh DC, DB, nên mặt chứa cạnh DB và Dc phải là ΔBCD dây là mặt thứ 4 của đa diện. Từ đó suy ra kết quả bài toán.
Bài 4 (trang 7 sgk Hình Học 12 nâng cao):
Hãy phân tích một khối hộp thành 5 khối tứ diện.
Lời giải:
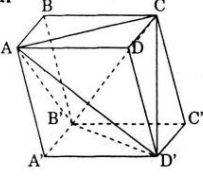
Khối hộp ABCDA’B’C’D’ được chia thành 5 khối tứ diện CB’C’D’; BCB’A; A’B’D’; DACD’; B’ACD’; bởi các mặt phẳng (CB’D’), (ACB’), (ABD’), (ACD’).
Bài 5 (trang 7 sgk Hình Học 12 nâng cao):
Hãy phân tích khối tứ diện thành bốn khối tứ diện bởi hai mặt phẳng.
Lời giải:
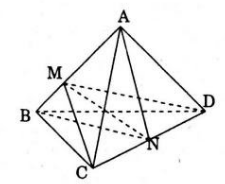
Gọi M, N là hai điểm trên cạnh AB, CD (khác hai đầu nút). Khi đó hai mặt phẳng (ABN) và (CMD) chia khối tứ diện ABCD thành bố khối tứ diện: CBMN, DBMN, CAMN, DAMN.