Trả lời câu hỏi Toán 10 Đại số Bài 3 trang 63: Cặp (1; -2) có phải là một nghiệm của phương trình 3x – 2y = 7 không ? Phương trình đó còn có những nghiệm khác nữa không ?
Lời giải
Ta có: 3.1-2.(-2) = 7 ⇒ Cặp (1; -2) là một nghiệm của phương trình 3x – 2y = 7
Các nghiêm khác của phương trình đó là: (3; 1); (-1; -5)
Trả lời câu hỏi Toán 10 Đại số Bài 3 trang 64: Hãy biểu diễn hình học tập nghiệm của phương trình 3x – 2y = 6.
Lời giải
3x – 2y = 6 ⇔ y = 3/2x – 3
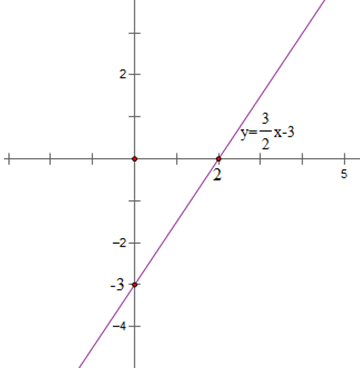
Tập nghiệm của phương trình 3x – 2y = 6 là đường thẳng y = 3/2x-3
Trả lời câu hỏi Toán 10 Đại số Bài 3 trang 64: a) Có mấy cách giải hệ phương trình
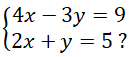
b) Dùng phương pháp cộng đại số để giải hệ phương trình
Có nhận xét về nghiệm của hệ phương trình này ?
Lời giải
a) Có 2 cách là cộng đại số và thế
b)
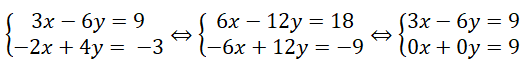
⇒ hệ phương trình vô nghiệm do phương trình 0x + 0y = 9 vô nghiệm.
Nhận xét: Hệ phương trình trên vô nghiệm.
Trả lời câu hỏi Toán 10 Đại số Bài 3 trang 65: Hãy giải hệ phương trình (5).
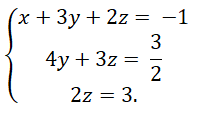
Lời giải
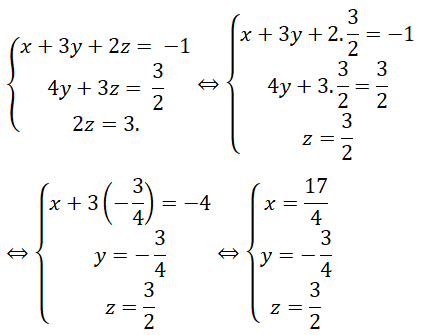
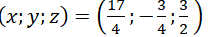
Vậy hệ phương trình có nghiệm duy nhất
Bài 1 (trang 68 SGK Đại số 10): Cho hệ phương trình
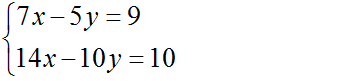
Tại sao không cần giải ta cũng kết luận được hệ phương trình này vô nghiệm.
Lời giải:
Ta có:
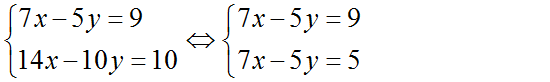
Không tồn tại cặp nghiệm (x ; y) nào thỏa mãn hệ phương trình trên nên hệ phương trình đã cho vô nghiệm.
Bài 2 (trang 68 SGK Đại số 10): Giải các hệ phương trình
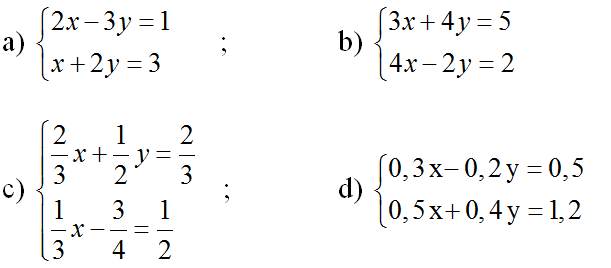
Lời giải:
Cách 1: Cộng đại số.
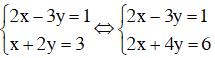
a) (Nhân cả hai vế phương trình thứ hai với 2)
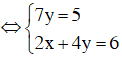
(Lấy phương trình thứ hai trừ đi phương trình thứ nhất).
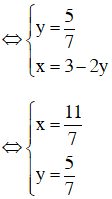
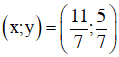
Vậy hệ phương trình có nghiệm
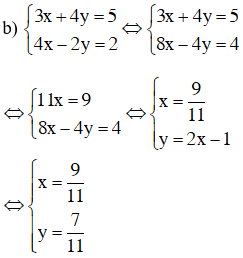
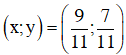
Vậy hệ phương trình có nghiệm
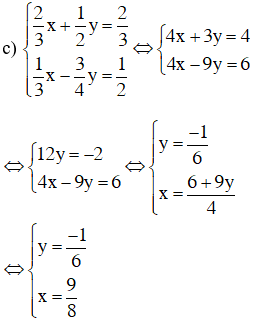
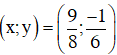
Vậy hệ phương trình có nghiệm
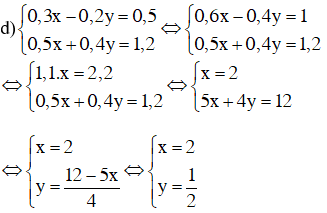
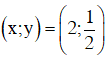
Vậy hệ phương trình có nghiệm
Cách 2: Sử dụng phương pháp thế.
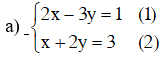
Từ (2) suy ra x = 3 – 2y, thế vào phương trình (1) ta được:
2.(3 – 2y) – 3y = 1
⇔ 6 – 4y – 3y = 1
⇔ 7y = 5
⇔ y = 5/7.
Thay y = 5/7 vào x = 3 – 2y ta được : x = 3 – 2.5/7 = 11/7.
Vậy hệ phương trình có nghiệm (x ; y) = (11/7 ; 5/7).
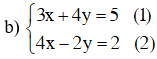
Từ (2) rút ra được y = 2x – 1, thế vào phương trình (1) ta được
3x + 4.(2x – 1) = 5
⇔ 3x + 8x – 4 = 5
⇔ 11x = 9
⇔ x = 9/11
Thay vào phương trình y = 2x – 1 ta được y = 2.9/11 – 1 = 7/11.
Vậy hệ phương trình có nghiệm (x; y) = (9/11; 7/11)
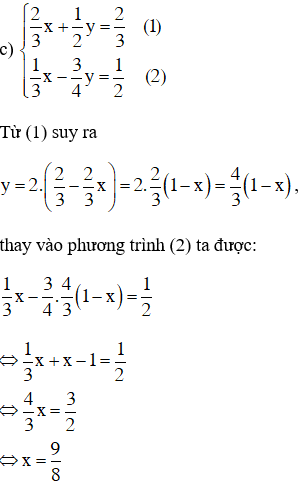
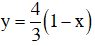
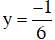
Thay vào phương trình ta tìm được
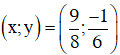
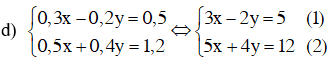
Vậy hệ phương trình có nghiệm
Từ (1) rút ra 2y = 3x – 5, thay vào phương trình (2) ta được:
5x + 2.(3x – 5) = 12
⇔ 5x + 6x – 10 = 12
⇔ 11x = 22
⇔ x = 2.
Thay x = 2 vào phương trình 2y = 3x – 5 ta được 2y = 1 ⇔ y = 1/2.
Vậy hệ phương trình có nghiệm (x ; y) = (2 ; 1/2)
Kiến thức áp dụng
Có hai cách giải hệ phương trình là thế hoặc cộng đại số.
Bài 3 (trang 68 SGK Đại số 10): Hai bạn Vân và Lan đến cửa hàng mua trái cây. Bạn Vân mua 10 quả quýt, 7 quả cam với giá tiền là 17800 đồng. Bạn Lan mua 12 quả quýt, 6 quả cam hết 18000 đồng. Hỏi giá tiền mỗi quả quýt và quả cam hết bao nhiêu ?
Lời giải:
Gọi x và y lần lượt là giá tiền mỗi quả quýt và mỗi quả cam. (x > 0; y > 0)
Vân mua 10 quả quýt, 7 quả cam hết 17800 đồng nên ta có:
10x + 7y = 17800
Lan mua 12 quả quýt, 6 quả cam hết 18000 đồng nên ta có:
12x + 6y = 18000
Từ đó ta có hệ:
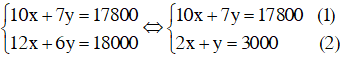
Từ (2) rút ra được y = 3000 – 2x, thay vào (1) ta được :
10x + 7.(3000 – 2x) = 17800
⇔ 10x + 21000 – 14x = 17800
⇔ 4x = 3200 ⇔ x = 800 (thỏa mãn)
Thay x = 800 vào y = 3000 – 2x ta được y = 1400 (thỏa mãn)
Vậy giá tiền một quả quýt là 800đ và giá tiền một quả cam là 1400đ.
Kiến thức áp dụng
Đây là dạng bài giải bài toán bằng cách lập hệ phương trình đã học ở lớp 8.
Bước 1: Lập hệ phương trình:
+ Chọn các ẩn số và đặt điều kiện thích hợp cho các ẩn số.
+ Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
+ Lập hệ phương trình biểu thị mối quan hệ giữa các đại lương.
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không rồi kết luận.
Bài 4 (trang 68 SGK Đại số 10): Có hai dây chuyền may áo sơ mi. Ngày thứ nhất cả hai dây chuyền may được 930 áo. Ngày thứ hai day chuyền thứ nhất tăng năng suất 18%, dây chuyền thứ hai tăng năng suất 15% nên cả hai dây chuyền này may được 1083 áo. Hỏi trong ngày thứ nhất mỗi dây chuyền may được bao nhiêu áo sơ mi ?
Lời giải:
Gọi số áo sơ mi may được trong ngày thứ nhất của dây chuyền thứ nhất và dây chuyền thứ hai lần lượt là x và y. (x > 0; y > 0)
Ngày thứ nhất cả hai dây chuyền may được 930 áo nên ta có: x + y = 930.
Ngày thứ hai:
dây chuyền thứ nhất tăng năng suất 18% nên may được x + 18%.x = 1,18.x áo
dây chuyền thứ hai tăng năng suất 15% nên may được y + 15%.y = 1,15y áo
Cả hai dây chuyền may được 1083 áo nên ta có: 1,18x + 1,15y = 1083.
Ta có hệ phương trình
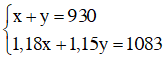
Giải hệ phương trình ta được: x = 450, y = 480
Vậy số áo sơ mi dây chuyền thứ nhất và dây chuyền thứ hai may được trong ngày thứ nhất lần lượt là 450 (áo) và 480 (áo).
Kiến thức áp dụng
Đây là dạng bài giải bài toán bằng cách lập hệ phương trình đã học ở lớp 8.
Bước 1: Lập hệ phương trình:
+ Chọn các ẩn số và đặt điều kiện thích hợp cho các ẩn số.
+ Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
+ Lập hệ phương trình biểu thị mối quan hệ giữa các đại lương.
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không rồi kết luận.
Bài 5 (trang 68 SGK Đại số 10): Giải các hệ phương trình
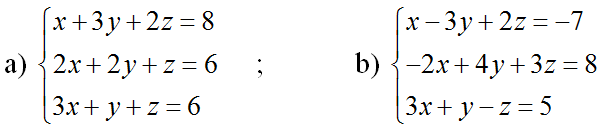
Lời giải:
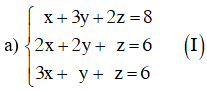
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số ta có:
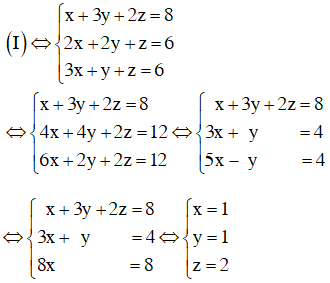
Vậy hệ phương trình có nghiệm (x; y; z) = (1; 1; 2).
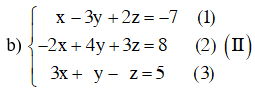
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (1) với (3) rồi trừ đi phương trình (3) ta được:
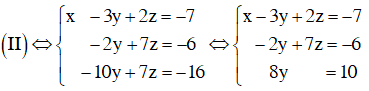
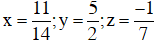
Giải hệ phương trình trên ta được
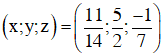
Vậy hệ phương trình có nghiệm
Kiến thức áp dụng
Để giải hệ ba phương trình bậc nhất ba ẩn, ta khử dần từng ẩn số để đưa hệ phương trình về dạng hệ tam giác, từ đó tìm ra nghiệm của hệ phương trình.
Bài 6 (trang 68 SGK Đại số 10): Một cửa hàng bán áo sơ mi, quần nam và váy nữ. Ngày thứ nhất bán được 21 áo, 21 quần và 18 váy, doanh thu là 5.349.000 đồng. Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5.600.000 đồng. Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu là 5.259.000 đồng. Hỏi giá bán mỗi áo, mỗi quấn và mỗi váy là bao nhiêu ?
Lời giải:
Gọi x, y, z (đồng) lần lượt là giá tiền mỗi áo, quần và váy (0 < x, y, z < 5259000).
Ngày thứ nhất bán được 21 áo, 21 quần và 18 váy, doanh thu là 5.349.000 đồng nên ta có:
12x + 21y + 18z = 5.349.000
Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5.600.000 đồng nên ta có:
16x + 24y + 12z = 5.600.000
Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu là 5.259.000 đồng nên ta có:
24x + 15y + 12z = 5.259.000
Từ đó ta có hệ phương trình:
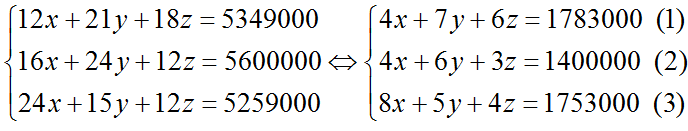
Lấy (1) – (2) ta được : y + 3z = 383000.
Nhân 2 vào hai vế của (1) rồi trừ đi (3) ta được: 9y + 8z = 1813000
Ta có hệ phương trình:
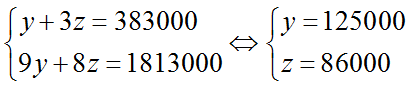
Thay y = 125000, z = 86000 vào (1) ta được x = 98000.
Vậy: Giá bán mỗi áo là: 98.000 đồng.
Giá bán mỗi quần là: 125.000 đồng.
Giá bán mỗi váy là: 86.000 đồng.
Kiến thức áp dụng
Đây là dạng bài giải bài toán bằng cách lập hệ phương trình đã học ở lớp 8.
Bước 1: Lập hệ phương trình:
+ Chọn các ẩn số và đặt điều kiện thích hợp cho các ẩn số.
+ Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;
+ Lập hệ phương trình biểu thị mối quan hệ giữa các đại lương.
Bước 2: Giải hệ phương trình
Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không rồi kết luận.
Bài 7 (trang 68 SGK Đại số 10): Giải các hệ phương trình sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ hai)
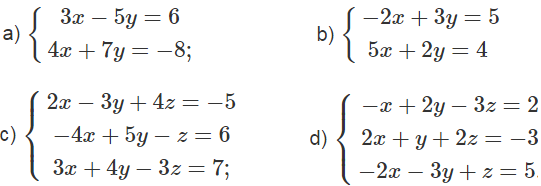
Hướng dẫn cách giải câu a)
Nếu sử dụng máy tính CASIO fx-500 MS ta ấn liên tiếp dãy các phím
thấy hiện ra trên màn hình x = 0,048780487
Ấn tiếp phím = ta thấy trên màn hình hiện ra y = -1,170731707
Làm tròn kết quả đến chữ số thập phân thứ hai ta được nghiệm gần đúng của hệ phương trình là
(x; y) ≈ (0,05; -1,17)
Hướng dẫn cách giải câu c)
Nếu sử dụng máy tính CASIO fx-500 MS ta ấn liên tiếp dãy các phím
thấy hiện ra trên màn hình x = 0,217821782
Ấn tiếp phím = ta thấy trên màn hình hiện ra y = 1,297029703
Ấn tiếp phím = ta thấy trên màn hình hiện ra z = -0,386138613
Vậy nghiệm gần đúng của hệ phương trình là (làm tròn kết quả đến chữ số thập phân thứ hai)
(x; y; z) ≈ (0,22; 1,30; -0,39)
Lời giải:
* Đối với máy tính CASIO f(x)–500MS các bạn ấn như trên hướng dẫn.
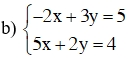
Để giải hệ phương trình trên, ta ấn các dãy phím sau :
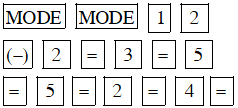
Màn hình hiện x = 0.1052631579
Ấn tiếp thì màn hình hiện y = 1.736842105
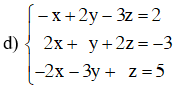
Để giải hệ phương trình trên ta ấn các dãy phím sau :
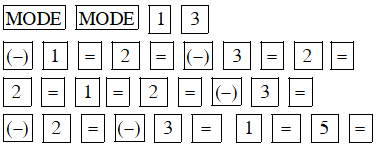
Màn hình hiển thị x = –4
Ấn tiếp thì màn hình hiển thị y = 1.571428571
Ấn tiếp thì màn hình hiển thị z = 1.714285714
* Đối với các loại máy tính CASIO fx–570 và các loại máy VINACAL, để giải hệ phương trình các bạn ấn
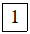
sau đó ấn nếu như giải hệ hai phương trình bậc nhất hai ẩn
ấn nếu như giải hệ ba phương trình bậc nhất ba ẩn.
Sau đó nhập các hệ số của hệ phương trình như trên.
Kết quả sẽ hiện dưới dạng phân số, để kết quả hiện dưới dạng số thập phân, các bạn dùng phím
