![[Giải Toán 10] Chương 1: Vectơ/ Bài 3: Tích của vectơ với một số [Giải Toán 10] Chương 1: Vectơ/ Bài 3: Tích của vectơ với một số](https://lop12.edu.vn/wp-content/uploads/2019/10/c3.png)
Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 14: Cho vectơ a→ ≠ 0→. Xác định độ dài và hướng của vectơ a→ + a→.
Lời giải
Ta có: a→ + a→ = 2a→
Độ dài của vecto a→ + a→ bằng 2 lần độ dài của vecto a→
Hướng của vecto a→ + a→ cùng hướng với vecto a→
Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 14: Tìm vectơ đối của các vectơ ka→ và 3a→ – 4b→.
Lời giải
Vectơ đối của các vectơ ka→ là vectơ -ka→
Vectơ đối của các vectơ 3a→ – 4b→ là vecto -3a→ + 4b→0→
Trả lời câu hỏi Toán 10 Hình học Bài 3 trang 15: Hãy sử dụng mục 5 của bài 2 để chứng minh các khẳng định trên.
Lời giải
a) Với điểm M bất kì, ta có:

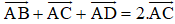
Bài 1 (trang 17 SGK Hình học 10): Cho hình bình hành ABCD. Chứng minh rằng:
Lời giải:
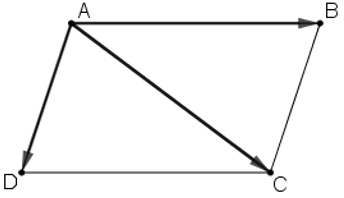
ABCD là hình bình hành
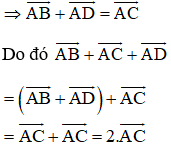
Kiến thức áp dụng
+ Quy tắc hình bình hành:
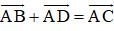
Nếu ABCD là hình bình hành thì
+ Với vec tơ a→ bất kì và hai số h, k thì:
h.a→ + k.a→ = (h + k).a
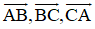
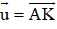
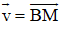
Bài 2 (trang 17 SGK Hình học 10): Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ theo hai vec tơ và
Lời giải:
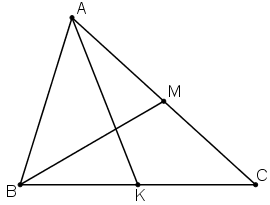
+ K là trung điểm của BC nên ta có:
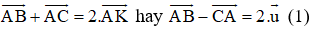
+ M là trung điểm AC nên ta có:
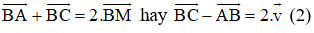
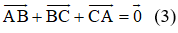
+ Lại có
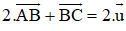
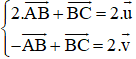
Cộng (1) với (3) ta được , kết hợp với (2) ta được hệ phương trình:
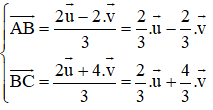
Giải hệ phương trình ta được
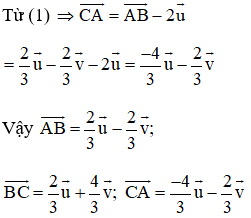
Kiến thức áp dụng
+ Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có :
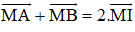
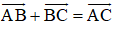
+ Quy tắc ba điểm: với mọi điểm A, B, C bất kì.
+ Giải hệ phương trình.
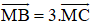
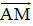
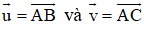
Bài 3 (trang 17 SGK Hình học 10): Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho . Hãy phân tích vec tơ theo hai vec tơ
Lời giải:
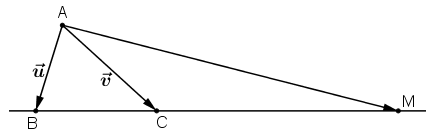
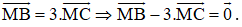
Ta có:
Theo quy tắc ba điểm ta có:
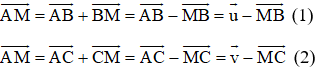
Lấy (1) trừ 3 lần (2) ta được:
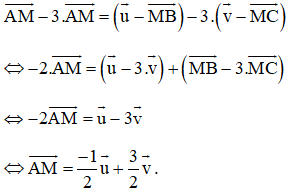
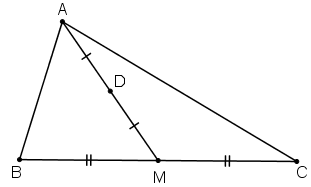
Bài 4 (trang 17 SGK Hình học 10): Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM.
Chứng minh rằng:
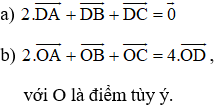
Lời giải:

Kiến thức áp dụng
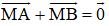
+ M là trung điểm của đoạn thẳng AB
+ M là trung điểm của đoạn thẳng thì với mọi điểm D ta có
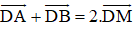
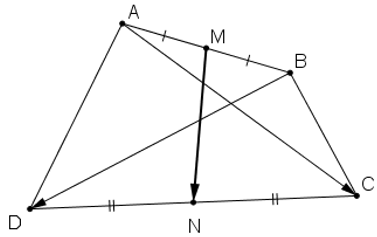
Bài 5 (trang 17 SGK Hình học 10): Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD.
Chứng minh rằng:
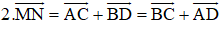
Lời giải:


Kiến thức áp dụng
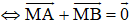
+ M là trung điểm của đoạn thẳng AB
+ M là trung điểm của đoạn thẳng thì với mọi điểm D ta có
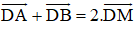
Bài 6 (trang 17 SGK Hình học 10): Cho hai điểm phân biệt A và B. Tìm điểm K sao cho
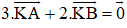
Lời giải:
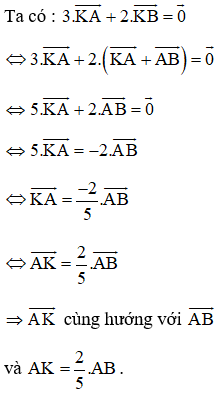
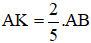
hay K là điểm nằm trên đoạn thẳng AB và
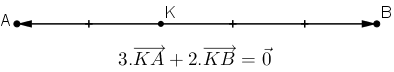
Bài 7 (trang 17 SGK Hình học 10): Cho tam giác ABC. Tìm điểm M sao cho
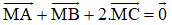
Lời giải:
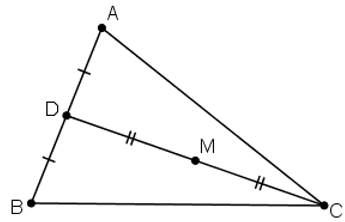
Gọi D là trung điểm AB.
Khi đó với mọi điểm M ta có :

⇔ M là trung điểm của trung tuyến từ đỉnh C.
Kiến thức áp dụng
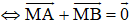
+ M là trung điểm của đoạn thẳng AB
+ M là trung điểm của đoạn thẳng thì với mọi điểm D ta có
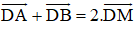
Bài 8 (trang 17 SGK Hình học 10): Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Lời giải:
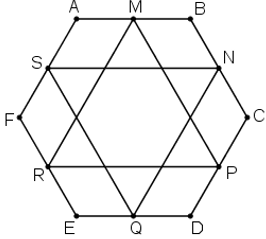
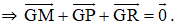
Gọi G là trọng tâm tam giác MPR

Ta cần đi chứng minh G cũng là trọng tâm của ΔNQS bằng cách chứng minh
Thật vậy ta có:
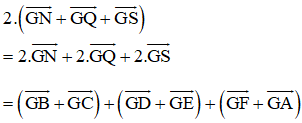
(Vì N, Q, S lần lượt là trung điểm của BC, DE, FA)
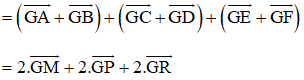
(Vì M, P, R là trung điểm AB, CD, EF)
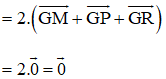
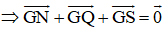
hay G cũng là trọng tâm của ΔNQS.
Vậy trọng tâm ΔMPR và ΔNQS trùng nhau.
Kiến thức áp dụng
G là trọng tâm ΔABC
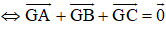
I là trung điểm đoạn thẳng AB
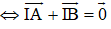
Bài 9 (trang 17 SGK Hình học 10): Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB.
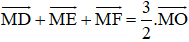
Chứng minh rằng
Lời giải:
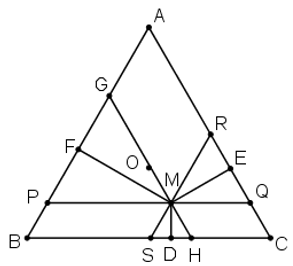
Ta có:
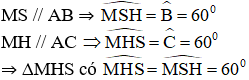
⇒ ΔMHS đều.
MD ⊥ SH nên MD là đường cao đồng thời là trung tuyến của ΔMHS.
⇒ D là trung điểm của HS
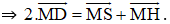
Chứng minh tương tự ta có:
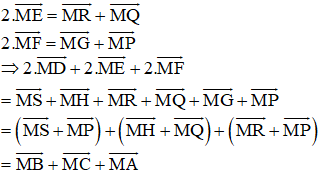
(Vì các tứ giác BSMP, HMQC, MRAG là hình bình hành)
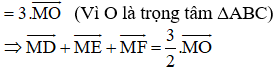
2twenty-seventh
arab friends gay webcam chat https://bjsgaychatroom.info/
free gay chat lines los angeles https://gaytgpost.com/
fcn gay chat https://gay-buddies.com/
gay dating for hung https://speedgaydate.com/
deep dish western slots https://2-free-slots.com/
wms free online slots https://candylandslotmachine.com/
river slots sweepstakes https://pennyslotmachines.org/
slots free single https://slotmachinesworld.com/
free play slots online https://slot-machine-sale.com/
sunset slots instant play https://beat-slot-machines.com/
2022 mlb draft bonus slots https://411slotmachine.com/
vegas world slots https://www-slotmachines.com/
gossip slots casino https://slotmachinegameinfo.com/
18-month doctorate without dissertation https://buydissertationhelp.com/
dissertation writing service https://help-with-dissertations.com/
masters dissertation writing https://mydissertationwritinghelp.com/
writing a rationale for dissertation https://dissertations-writing.org/
doctoral dissertation help your https://helpon-doctoral-dissertations.net/
Comments are closed.