
Câu hỏi 1 (trang 145 SGK Giải tích 12): Định nghĩa sự đơn điệu ( đồng biến, nghịch biến) của một hàm số trên một khoảng.
Lời giải:
Cho hàm số y = f(x) xác định trên K, hàm số f(x):
Đồng biến ( tăng) trên K nếu ∀ x1, x2 ∈ K: x1 < x2 => f(x1) < f(x2).
Nghịch biến ( giảm) trên K nếu ∀ x1, x2 ∈: x1 < x2 => f(x1) > f(x2)
Hàm số đồng biến hay nghịch biến trên K gọi là đơn điệu trên K.
Câu hỏi 2 (trang 145 SGK Giải tích 12): Phát biểu các điều kiện cần và đủ để hàm số f(x) đơn điệu trên một khoảng.
Lời giải:
Cho hàm số y = f(x) có đạo hàm trên K
Nếu f’(x) > 0, x ∈ K, f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số thì f(x) đồng biến trên K.
Nếu f’(x) < 0, x ∈ K, f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số f(x) nghịch biến trên K.
Câu hỏi 3 (trang 145 SGK Giải tích 12): Phát biểu các điều kiện đủ để hàm số f(x) có cực trị ( cực đại cực tiểu) tại điểm xo
Lời giải:
Điều kiện để hàm có cực trị:
Định lí 1: Cho hàm số y = f(x) liên tục trên K = (x0 – h; x0 + h), h > 0 và có đạo hàm trên K hoặc trên K \ {x0}, nếu:
– f’(x) > 0 trên (x0 – h; x0) và f’(x) < 0 trên (x0; x0 + h) thì x0 là một điểm cực đại của f(x).
– f’(x) < 0 trên (x0 – h; x0) và f’(x) > 0 trên (x0; x0 + h) thì x0 là một điểm cực tiểu của f(x).
Câu hỏi 4 (trang 145 SGK Giải tích 12): Nêu sơ đồ khảo sát sự biến thiên và vẽ đồ thị hàm số.
Lời giải:
Bước 1: Tìm tập xác định của hàm số
Bước 2: Xét sự biến thiên
– Xét chiều biến thiên:
+ Tìm đạo hàm f’(x)
+ Tìm các điểm mà tại đó f’(x) bằng không hoặc không xác định
+ Xét dấu của đạo hàm f’(x) và suy ra chiều biến thiên của hàm số.
– Tìm cực trị
– Tìm giới hạn vô cực và tiệm cận ( nếu có)
– Lập bảng biến thiên.
Bước 3: Vẽ đồ thị hàm số.
Câu hỏi 5 (trang 145 SGK Giải tích 12): Nêu định nghĩa và các tính chất cơ bản của loogarit.
Lời giải:

Câu hỏi 6 (trang 145 SGK Giải tích 12): Phát biểu định lí về quy tắc logarit, công thức đổi cơ số.
Lời giải:
• Quy tắc tính logarit
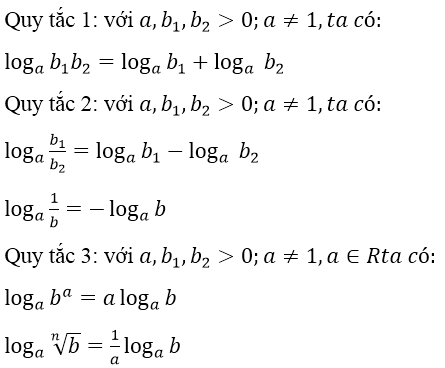
• Đổi cơ số

Câu hỏi 7 (trang 145 SGK Giải tích 12): Nêu tính chất của hàm số mũ, hàm số logarit, mối liên hệ giữa đồ thị của hàm số mũ cà hàm số logarit cùng cơ số.
Lời giải:
1. Hàm số mũ
Cho số a > 0, a ≠ 1. Hàm số y = ax được gọi là hàm số mũ cơ số a.
Khảo sát:
* D = R.
* Nếu:
– a > 1: hàm số luôn đồng biến
– 0 < a < 1: hàm số luôn nghịch biến
* Đồ thị luôn đi qua hai điểm ( 0; 1) và (1; a) có tiệm cận ngang là trục Ox.
2. Hàm Logarit
Cho số a > 0, a ≠ 1 . Hàm số
![]()
được gọi là hàm logarit cơ số a.
Khảo sát:
* D = (0;+∞)
* Nếu:
– a > 1: Hàm số luôn đồng biến trên D
– 0 < a < 1: hàm số luôn nghịch biến
* Đồ thị luôn đi qua hai điểm (1; 0) và (a; 1) có tiệm cận đứng là trục Oy.
• Liên hệ giữa đồ thị của hàm số mũ và hàm số logarit cùng cơ số: Đồ thị của hàm số mũ và đồ thị của hàm số logarit đối xứng nhau qua đường phân giác góc phần tư thứ nhất.
Câu hỏi 8 (trang 145 SGK Giải tích 12): Nêu định nghĩa và các phương pháp tính nguyên hàm.
Lời giải:
Nguyên hàm
Cho hàm số f(x) xác định trên K ( k là nửa khoảng hay đoạn của trục số). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K.
Phương pháp tính nguyên hàm
* Đổi biến số:

Câu hỏi 9 (trang 145 SGK Giải tích 12): Nêu định nghĩa và các phương pháp tính tích phân.
Lời giải:
• Định nghĩa
Cho hàm số y = f(x) liên tục trên [a; b] , F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x)
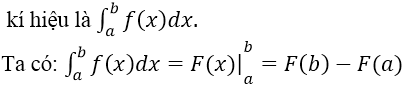
• Phương pháp tính tích phân
a) Đổi biến số:
Định lí 1: Cho hàm số f(x) liên tục trên [a; b]. Giả sử hàm số x = φ(t) có đạo hàm liên tục trên đoạn [ α;β] sao cho φ(α) = a; φ(β) = βvà a ≤ φ(t) ≤ b với mọi t ∈ [α;β]. Khi đó:
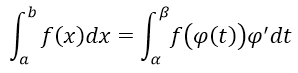
b) Tích phân từng phần
Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì:
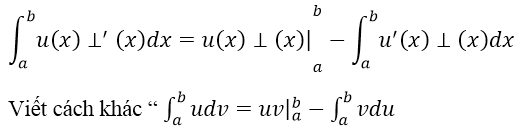
Câu hỏi 10 (trang 145 SGK Giải tích 12): Nhắc lại định nghĩa số phức, số phức liên hợp, mô đun của số phức. Biểu diễn hình học của số phức.
Lời giải:
1. Số phức
Mỗi biểu thức dạng a + bi, trong đó: a, b ∈ R;i2= -1 được gọi là số phức. Trong đó a được gọi là phần thực, b gọi là phần ảo, số i là đơn vị ảo.
2. Mô đun
Cho số phức z = a + bi, được biểu diễn bởi điểm M(a;b) trên tọa độ Oxy. Ta gọi mô đun của số phức z, kí hiệu là |z| là đọ dài của vectơ OM.
![]()
3. Số phức liên hợp
Cho số phức z = a + bi, ta gọi a – bi là số phức liên hợp của z
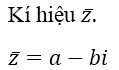
Bài 1 (trang 145 SGK Giải tích 12): Cho hàm số f(x)=ax2-2(a+1)x+a+2 (a ≠ 0)
a) Chứng tỏ rằng phương trình f(x)=0 luôn có nghiệm thực. Tính các nghiệm đó.
b) Tính tổng S và tích P của các nghiệm của phương trình f(x) =0. Khảo sát sự biến thiên và vẽ đồ thị của S và P theo a.
Lời giải:

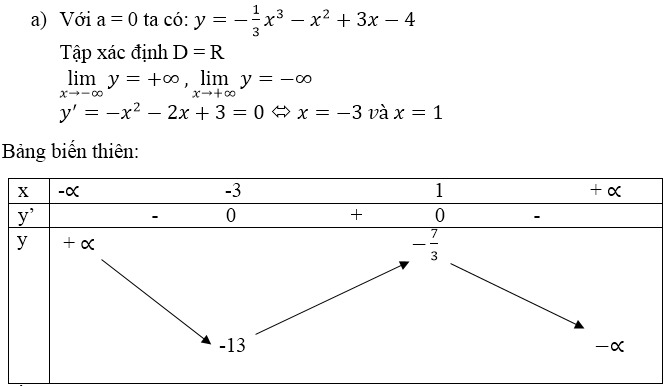
Bảng biến thiên:

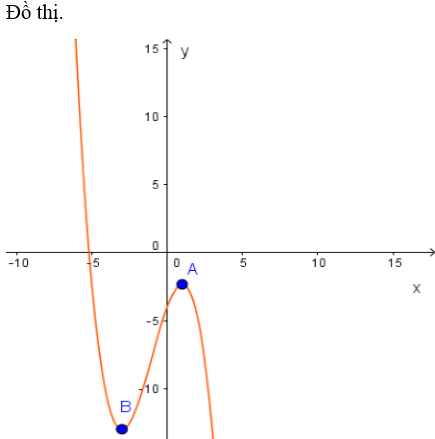
Đồ thị (hình thang trên).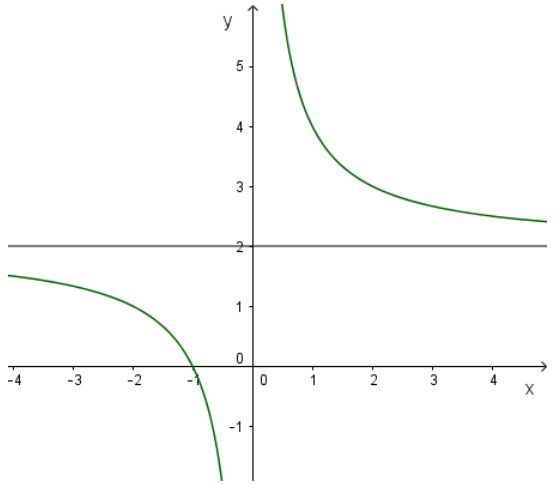
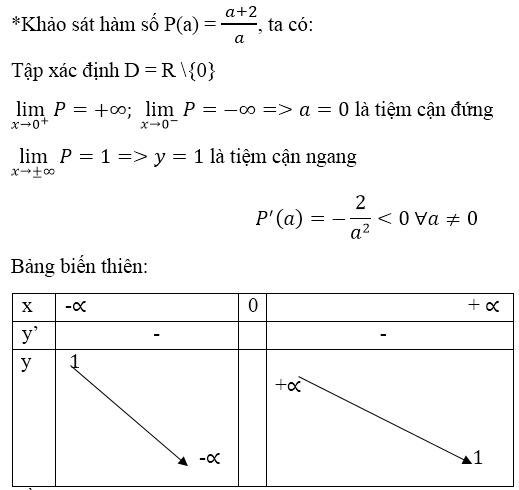
Đồ thị ( hình trên).
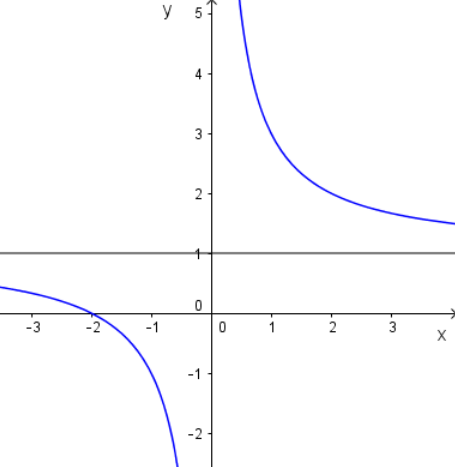
Bài 2 (trang 145 SGK Giải tích 12): Cho hàm số

Lời giải:

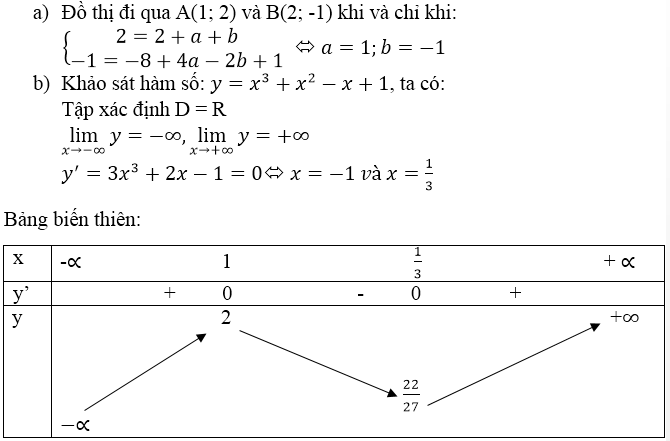
Bài 3 (trang 146 SGK Giải tích 12): Cho hàm số y = x3 + ax2 + bx+1
a) Tìm a và b để đồ thị của hàm số đi qua hai điểm: A(1;2)và B(-2;-1).
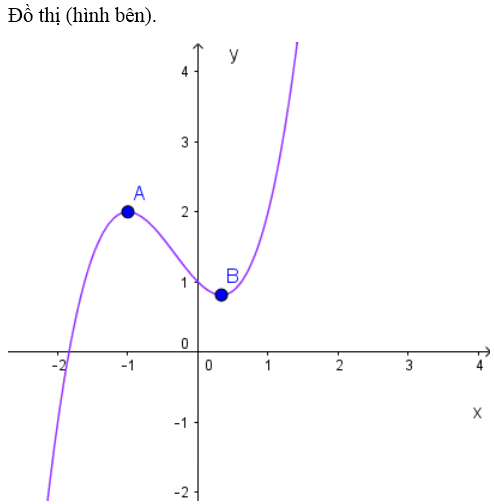
b) Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số ứng với các giá trị tìm được của a và b.
c) Tính thể tích vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường y = 0, x = 0, x = 1 và đồ thị (C ) xung quanh trục hoành.
Lời giải:
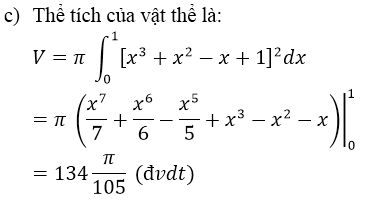
Bài 4 (trang 146 SGK Giải tích 12): Xét chuyển động thẳng được xác định bởi phương trình:
Trong đó t được tính bằng giây và S được tính bằng mét.
a) Tính v(2), a(2), biết v(t), a(t) lần lượt là vận tốc và gia tốc chuyển động đã cho.
b) Tìm thời điểm t mà tại đó vận tốc bằng 0.
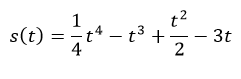
Lời giải:
Theo ý nghĩa cơ học của đạo hàm ta có:
v(t)=s‘(t)=t3-3t2+t-3
v(2)=23-3.22+2-3=-5 (m/s)
a(t)=v‘(t)=s”(t)=3t2-6t+1
a(2)=3.22-6.2+1=1 (m/s2)
v(t)=t3-3t2+t-3=0
(t-3)(t1+1)=0 => t = 3
Vậy thời điểm to=3s thì vận tốc bằng 0.
Bài 5 (trang 146 SGK Giải tích 12): Cho hàm số y = x4 + a4 + b
a) Tính a, b để hàm số cực trị bằng 3/2 khi x =1.
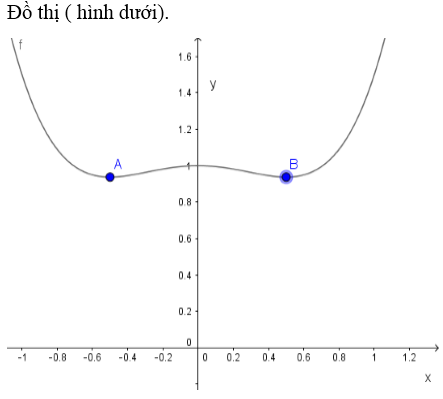
b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho khi:
a=-1/2,b=1
c) Viết phương trình tiếp tuyến của (C) tại các điểm có tung độ bằng 1.
Lời giải:
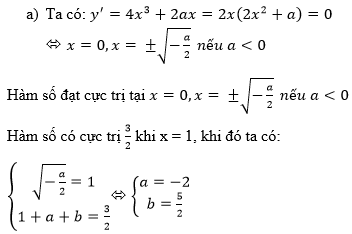
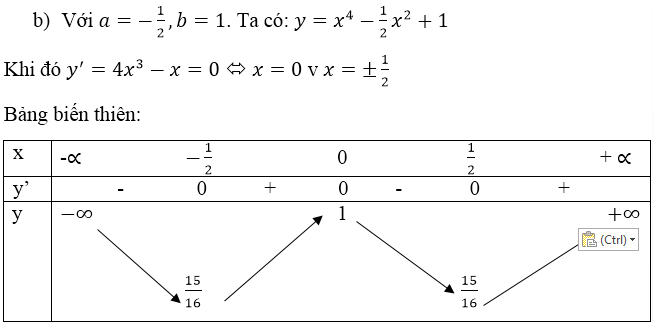
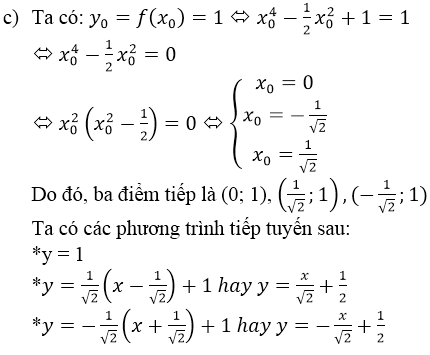
Bài 6 (trang 146 SGK Giải tích 12):
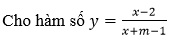
b) Viết phương trình tiếp tuyến d của đồ thi (C ) tại điểm M có hoành độ a ≠ -1.
Lời giải:
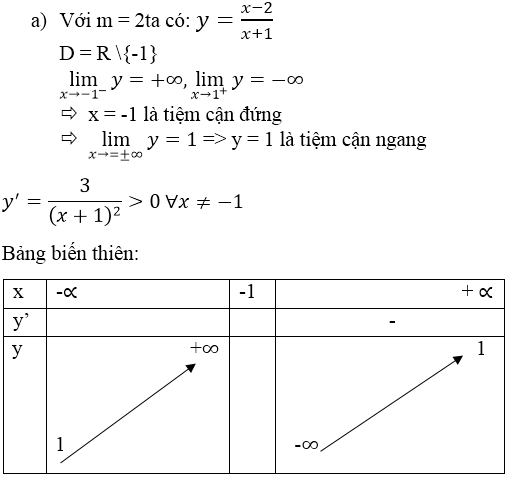
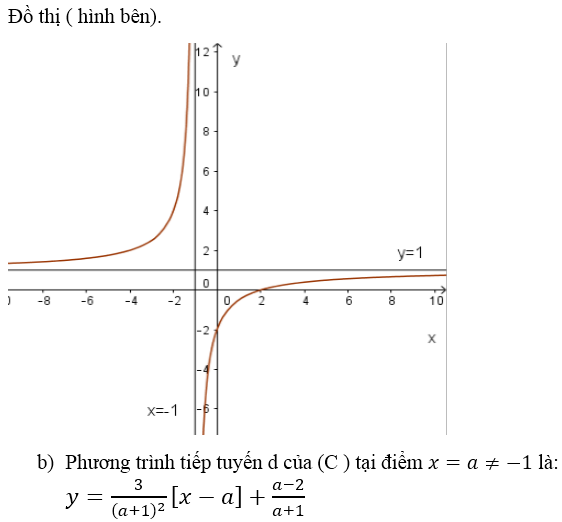
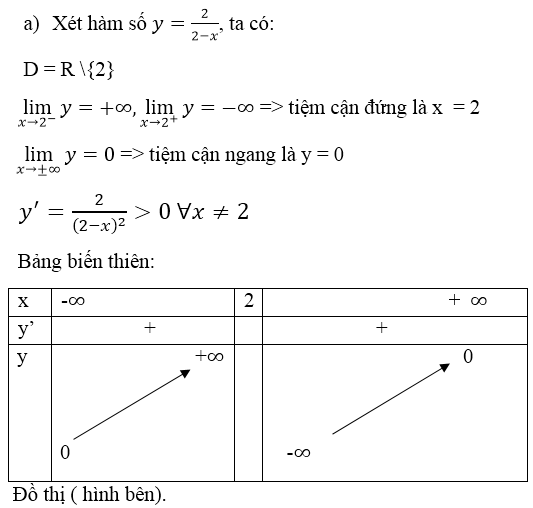
Bài 7 (trang 146 SGK Giải tích 12): Cho hàm số
![]()
a) Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số đã cho.
b) Tìm giao điểm của (C ) và đồ thị hàm số y=x2+1 . Viết phương trình tiếp tuyến của (C ) tại mỗi giao điểm.
c) Tính thể tích vật tròn xoay thu được khi hình phẳng H giới hạn bởi đồ thị (C ) và các đường thẳng y = 0; x = 1 xung quanh trục Ox.
Lời giải:

Bài 8 (trang 147 SGK Giải tích 12): Tìm giá trị lớn nhất và nhỏ nhất của hàm số:
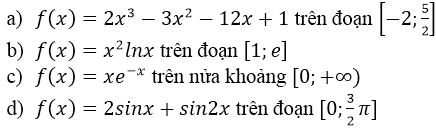
Lời giải
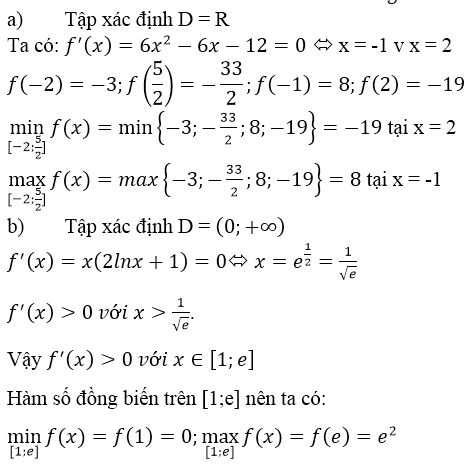
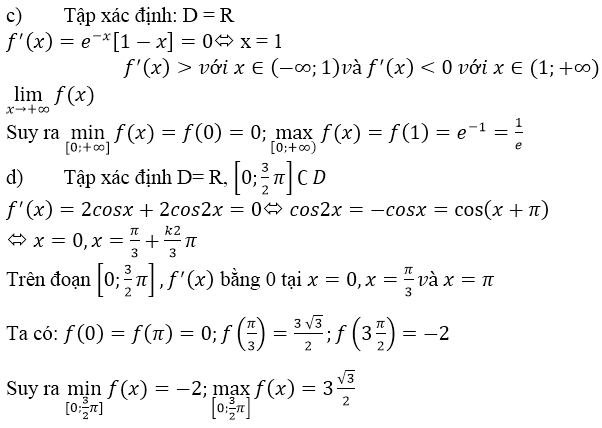
Bài 9 (trang 147 SGK Giải tích 12): Giải các phương trình sau:
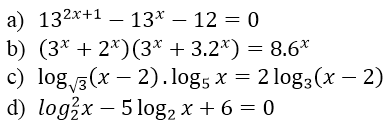
Lời giải
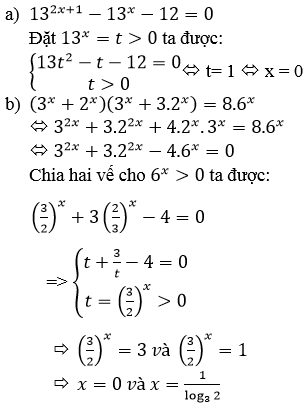
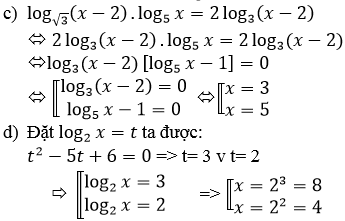
Bài 10 (trang 147 SGK Giải tích 12): Giải các bất phương trình sau:
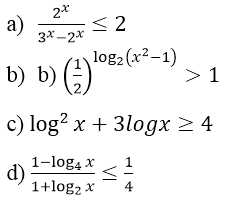
Lời giải


Bài 11 (trang 147 SGK Giải tích 12): Tính các tích phân sau bằng phương pháp tích phân từng phần:
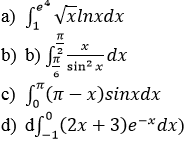
Lời giải
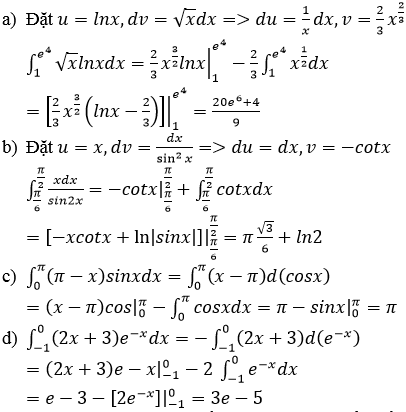
Bài 12 (trang 147 SGK Giải tích 12): Tính các tích phân sau bằng phương pháp đổi biến số:
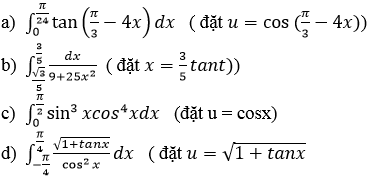
Lời giải
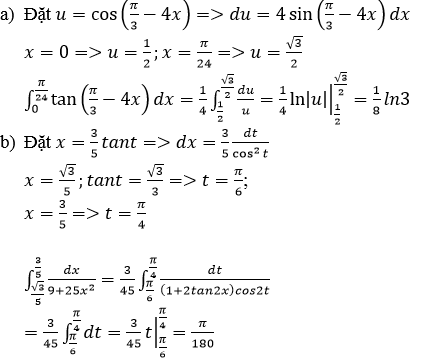
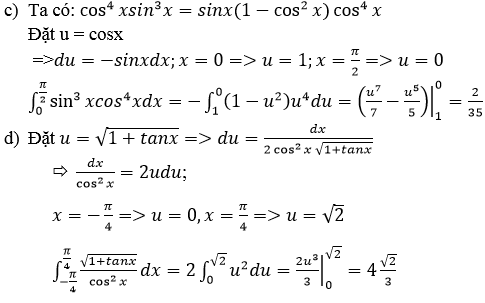
Bài 13 (trang 148 SGK Giải tích 12): Tính diện tích hình phẳng giới hạn bởi các đường:
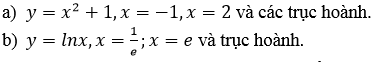
Lời giải
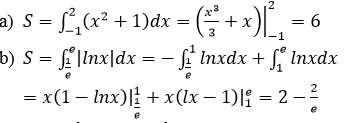
Bài 14 (trang 148 SGK Giải tích 12): Tìm thể tích vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường y = 2x2 và y = x3 xung quanh trục Ox.
Lời giải:
Ta có: 2x2 = x3 ⇔ x2 (2 – x) = 0 ⇔ x = 0 và x = 2
Hoành độ giao điểm của hai đường cong là: x = 0 và x =2
Bởi vì 2x2=x3=x2 (2-x)≥0 với x≤2 nên đường cong y=2x2 nằm trên đường cong y=x3 trong khoảng (0; 2). Do đó thể tích cần tính là:
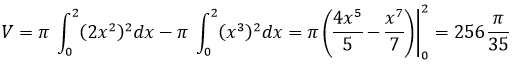
Bài 15 (trang 148 SGK Giải tích 12): Giải các phương trình sau trên tập số phức:
(3+2i)z-(4+7i)=2-5i
(7-3i)z+(2+3i)=(5-4i)z
z2-2z+13=0
z4-z2-6=0
Lời giải
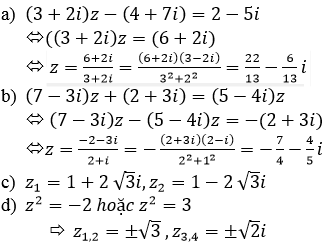
Bài 16 (trang 148 SGK Giải tích 12): Trên mặt phẳng tọa độ, hãy tìm tập hợp các điểm biểu diễn số phức z thỏa mãn từng bất đẳng thức:
a) |z| < 2
b) |z – i| ≤ 1
c) |z – 1 – i| < 1
Lời giải:
a) Tập hợp các điểm M(x; y) của mặt phẳng tọa độ biểu diễn số phức z = x + yi thỏa mãn điều kiện:
|z|<2 ⇔ √(x2+y2 )<2 ⇔x2+y2<4
Các điểm M(x; y) như vậy nằm trong đường tròn có tâm O bán kính bằng 2 không kể các điểm trên đường tròn.
b) Giả sử z=x+yi=>z-i=z+(y-1)i
|z-1|≤1 ⇔ √(x2 (y-1)2 )≤1 ⇔x2+(y-1)2≤1
Tập hợp tất cả các điểm biểu diễn các số phức thỏa mãn |z – 1|≤1 là các điểm của hình tròn tâm (0; 1) bán kính bằng 1 kể cả biên.
c) z=x+yi=>z-1-i=(x-1)+(y-1)i
|z-1-i|<1 ⇔ (x-1)2+(y-1)2<1
Tập hợp các điểm đang xét là các điểm của hình tròn ( không kể biên) tâm (1;1), bán kính bằng 1.