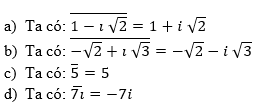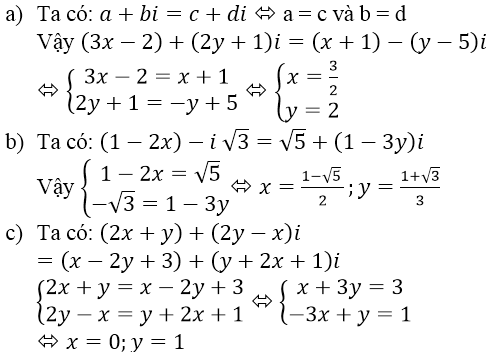
Bài 1 (trang 133 SGK Giải tích 12): Tính phần thực phần ảo của số phức x, biết:
a) z=1-πi
b) z=√2-i
c) z=2 √2
d) z=-7i
Lời giải:
a) Phần thực: 1, phần ảo: -π
b) Phần thực: √2, phần ảo: -1
c) Phần thực: 2 √2, phần ảo: 0
d) Phần thực: 0, phần ảo: -7
Bài 2 (trang 133 SGK Giải tích 12): Tìm các số thực x và y, biết:
a) (3x-2)+(2y+1)i=(x+1)-(y-5)i
b) (1-2x)-i √3=√5+(1-3y)i
c) (2x+y)+(2y-x)i=(x-2y+3)+(y+2x+1)i
Lời giải:
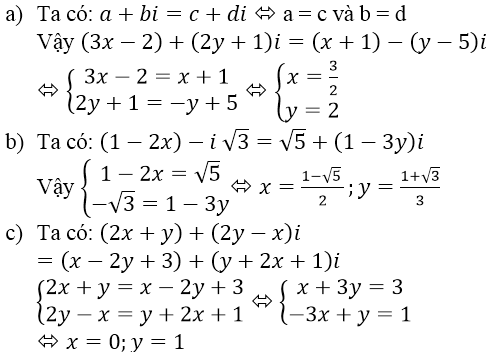
Bài 3 (trang 133 SGK Giải tích 12): Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:
a) Phần thực của z bẳng -2
b) Phần ảo của z bẳng 3
c) Phần thực của z thuộc khoảng (-1;2)
d) Phần ảo của z thuộc đoạn [1;3]
e) Phần thực và phần ảo đều thuộc đoạn [-2; 2]
Lời giải:
a) Tập hợp các điểm thuộc đường thẳng x = -2
b) Tập hợp các điểm thuộc đường thẳng y = 3
c) Tập hợp các điểm thuộc mặt phẳng nằm giữa hai đường thẳng song song x = -1 và x =2 (hình có gạch sọc)
d) Phần mặt phẳng giới hạn bởi các đường thẳng song song y =1 và y = 3( kể cả các điểm thuộc hai đường thẳng đó).
e) Các điểm thuộc hình chữ nhật với các cạnh nằm trên các đường thằng x = -2, x = 2 , y= -2, y= 2.
Bài 4 (trang 134 SGK Giải tích 12): Tính |z|, với:
a) z = -2 + i √3
b) z = √2- 3i
c) z = -5
d) z = i√3
Lời giải:
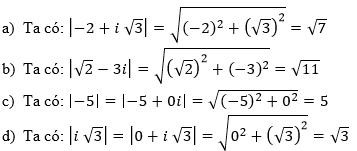
Bài 5 (trang 134 SGK Giải tích 12): Trên mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn từng điều kiện:
a) |z| = 1
b) |z| ≤ 1
c) 1<|z| ≤ 2
d) |z| = 1 và phần ảo của z = 1
Lời giải:
a) Giả sử điểm M(x, y) biểu diễn số phức z=x+y thỏa mãn:
|z|=|x+yi|=1 ⇔√(x2+y2 )=1
⇔x2+y2=1
Vậy M thuộc đường tròn tâm O(0; 0) bán kính R =1 có phương trình x2+y2=1.
b) Tập hợp các điểm trên hình tròn tâm x2+y2=1.
c) Các điểm nằm trong hình vành khăn giới hạn bởi các đường tròn tâm O, bán kính tròn nhở bằng 1,đường tròn lớn bằng 2, (hình tô đậm) không kể các điểm thuộc đường tròn nhỏ.
d) Giao điểm của đường thẳng y = 1 và đường tròn x2+y2=1.
Bài 6 (trang 134 SGK Giải tích 12): Tìm z, biết:
a) z=1-i √2
b) z=-√2+i √3
c) z=5
d) z=7i
Lời giải: