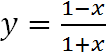
Bài 1 (trang 47 SGK Giải tích 12): Số điểm cực trị của hàm số y = – 1/3 x3 – x + 7 là:
(A) 1 ; (B) 0 ; (C) 3 ; (D) 2
Lời giải:
– Chọn đáp án B
– Ta có: y’ = -x2 – 1 < 0 ∀ x ∈ R
Hàm số luôn nghịch biến trên tập xác định nên không có cực trị.
Bài 2 (trang 47 SGK Giải tích 12): Số điểm cực đại của hàm số y = x4 + 100 là:
(A) 0 ; (B) 1 ; (C) 2 ; (D) 3
Lời giải:
– Chọn đáp án A
– Ta có: y’ = 4x3 = 0 ⇔ x = 0
Hàm số nghịch biến trên (-∞; 0) và đồng biến trên (0; +∞) => hàm số chỉ có cực tiểu chứ không có cực đại.
(Bạn có thể vẽ bảng biến thiên để thấy rõ hơn.)
Bài 3 (trang 47 SGK Giải tích 12): Số đường tiệm cận của đồ thị hàm số
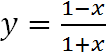
là: (A) 1 ; (B) 2 ; (C) 3 ; (D) 0
Lời giải:
– Chọn đáp án B
– Ta có: 1 + x =0 ⇔ x = -1
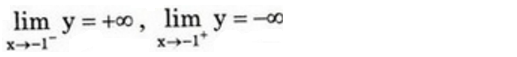
Đồ thị hàm số có tiệm cận đứng x = -1.
![]()
Đồ thị hàm số có tiệm cận ngang y = -1.
=> Đồ thị hàm số có 2 đường tiệm cận.
Bài 4 (trang 47 SGK Giải tích 12): Hàm số
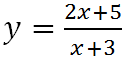
đồng biến trên: (A) R ; (B) (-∞;3) ; (C) (-3; +∞) ; (D) R \ {-3}
Lời giải:
– Chọn đáp án D
– TXĐ: D = R \ {-3}
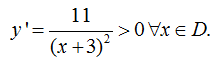
=> Hàm số đồng biến trên D = R \ {-3}.
Bài 5 (trang 47 SGK Giải tích 12): Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số:
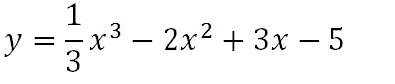
(A) Song song với đường thẳng x = 1;
(B) Song song với trục hoành;
(C) Có hệ số góc dương;
(D) Có hệ số gọc bằng -1.
Lời giải:
– Chọn đáp án B
– Ta có: y’ = x2 – 4x + 3
y’ = 0 ⇔ x = 1 ; x = 3
y”= 2x – 4
Ta có: y”(3) = 2 > 0
=> hàm số đạt cực tiểu tại x = 3 (Quy tắc 2).
Mặt khác, phương trình tiếp tuyến tại điểm cực tiểu có hệ số góc là y'(3) = 0. Do đó tiếp tuyến song song với trục hoành.