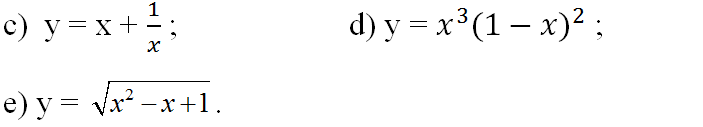
Bài 1 (trang 18 SGK Giải tích 12): Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
a) y = 2x3 + 3x2 – 36x – 10 ; b) y = x4 + 2x2 – 3;
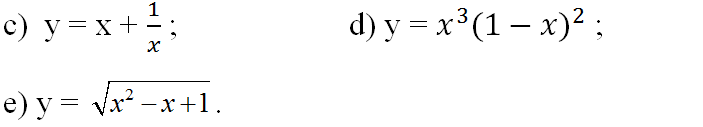
Lời giải
a) TXĐ: D = R
y’ = 6x2 + 6x – 36 = 6(x2 + x – 6)
y’ = 0 => x = -3 hoặc x = 2
Bảng biến thiên:
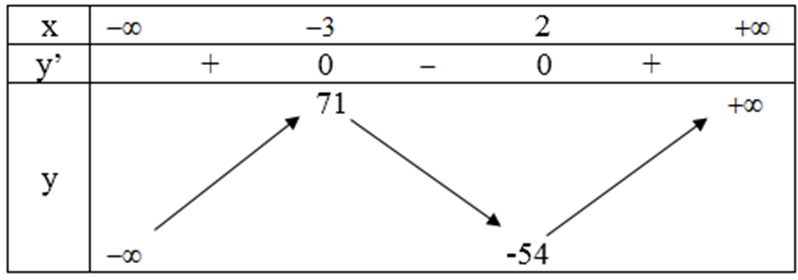
Vậy đồ thị của hàm số có điểm cực đại là (-3; 71) và điểm cực tiểu là (2; -54).
b) TXĐ: D = R
y’= 4x3 + 4x = 4x(x2 + 1) = 0; y’ = 0 => x = 0
Bảng biến thiên:
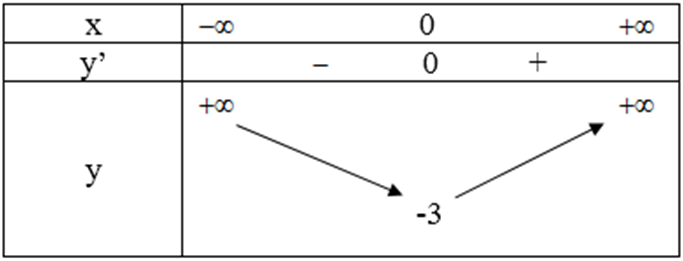
Vậy hàm số có điểm cực tiểu là (0; -3).
c) TXĐ: D = R \ {0}
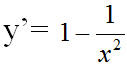
y’ = 0 => x = ±1
Bảng biến thiên:
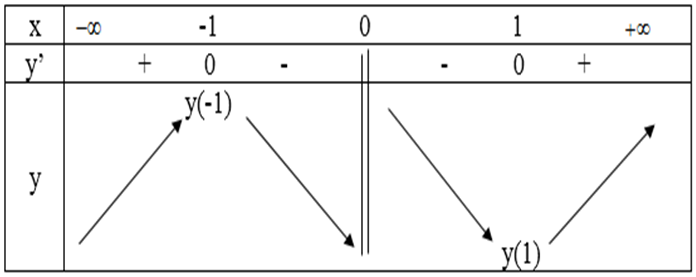
Vậy hàm số có điểm cực đại là xCĐ = -1 và điểm cực tiểu là xCT = 1.
d) TXĐ: D = R
y’= 3x2(1 – x)2 – 2x3(1 – x) = x2(5x2 – 8x + 3)
y’ = 0 => x = 0; x = 1 hoặc x = 3/5
Bảng biến thiên:
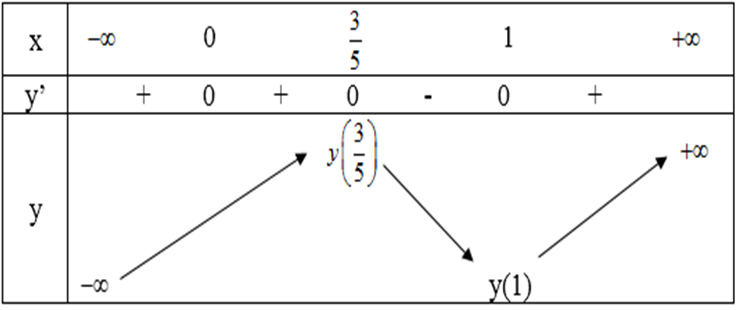
Vậy hàm số cực đại xCĐ = 3/5 và điểm cực tiểu xCT = 1
(Lưu ý: x= 0 không phải là cực trị vì tại điểm đó đạo hàm bằng 0 nhưng đạo hàm không đổi dấu khi đi qua x = 0.)
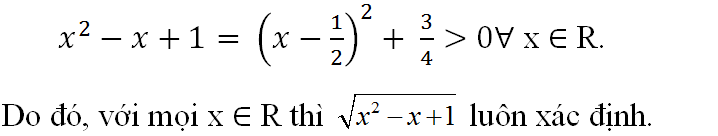
Vậy D = R.
Bảng biến thiên:

Vậy hàm số có điểm cực tiểu xCT = 1/2.
Bài 2 (trang 18 SGK Giải tích 12): Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau:
a) y = x4 – 2x2 + 1 ; b) y = sin2x – x
c) y = sinx + cosx ; d) y = x5 – x3 – 2x + 1
Lời giải:
a) TXĐ: D = R.
y’ = 4x3 – 4x
y’= 0 => x = 0; x = ±1.
y” = 12x2 – 4
y”(0) = -1 < 0 => x = 0 là điểm cực đại của hàm số.
y”(±1) = 8 > 0 > x = -1 và x = 1 là điểm cực tiểu của hàm số.
b) TXĐ: D = R
y’ = 2cos2x – 1;

c) TXĐ: D = R
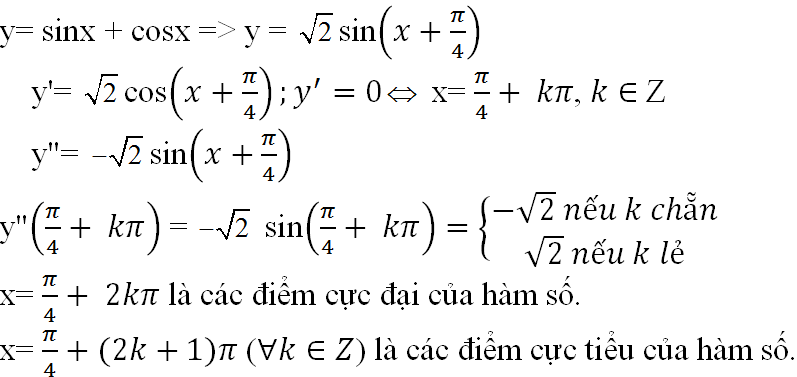
d) TXĐ: D = R
y’= 5x4 – 3x2 – 2
y’ = 0 => x ±1.
y” = 20x3 – 6x
y”(-1) = -20 + 6 = -14 < 0 => x = -1 là điểm cực đại của hàm số.
y”(1) = 20 – 6 = 14 > 0 => x = 1 là điểm cực tiểu của hàm số.
Bài 3 (trang 18 SGK Giải tích 12): Chứng minh hàm số y = √|x| không có đạo hàm tại x = 0 nhưng vẫn đạt được cực tiểu tại điểm đó.
Lời giải:
Tính theo định nghĩa đạo hàm tại xo = 0 ta có:
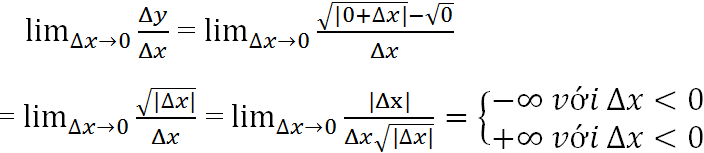
Nghĩa là hàm số y = √|x| không có đạo hàm tại x = 0. (1)
Mặt khác ta có: √|x| ≥ 0 ∀ x. Dấu “=” xảy ra khi x = 0.
Do đó hàm số y = √|x| đạt cực tiểu tại x = 0. (2)
Từ (1) và (2) suy ra điều phải chứng minh.
Bài 4 (trang 18 SGK Giải tích 12): Chứng minh rằng với mọi giá trị của tham số m, hàm số
y = x3 – mx2 – 2x + 1
luôn luôn có một cực đại và một điểm cực tiểu.
Lời giải:
Xét hàm số y = x3 – mx2 – 2x + 1 ta có:
TXĐ: D = R
y’ = 3x2 – 2mx – 2
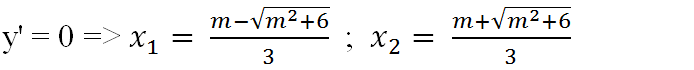
Với mọi giá trị của m ta đều có x1 < 0 < x2.
Bảng biến thiên:
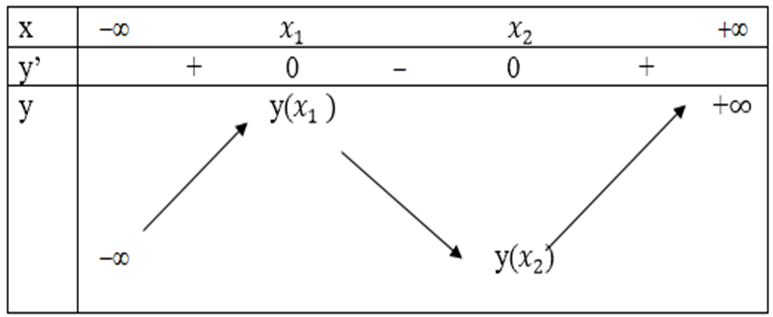
Từ bảng trên ta thấy hàm số luôn có một điểm cực đại xCĐ = x1 và một điểm cực tiểu xCT = x2 với mọi giá trị của m (đpcm).
Bài 5 (trang 18 SGK Giải tích 12): Tìm a và b để các cực trị của hàm số
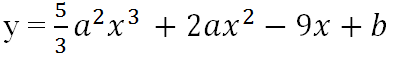
đều là nhưng số dương và xo = -5/9 là điểm cực đại.
Lời giải:
– Nếu a = 0 thì y = –9x + b. Vậy hàm số không có cực trị.
– Nếu a ≠ 0. Ta có: y’= 5a2x2 + 2ax – 9
y’= 0 => x = 1/a hoặc x = -9/5a
+ Với a > 0 ta có bảng biến thiên:
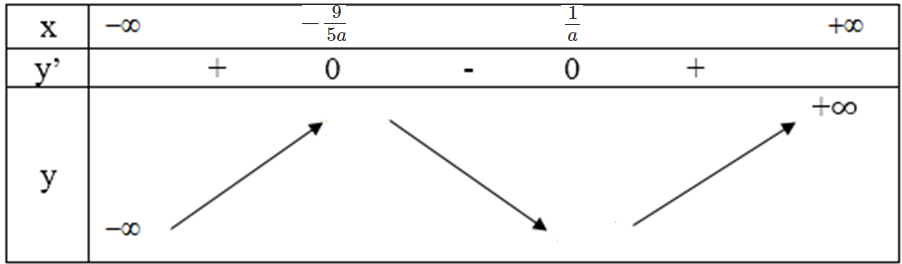
Vì xo = -5/9 là điểm cực đại nên
![]()
Theo đề bài thì yCT dương nên với a = 81/25 thì khi đó:
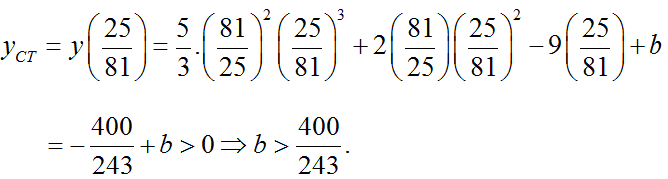
+ Với a < 0 ta có bảng biến thiên:
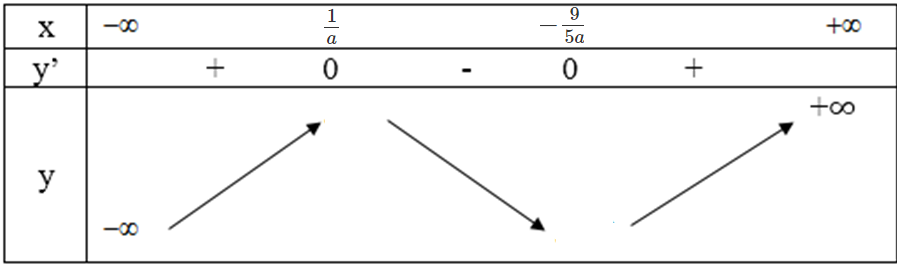
Vì xo = -5/9 là điểm cực đại nên
![]()
Theo đề bài thì yCT dương nên với a = -9/5 thì khi đó:
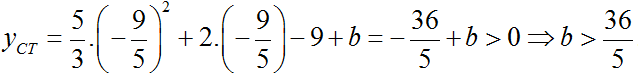
Vậy các giá trị a, b cần tìm là:
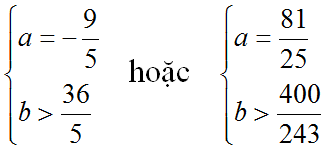
Bài 6 (trang 18 SGK Giải tích 12): Xác định giá trị của tham số m để hàm số m để hàm số
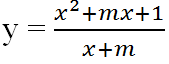
đạt giá trị cực đại tại x = 2.
Lời giải:
TXĐ: D = R \ {-m}
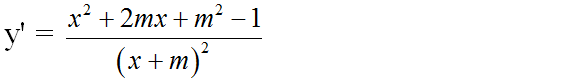
y’ = 0 => x1 = -m – 1; x2 = -m + 1
Bảng biến thiên:
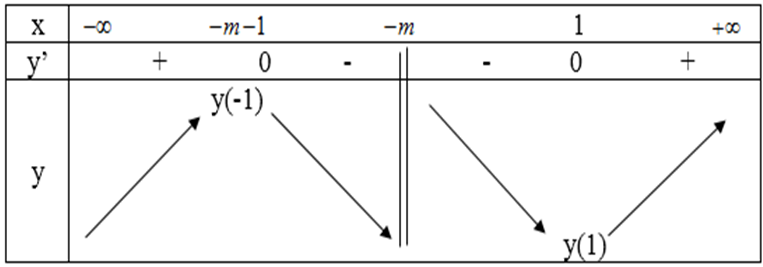
Hàm số đạt cực đại tại x = 2 ⇔ – m – 1 = 2 => m = –3.
[…] trị hàm số Hàm số – 5. Cực trị hàm số kkhtn.duytan.edu.vn kkhtn.duytan.edu.vn lop12.edu.vn Giải tích – Chương 1 – Bài 2: Cực trị của hàm số Bài 1 (trang 18 SGK Giải tích […]
[…] cực đại và cực tiểu tại các điểm có hoành độ dương. Em cảm ơn ạ!! lop12.edu.vn Giải tích – Chương 1 – Bài 2: Cực trị của hàm số Bài 1 (trang 18 SGK Giải tích […]
[…] nhất, giá trị nhỏ nhất của hàm số đó. Lấy một ví dụ như sau: Trong … lop12.edu.vn Giải tích – Chương 1 – Bài 2: Cực trị của hàm số Bài 1 (trang 18 SGK Giải tích […]
Comments are closed.