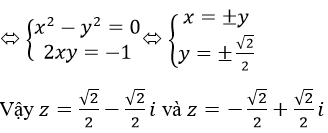
Bài 17 (trang 195 sgk Giải Tích 12 nâng cao):
Tìm các căn bậc hai của số phức sau: -i; 4i; -4;1+4 √3 i
Lời giải:
Gọi z=x+yi là căn bậc hai của -I, ta có: z2=-i
<=> (x+yi)2=-i <=> x2-y2+2xyi=-i
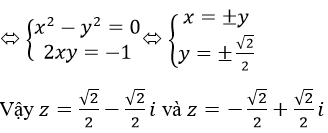
Tương tự, 4i có căn bậc hai là z=√2+√2 i và z=-√2-√2 i; -4 có căn bậc hai là: z = 2i và z = -2i, 1+4 √3 i và z=-2-2 √3 i
Bài 18 (trang 196 sgk Giải Tích 12 nâng cao):
Chứng minh rằng nếu z là căn bậc hai của số phức w thì |z| = √(|w| )
Lời giải:
Giả sử w=a+bi có một căn bậc hai là z=x+yi
Vì z là một căn bậc hai của w nên z2=w
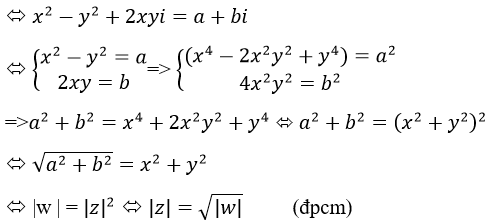
Bài 19 (trang 196 sgk Giải Tích 12 nâng cao):
Giải các phương trình bậc hai sau:
a) z2=z+1 b) z2+2z+5=0 c) z2+(1-3i)z-2(1+i)=0
Lời giải:
a) z2=z+1 <=> z2-z-1=0, có Δ=5
![]()
Vậy phương trình có hai nghiệm là
![]()
b) z2+2z+5=0,có Δ=-16=16i2=(4i)2
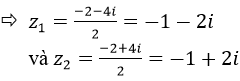
Vậy Phương trình có hai nghiệm là: z1=-1-2i;z2=-1+2i
c) z2+(1-3i)z-2(1+i)=0
Ta có Δ=(1-3i)2+8(1+i)=2i
Δ có căn bậc hai là: a1=1+i,a2=-1-i
Nên Phương trình có 2 nghiệm là:
z1=2i;z2=-1+i
Bài 20 (trang 196 sgk Giải Tích 12 nâng cao):
a) Hỏi công thức Viet về Phương trình bậc hai với hệ số thực có còn đúng cho Phương trình bậc hai với hệ số phức không? Vì sao?
b) Tìm hai số phức, biế tổng của chúng bằng 4 – I và tích của chúng bằng 5(1 – i).
c) Có phải mọi phương trình bậc hai z2+Bx+C=0 (B, C là hai số phức nhận hai nghiệm là hai số phức liên hợp không thực phải có các hệ số B, C là hai số thực? vì sao? Điều ngược lại có đúng không?
Lời giải:
a) Định lí Viet vẫn đúng cho Phương trình bậc hai với hệ số phức,
Giả sử Phương trình: Az2+Bz+C=0 (A ≠ 0;A,B,C ∈C) có hai nghiệm:
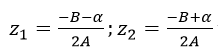
với α là một căn bậc hai của biệt số Δ=B2-4AC
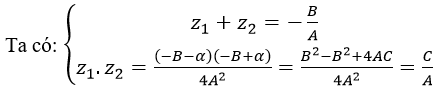
b) Theo định lí Viet thì hai số phức có nghiệm của Phương trình:
z2-(4-i)z+5(1-i)=0 (*)
Ta có Δ=(4-i)2-20(1-i)=-5+12i
Δ là một căn bậc hai là α=2+3i, nên (*) có hai nghiệm là:
![]()
Vậy hai số cần tìm là: 3+i;1-2i
c) Giả sử phương trình: z2+Bz+C=0 nhận hai nghiệm là hai số phức liên hợp không thức sau đây: z1=a+bi;z2=a-bi với b ≠ 0;a.b ∈R
Vì z1;z2 là nghiệm Phương trình: z2+Bz+C=0 nên ta có:
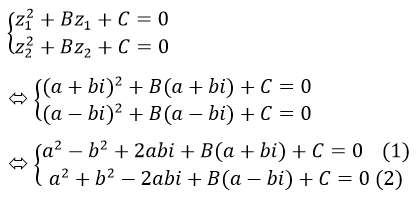
Cộng vế với vế của (1) và (2) ta được:
2a2+2aB+2C=0 <=> a2+aB+C=0 => c=-(a2+aB)
Thay vào (1) ta được:
(1) <=> a2-b2+2abi+B(a+bi)-(a2+aB)=0
<=> -b2+2abi+bBi=0 (vì b ≠ 0)
![]()
Vì b ≠ 0 nên B = -2a – bi không thể là một số thực, vật khẳng định: B và C là hai số thực là sai.
– Điều ngược lại. nếu B, C là hai số thực thì Phương trình z2+Bz+C=0 nhận hai nghiệm số phức liên hợp là sai, chẳng hạn Phương trình z2+2z-3=0 có nghiệm là z = 1; z =-3
Bài 21 (trang 197 sgk Giải Tích 12 nâg cao):
a) Giải Phương trình: (z2+i)(z2-2iz-1)=0
b) Tìm số phức B để Phương trình bậc hai z2 Bz+3i=0 có tổng bình Phương hai nghiệm bằng 8.
Lời giải:
a) Phương trình: (z2+i)(z2-2iz-1)=0
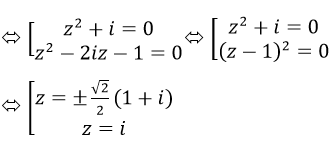
Vậy Phương trình đã cho có 3 nghiệm:
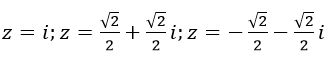
b) Theo bài ra ta có: z12+z22=8 <=> (z1+z2 )2-2z1 z2=8
<=> B2-6i=8 (vì theo Viet z1+z2=-B;z1 z2=3i
<=> B2=6i+8, vậy B là căn bậc hai của 6i + 8
Số 6i + 8 có căn bậc hai là: 3+i và-3-i
Vậy B = 3 + i hoặc B = -3 – i
Đáp số: có hai số B thỏa mãn bài toán.
Bài 22 (trang 197 sgk Giải Tích 12 nâng cao)
Đố vui. Một học sinh kí hiệu một căn bậc hai của -1 là √(-1) và tính √(-1).√(-1) như sau:
a) Tính theo định nghĩa của căn bậc hai là -1 thì √(-1).√(-1)=-1
b) Tính theo tính chất của căn bậc hai (tích của hai căn bậc hai của hai số bằng căn bậc hai của tích hai số đó) thì:
√(-1).√(-1)=√((-1)(-1) )=√1=1
Từ đó, học sinh suy ra – 1 = 1. Hãy tìm điều sai trong lập luận trên.
Lời giải:
1. Trước hết không nên kí hiệu √(-1) là một căn bậc hai của -1, bởi vì trong phần lí thuyết ta đã biết số -1 có dùng căn bậc hai là: √(-(-1) ) i và -√(-(-1) ) i. Kí hiệu √a chỉ nên chỉ: “Giá trị không âm của căn bậc hai của số thực không âm a” mà thôi.
2. Sai lầm chính ở điểm b). học sinh đó đã xem kí hiệu mới của mình √(-1) như là căn bậc hai số học của một số thực không âm, mặc dù rằng √(-1) không phải là một số thực. (học sinh đó dùng √(-1) để chỉ số ảo i hoặc số ảo -i) và kí hiệu mới √(-1) của học sinh đó cũng không có tính chất tương tự như tính chất của √a (Với a là số thực không âm) mà bằng chứng là chính mâu thuẫn tìm được trong b)
3. Một sai lầm nữa phải nhắc đến đó là: tính chất trong b) “tích của hai căn bậc hai của hai số bằng căn bậc hai của hai số đó” là phát biểu sai, chẳng hạn.
Ví dụ: số 2 là một căn bậc hai của 4.
Số -3 là một căn bậc hai của số 9
Số 6 là một căn bậc hai của số 4.9
Theo tính chất trên thì:2(-3) = 6, đường nhiên sai.
Ví dụ 2. Số I là một căn bậc hai của số -1;
Số I +1 là một căn bậc hai của 2i
Số I – 1 là một căn bậc hai của số -1.2i
Theo tính chất trên thì:
i(i+1)=1-i <=> -1+i=1-i. Sai bản chất của sai lầm của biến đổi trong b) không phải sai do sai trong 3) mà do sai trong 2). Nhưng sai lầm trong 3) cũng cần trách.
4. Cần giải thích thêm sự phân tích trong 2) như sau:
Tính chất. nếu x, y là các số thực không âm thì: √x √y=√(x.y) (1)
Khi kí hiệu: √(-1).√(-1)=√((-1)(-1) )=1, nghĩa là đã xem số -1 thõa mãn tích chất -1 ≥ 0
Con đường dẫn đến sai lầm của học sinh đó (có lẽ) diễn ta như sự phân tích trong 4).