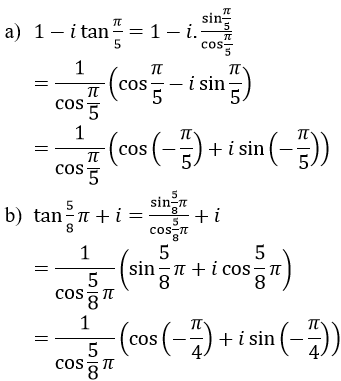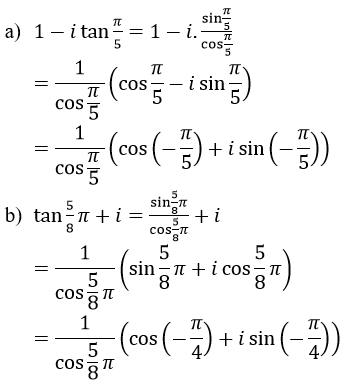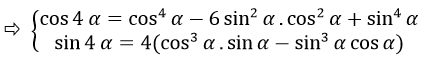
Bài 32 (trang 207 sgk Giải Tích 12 nâng cao):
Sử dụng công thức Moa-vrơ để tính sin4α và cos4α theo các lũy thừa sinα và cosα
Lời giải:
Theo công thức Moa-vrơ ta có:
(cosα+i sinα )4=cos4α+i sin4 α
<=>(cos44α-6 sin2α cos2α+sin4α )+4(cos3α sinα-sin3α.cosα )i=cos4α+i sin4α
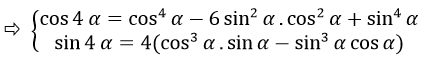
Bài 33 (trang 207 sgk Giải Tích 12 nâng cao):
Tính:
![]()
Lời giải:
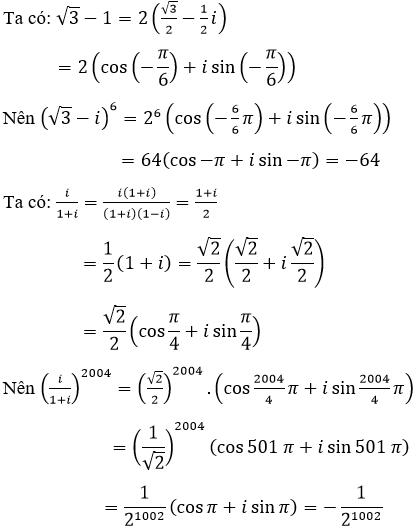
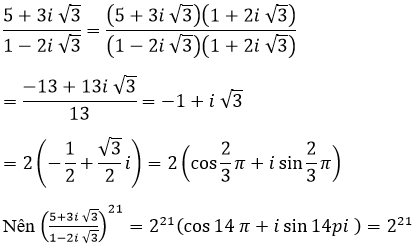
Bài 34 (trang 207 sgk Giải Tích 12 nâng cao):
Cho số phức
![]()
Tìm các số nguyên dương n để wn là số thực. hỏi có số nguyên dương m nào để wm là số ảo?
Lời giải:
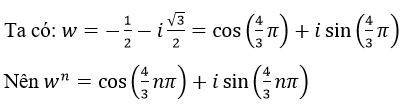
Để wn là số thực thì
![]()
Để n ∈N* thì k = 4 với t ∈N*. Khi đó n = 3t, với t ∈N*
Để wm là số ảo thì
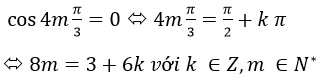
Vì Phương trình này vô nghiệm, nên không tồn tại m để wm là số ảo.
Bài 35 (trang 207 sgk Giải Tích 12 nâng cao):
Viết Phương trình lượng giác số phức z và của các căn bậc hai của z cho mỗi trường hợp sau:

Lời giải:
Giả sử z=r(cosα+i sinα)
a) Vì |z| = 3 => r = 3
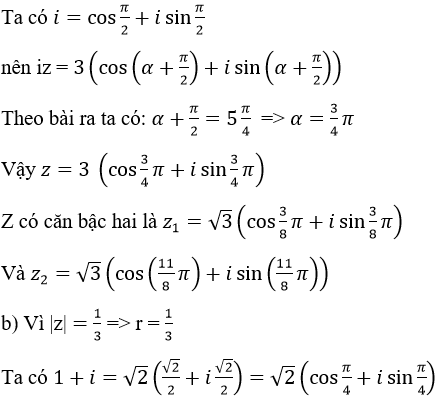
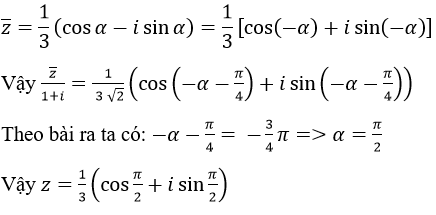
Z có hai căn bậc hai là:
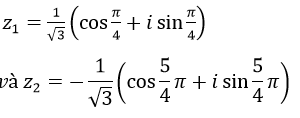
Bài 36 (trang 207 sgk Giải Tích 12 nâng cao):
Viết Phương trình dưới dạng lượng giác số phức:
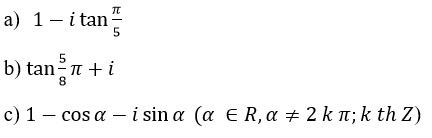
Lời giải: