Bài 1 (trang 189 sgk Giải Tích 12 nâng cao):
Cho số phức 2+3i;1+2i;2-i
a) Biểu diễn các số trong mặt phẳng số phức.
b) Viết số phức liên hợp của mỗi số đó và biểu diễn chúng trong mặt phẳng phức.
c) Viết đối số của mỗi số phức và biểu diến chúng trong mặt phẳng phức.
Lời giải:
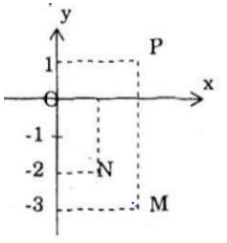
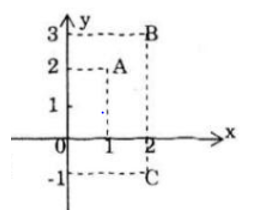
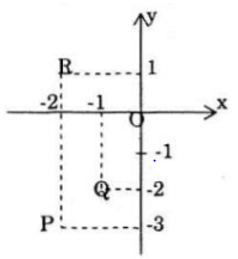
a) Các điểm A, B, C trong mặt phẳng tọa độ (hình vẽ) là biểu diến các số phức: 1 + 2i; 2 + 3i; 2 – i.

b) Số phức liên hợp của số z=2+3i là z− =2-3i
z’=1+2i là z’−=1-2i
z”=2-i là z−”=2+i
Các điểm M, N P biểu diễn cho các số z−, z−‘,z−” như sau: (hình vẽ)
c) Số đối của số phức: z=2+3i là-z=-2-3i
z’=1+2i là-z=-1-2i
z”=2-i là-z=-2+i
Các điểm P, Q, R lần lượt biển diễn cho các số -z, -z’, -z’’.
Bài 2 (trang 189 sgk Giải Tích 12 nâng cao)
Xác định phần thực và phần ảo các số sau:
a) i+(2-4i)-(3-2i) b) (√2+3i)2
c) (2+3i)(2-3i) d) i(2-i)(3+i)
Lời giải:
a) Ta có i+(2-4i)-(3-2i)=-i-1 có phần thức là -1 và phần ảo là -1
b) Ta có (√2+3i)2=2+6 √2 i+(3i)2=2+6 √2 i-9=-7+6 √2 i có phần thức là -7 và phần ảo là 6 √2
c) Ta có (2+3i)(2-3i)=4-6i+6i-9i2=4+9=13 có phần thức là 13 và phẩn ảo là 0.
d) i(2-i)(3+i)=i(6-i+1)=1+7i có phần thức là 1 và phần ảo là 7.
Bài 3 (trang 189 sgk Giải Tích 12 nâng cao):
Xác định các số phức biểu diễn bởi các đỉnh của một lục giác đều có tâm là gốc O trong mặt phẳng phức biết rằng một đỉnh biểu diễn số i.
Lời giải:
Gọi lục giác đều là ABCDEF, trong đó A là biểu diễn cho số i.
Suy ra A(0; 1) và góc AOB=60o (hình vẽ)
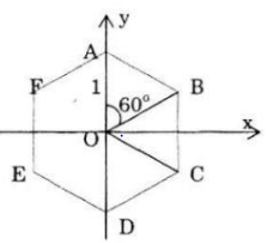
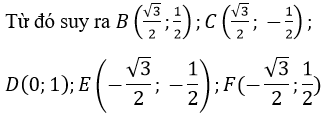
Vậy sáu số phức cần tìm là:
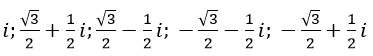
Bài 4 (trang 189 sgk Giải Tích 12 nâng cao):
Thực hiện phép tính:
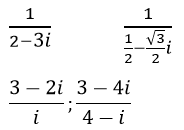
Lời giải:
Nhân cả tử và mẫu của số đã cho với lượng liên hợp ở mẫu ta được.
Bài 5 (trang 190 sgk Giải Tích 12 nâng cao):
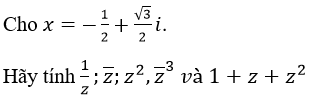
Lời giải:
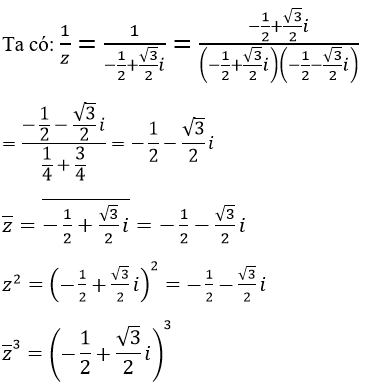
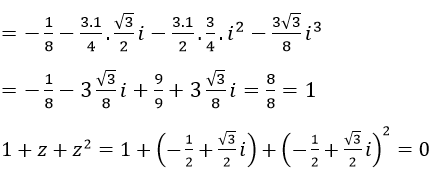
Bài 6 (trang 190 sgk Giải Tích 12 nâng cao):
Chứng minh
a) Phần thực của số phức z bằng 1/2(z+z− ), phần ảo của số phức z bằng 1/2i(z-z−)
b) Số phức z là phần ảo khi và chỉ khi z=-z−
c) Với mọi số phức z, z’ ta có
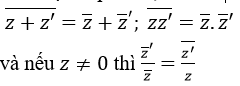
Lời giải:
a) Giả sử z=a+bi ta có z−=a-bi, nên
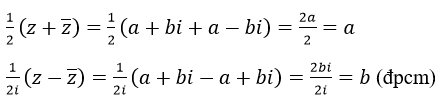
b) Giả sử z=a+bi
Theo bài ra z=-z− <=> a+bi=-(a-bi) <=> a=-a <=> a = 0
Vậy z = bi là một số ảo.
c) Giả sử z=a+bi,z’=a’+b’i. Ta có:
z+z’=(a+a’ )+(b+b’ )i => (z + z’)−=(a+a’ )-(b-b’ )i=(a-bi)+(a’-b’ i)=z−+z−‘ (đpcm)
z.z’=(a+bi)(a’+b’ i)=(aa’-bb’ )+(ab’+a’ b)i
=> zz’−=(aa’-bb’ )+(ab’+a’ b)i (1)
Và z−.z−‘=(a-bi)(a’-b’ i)=(aa’-bb’ )-(ab’+a’ b)i (2)
Từ (1) và (2) suy ra: zz’−=z−.z−‘ (đpcm)
Bài 7 (trang 190 sgk Giải Tích 12 nâng cao):
Chứng minh rằng với mọi số nguyên m > 0, ta có:
i4m=1;i4m+1;i4m+2=-1;i4m+3=-i
Lời giải:
Ta có: i4m=1=(i2 )2m=(-1)2m=1,với ∀m ∈N*
i4m+1=i4m.i=1.i=i
i4m+2=i4m.i2=1.(-1)=-1
i4m+3=i4m.i3=1.i3=i3=i2.i=-1.i=-i (đpcm)
Bài 8 (trang 190 sgk Giải Tích 12 nâng cao):
Chứng minh rằng:
a) Nếu vectơ u→ của một mặt phẳng phức biểu diễn số phức z thì độ dài của vectơ u→ là |u→ |=|z|, từ đó nếu các điểm A1;A2 theo thức tự biểu diễn các số phức z1;z2 thì |A1A2→ |=|z2-z1 |
b) Với mọi số phức z, z’ ta có |zz’ |=|z||z’ | và khi z ≠ 0 thì
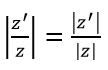
c) Với mọi số phức z, z’ ta có |z+z’ |≤|z|+|z’ |
Lời giải:
a) Nếu u→ là vectơ biểu diễn số phức z = a + bi thì u→=(a;b)
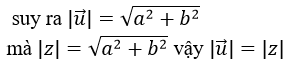
Gọi A1 là điểm biểu diễn số phức Z1=a1+b1 i=>A1 (a1;b1)
A2 là điểm biểu diễn số phức Z2=a2+b2 i=>A2 (a2;b2)
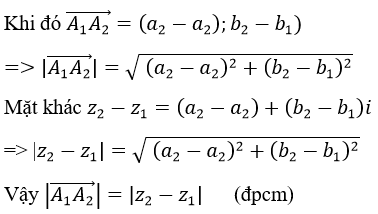
b) Ta có: z.z’=(a+bi)(a’+b’ i)=(aa’-bb’ )+(ab’+a’ b)i
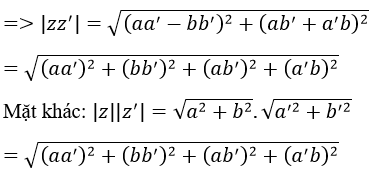
Vậy |zz’ |=|z||z’ |
Khi z ≠ 0 ta có:
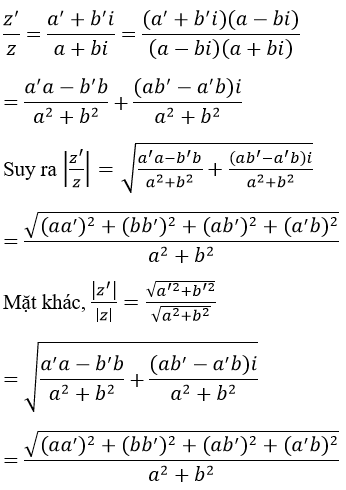
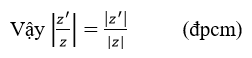
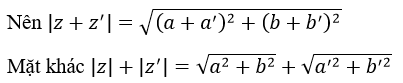
Theo yêu cầu bài toán ta cần chứng minh:
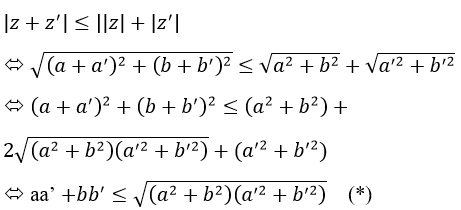
Theo Bu-nhi-cốp-xki ta có bất đẳng thức (*) đúng với ∀a,b,a’,b’∈R nên |z+z’ | ≤ ||z|+|z’ | (đpcm)
Bài 9 (trang 190 sgk Giải Tích 12 nâng cao):
Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn từng điều kiện sau:
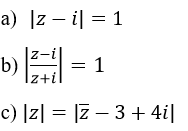
Lời giải:
a) Giả sử z=a+bi => z – I = a+(b-1)i
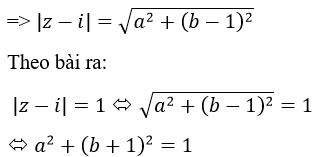
Vậy quỹ tích điểm M(a; b) biểu diễn số phức z=a+bi thõa mãn |z – i| =1 là đường tròn tâm I(0; 1), bán kính R = 1.
b) Giả sử z=a+bi
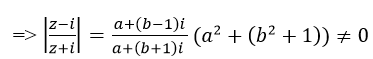
Theo bài 8b ta có:
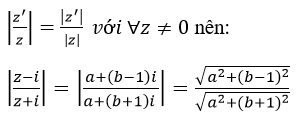
Theo bài ra ta có:
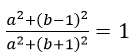
<=> a2+(b-1)2=a2+(b+1)2
<=> b = 0. Vậy z = a, hay tập hợp các điểm cần tìm là trục thực
Giả sử z=a+bi => z−=a-bi z−-3+4i=a-bi-3+4i=(a-3)+(4-b)i
Theo bài ra, ta có |z|=|z−-3+4i|<=> |z|=|(a-3)+(4-b)i|
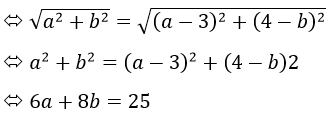
Vật quỹ tích điểm các điểm cần tìm trêm đường thẳng có phương trình 6a+8b=25 trong mặt phẳng phức (Oxy)