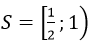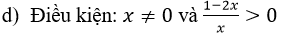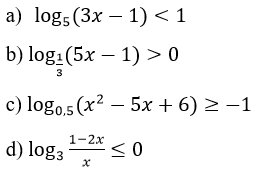
Bài 80 (trang 129 sgk Giải Tích 12 nâng cao): 

Giải các bất Phương trình

a) 2^3-6x > 1     b) 16^x > 0,125

Lời giải:

a) 2^3-6x > 1 <=> 2³ > 2^6x <=> 3 > 6x <=> x < 1/2

b) 16^x > 0,125 <=> 2^4x > 2^-3 <=> 4x > -3 <=> x > -3/4\

Bài 81 (trang 129 sgk Giải Tích 12 nâng cao): 

Giải các bất Phương trình sau

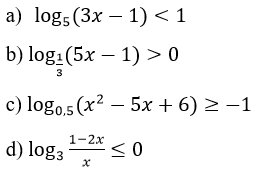
Lời giải:

a) log₅(3x-1) < 1.

Bất Phương trình <=> log₅(3x-1) < log₅⁡5 <=> 3x-1 < 5 <=> x < 2

Kết hợp với điều kiện ta được x < 2

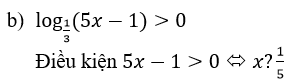
Bất Phương trình tương dương:

Kết hợp với điều kiện ta được:

c) log_0,5(x²-5x+6)≥ -1. Điều kiện: x²-5x+6)> 0

Bất phương trình tương dương với x²-5x+6 ≤ (0,5)^-1 <=> x²-5x+4 ≤ 0

<=> 1 ≤ x ≤ 4

Kết hợp với điều kiện ta được tập nghiệm S = [1; 2) ∪ (3; 4]

Cách khác: x²-5x+6 ≤ (0,5)^-1

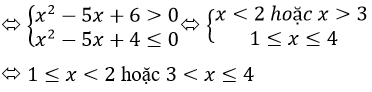
Tập nghiệm S = [1; 2) ∪ (3; 4]

Bất phương trình trên tương dương với

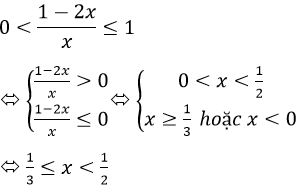
Tập nghiệm của bất phương trình là

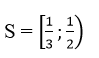
Bài 82 (trang 130 sgk Giải Tích 12 nâng cao): 

Giải các bất phương trình

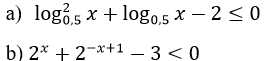
Lời giải:

a) Đặt t=log_0,5x-2

Ta được: t²+t-2 ≤ 0

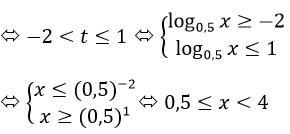
b) 2^x+2^-x+1-3 < 0 <=> 2^2x-3.2^x+2<0

Đặt t=2^x (t>0) ta được t²-3t+2<0 <=> 1<t<2

=> 1<2^x<2 <=> 0<x<1

Vậy tập nghiệm của Phương trình S = (0; 1)

Bài 83 (trang 130 sgk Giải Tích 12 nâng cao): 

Giải các bất phương trình:

a) log_0,1(x²+x-2)>log_0,1(x+3)    b) log_1/3(x²-6x+5)+2 log³(2-x) ≥ 0

Lời giải:

a) log_0,1(x²+x-2)>log_0,1(x+3)

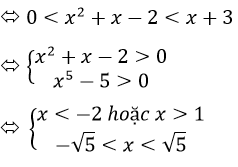
Vậy tập nghiệm của bất Phương trình là S=(-√5; -2)và (1;√5)

b) log_1/3(x²-6x+5)+2 log³(2-x) ≥ 0

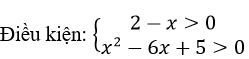
Ta có: log_1/3(x²-6x+5)+2 log³(2-x) ≥ 0

<=> log_1/3(x²-6x+5)≥log_1/3(2-x)²

<=> x²-6x+5≤(2-x)² <=> 2x-1≥0

Bất phương trình tương dương với:

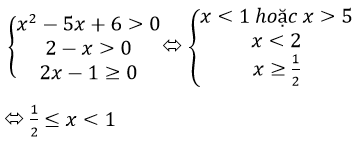
Vậy tập nghiệm của bất phương trình là:

Comments

comments