CÂU HỎI
Câu 1 (trang 34 sgk Vật Lí 12 nâng cao): Vẽ đồ thị li độ của dao động điều hòa sau đây (cùng dạng với đường liền nét (2) trong Hình 2.3): x = 2cos(πt – π/4) (cm)
Ghi rõ tọa độ giao điểm giao của đường biểu diễn với trục tung (x) và trục hoành (t).
Lời giải:
Học sinh tự vẽ theo dạng ở Hình 6.5 SGK
Câu 2 (trang 34 sgk Vật Lí 12 nâng cao): Xét ba đại lượng đặc trưng A, φ, ω cho dao động điều hòa của một con lắc lò xo đã cho. Những đại lượng nào có thể có những giá trị khác nhau, tùy thuộc cách kích thích dao động? Đại lượng nào chỉ có một giá trị xác định đối với con lắc lò xo đã cho?
Lời giải:
Trong ba đại lượng trên thì biên độ A, pha ban đầu φ là các đại lượng có thể có những giá trị khác nhau, tùy thuộc cách kích thích dao động. Còn tần số góc ω chỉ có một giá trị xác định đối với con lắc lò xo đã cho và luôn bằng ω = √(k/m).
Câu 3 (trang 34 sgk Vật Lí 12 nâng cao): Nói rõ về thứ nguyên của các lượng A, φ, ω.
Lời giải:
– Thứ nguyên của các đại lượng A là chiều dài (m, cm …)
– Đại lượng φ là góc nên không có thứ nguyên.
– Thứ nguyên của đại lượng [ω] = 1/T ⇒ thứ nguyên là nghịch đảo của thời gian (1/s hay s(-1))
BÀI TẬP
Bài 1 (trang 34 sgk Vật Lí 12 nâng cao): Tốc độ của chất điểm giao động điều hòa cực đại khi:
Li độ cực đại B. gia tốc cực đại
C. li độ bằng 0 D. pha bằng π/4
Lời giải:
Chọn C
Bài 2 (trang 35 sgk Vật Lí 12 nâng cao): Gia tốc của chất điểm dao động điều hòa bằng 0 khi:
A. Li độ cực đại B. li độ cực tiểu
C. Vận tốc cực đại hoặc cực tiểu D. vận tốc bằng 0.
Lời giải:
Chọn C
Bài 3 (trang 35 sgk Vật Lí 12 nâng cao): Dao động cơ điều hòa đổi chiều khi:
A. Lực tác dụng đổi chiều B. lục tác dụng bằng 0
C. lực tác dụng có độ lớn cực đại D. lực tác dụng có độ lớn cực tiểu.
Lời giải:
Chọn C
Bài 4 (trang 35 sgk Vật Lí 12 nâng cao): a) Thử lại rằng:
x = A1cosωt + A2sinωt (6.14)
trong đó A1 và A2 là hai hằng số bất kì cũng là nghiệm của phương trình (6.3).
b) Chứng tỏ rằng, nếu chọn A1 và A2 trong biểu thức ở vế phải của (6.14) như sau:
A1 = A.cosφ; A2 = -Asin φ
thì biếu thức ấy trùng với biểu thức ở vế phải của (6.4).
Lời giải:
a) Thử lại rằng: x = A1 cosωt + A2sinωt (6.14)
Trong đó A1; A2 là hai hằng số bất kì cũng là nghiệm của Phương trình (6.3)
Ta có : x’= -ωA1sinωt + ωA2cosωt
Suy ra : x”= -ω2A1cosωt – ω2A2sinωt (6.15)
thay (6.15) và (6.14) vào Phương trình (6.3) x”+ ω2x = 0 ta thấy nghiệm đúng.
b) Nếu chọn A1 và A2 trong biểu thức ở vế phải của (6.14) như sau.
A1 = Acosφ; A2 = -Asinφ.
Thay A2 và A1 bằng các giá trị đã chọn vào (6.14) ta được:
x = A1 cosωt + A2sinωt
= Acosφcos[ωt] – Asinφsinωt = Acos(ωt + φ)
Bài 5 (trang 35 sgk Vật Lí 12 nâng cao): Phương trình dao động của một vật là: x = 6 cos(4 πt + π/6) (cm)
Xác định biên độ, tần số góc, chu kì tần số của dao động.
Xác định pha dao động tại thời điểm t = 1/4 s, từ đó suy ra li độ tại thời điểm ấy.
Vẽ vectơ quay biểu diễn dao động vào thời điểm t = 0.
Lời giải:
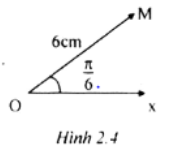
Biên độ 6 cm, tần số góc là 4 π, chu kì T=(2 π)/ω = 0,5s, tần số 2 Hz.
Pha 4 π.1/4 + π/6 = 7/2 π rad, li độ x = 6 cos[7/6 π] = -3√3 cm
Độ dài vectocm, góc hợp với Ox là π/6

Bài 6 (trang 35 sgk Vật Lí 12 nâng cao): Một vật dao động điều hòa với biên độ A = -4 cm và chu kì T = 2s.
a) Viết phương trình dao động của vật, chọn gốc thời gian là lúc nó đi qua vị trí cân bằng theo chiều dương.
b) Tính li độ của vật tại thười điểm t = 5,5s.
Lời giải:
a) Dạng tổng quát của Phương trình dao động là x = Acos (ωt + φ)
Biên độ A = -4cm.
Tần số góc ω = 2πf = π (rad/s)
Pha ban đầu φ xác định bởi điều kiện ban đầu (chọn gốc thời gian):
T = 0 thì x(0) = 0; v(0) = x’(0) > 0
Suy ra cosφ = 0; -sinφ > 0 tức là φ = -π/2.
Vậy ta được: x = 4 cos(πt-π/2) (cm )
b) t = 5,5s thì x = 4 cos 5π = -4cm
Bài 7 (trang 35 sgk Vật Lí 12 nâng cao): Một vật nặng treo vào lò xo làm cho lò xo dãn ra 0,8 cm. Cho vật dao động. Tìm chu kì dao động ấy. Lấy g = 10 m/s2.
Lời giải:
Chu kì dao động T = 2 π √(m/k), m là khối lượng của vật, k là độ cứng của lò xo.
Xét điều kiện cân bằng của vật ta có:
mg = k∆l
⇒m.10 = k.0,008
Vậy m/k = 0,008/100 = [8.10](-4)
T = 2 π √([8.10](-4) ) = 2π2 √2.[10](-2) ≈ 0,18s