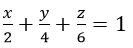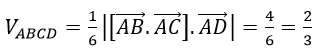
Bài 1 (trang 109 sgk Hình Học 12 nâng cao):
Cho bốn điểm A(1, 6, 2), B(4, 0, 6); C(5, 0, 4), D(5, 1, 3).
a) Chứng minh rằng bốn điểm đó không đồng phẳng.
b) Tính thể tích tứ diện ABCD.
c) Viết Phương trình mp(BCD)
d) Viết Phương trình mặt cầu tâm A tiếp xúc với mp(BCD). Tìm tọa độ tiếp điểm.
Lời giải:
a) Ta có: AB→=(3,-6,4);AC→=(4,-6,2),AD→=(4,-5,1)nên [AB→.AC→ ].AD→=4 ≠ 0. Suy ra A, B, C, D không đồng phẳng.
b) Thể tích tứ diện ABCD là:
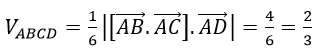
c) Mặt phẳng (BCD) là mặt đi qua B(4, 0, 6) và nhận vectơ [BC→BD→] là vectơ pháp tuyến.
Ta có BC→=(1,0,-2);BD→=(1,1,-3), suy ra [BC→BD→ ]=(2,1,1) nên mp(BCD) có phương trình là:
2(x-4)+y+(z-6)=0 <=> 2x+y+x-14=0
d) Mặt cầu tâm A(1, 6, 2) tiếp xúc với mp(BCD) có bán kính là
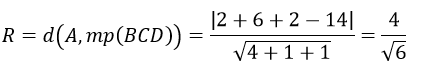
Nên mặt cầu có phương trình là: (x-1)2+(y-6)2+(z-2)2=8/3
Tiếp điểm H của mặt cầu với mp(BCD) chính là hình chiếu vuông góc của tâm A(1, 6, 2) lên mp(BCD)
Để tìm tọa độ điểm H trước hết ta viết phương trình đường thẳng Δ đi qua A và Δ ⊥ (BCD))
Δ đi qua A(1, 6, 2) và nhận vectơ pháp tuyến của mp(BCD) là n→=(2,1,1)là vectơ chỉ phương, nên Δ có phương trình
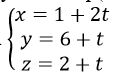
Khi đó H là giao điểm của Δ và mp(BCD), nên tọa độ của H là nghiệm của hệ
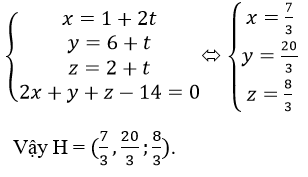
Bài 2 (trang 109 sgk Hình Học 12 nâng cao):
Cho hai điểm A(1, -1, -2); B(3,1, 1) và mp(P): x-2y+3z-5=0
a) Tìm tọa độ điểm A’ đối xứng với A qua mp(P).
b) Tìm góc giữa đường thẳng AB và mp(P).
c) Viết phương trình mp(Q) đi qua A, B và vuông góc với mp(P).
d) Tìm tọa độ giao điêm I của đường thẳng AB và mp(P). viết phương trình đường thẳng Δ nằm trong (P), đi qua I và vuông góc với AB.
Lời giải:
a) + Viết Phương trình đường thẳng d đi qua A và (d) ⊥ mp(P).
Đường thẳng (d) đi qua A(1, -1, -2) và nhận vectơ pháp tuyến của mp(P) là n→=(1,-2,3) là vectơ chỉ phương, nên đường thẳng (d) có phương trình

+ Tìm tọa độ giao điểm H của d và mp(P)
Tọa độ của H là nghiệm của hệ:
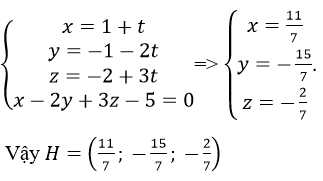
+ Vì A và A’ đối xứng với nhau qua mp(P) nên H chính là trung điểm của AA’, ta có:
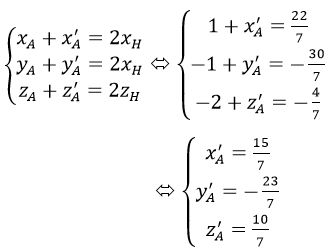
b) Ta có (AB) ⃗=(2,2,3), vectơ pháp tuyến của mp(P) là n→=(1,-2,3) nên góc giữa AB và mp(P) xác định như sau:
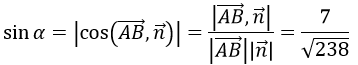
c) Mặt phẳng (Q) đi qua AB vuông góc với mp(P) là mặt phẳng đi qua A(1, -1, -2) và nhận vectơ [AB→,n→ ]=(12,-3,6) làm vectơ pháp tuyến, nên mp(Q) có phương trình là:
12(x-1)-3(y+1)-6(z+2)=0 <=> 4x-y-2z-9=0
d) Đường thẳng AB có phương trình:

nên tọa độ giao điểm I của đường thẳng AB và mp(P) là nghiệm của hệ
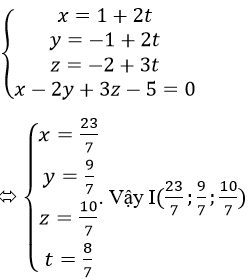
Vì đường thẳng Δ nằm trogn mp(P) và Δ ⊥ AB nên Δ nhận vectơ u→=[n→,AB→] làm vectơ chỉ Phương, với AB→=(2,2,3), n→=(1,-2,3) là vectơ pháp tuyến của mp(P).
Ta tính được u→=[n→,AB→ ]=(-12,3,6)
Nên phương trình của đường thẳng Δ là
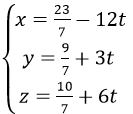
Bài 3 (trang 109 sgk Hình Học 12 nâng cao):
Cho đường thẳng d và mp(P) có phương trình:
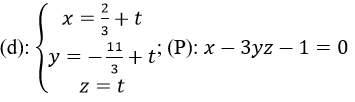
a) Viết Phương trình đường thẳng d’ là hình chiếu vuông góc của d trên mp(P).
b) Viết phương trình đường thẳng d1 là hình chiếu của d trên mp(P) theo phương Oz.
c) Viết Phương trình đường thẳng đi qua gốc tọa độ O, cắt d và song song với mp(P).
Lời giải:
a) Hình chiếu d’ của d lên mp(P) là giao tuyến của (P) và (Q), trong đó (Q) là mặt phẳng chứa d và (q) vuông góc với (P). mặt phẳng (Q) đi qua
![]()
Δd nhận vectơ [u→,n→]=(4,0,-4), nên mp(Q) có phương trình là:
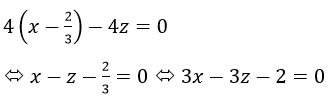
Vậy Phương trình tổng quát của đường thẳng (d’) là:
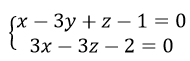
b) Hình chiếu d1 của d trên mp(P) theo Phương Oz là giao tuyến của mp(P) và mp(R), trong đó mp(R) là mặt phẳng chứa d và song song với Oz.
Mặt phẳng (R) đi qua M0 (2/3;-11/3;0)∈d và nhận vectơ [u1→,k→ ] làm vectơ pháp tuyến, trong đó u1→=1,1,1) là vectơ chỉ Phương của d và k→=(0,0,1) là vectơ chỉ Phương của Oz, ta tính được [u1→,k→ ]=(1; -1;0). Vậy mp(R ) có Phương trình là:
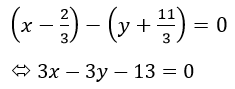
Suy ra Phương trình tổng quát của đường thẳng (d1) là:
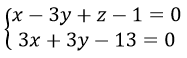
c) Gọi Δ là đường thẳng đi qua gốc tọa đọ O, cắt d và song song với mp(P). khi đó Δ là giao tuyến của hai mặt (α)và (β) là mặt phẳng đi qua O và song song với mp(P).
Mặt phẳng (α) có Phương trinh: -11x-2y+13z=0
Mặt phẳng (β) có phương trình: x-3y+z=0
Vậy đường thẳng Δ có Phương trình tổng quát là:
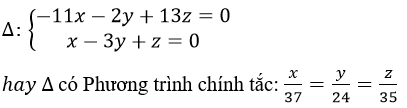
Bài 4 (trang 110 sgk Hình Học 12 nâng cao):
Cho điểm A(2, 3, 1) và hai đường thẳng:
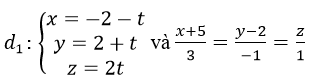
a) Viết Phương trình mp(P) đi qua A và d1
b) Viết Phương trình mp(Q) đi qua A và d2.
c) Viết Phương trình đường thẳng d đi qua A cắt 1 và d2.
d) Tính khoảng cách từ A đến d2.
Lời giải:
a) Đường thẳng d1d đi qua M1 (-2;2;0) và có vectơ chỉ phương n1→=(-1;1;2)
Mặt phẳng (P) đi qua A và cắt d1 là mặt phẳng đi qua A(2; 3; 1) và nhận [AM1→,n1→ ]=(-1;9; -5) làm vectơ pháp tuyến, nên mp(P) có phương trình:
-(x-2)+99y-3)-5(z-1)=0 <=> -x+9y-5z-20=0
b) Đường thẳng d2 đi qua M2 (-5;2;0) và có vectơ chỉ phương n2→=(3; -1;1)
Mặt phẳng (Q) đi qua A và d2 sẽ nhận vectơ [AM2→,n2→]=(-2;4;10) làm vectơ pháp tuyến, nên mp(Q) có Phương trình:
-2(x-2)+4(y-3)+10(z-1)=0 <=> -2x+4y+10z-18=0 <=> x-2y-5z+9=0
c) Đường thẳng d đi qua A cắt d1 và d2 là giao tuyến của mp(P) và mp(Q) nên d có Phương trình tổng quát:
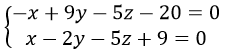
d) Khoảng cách từ A đến d2, được xác định như sau:
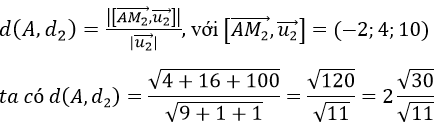
Bài 5 (trang 110 sgk Hình Học 12 nâng cao):
Cho hai đương thẳng:
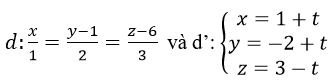
a) Chứng minh hai đường thẳng chéo nhau. Tìm góc giữa chúng.
b) Tìm khoảng cách giữa d và d’.
c) Viết Phương trình vuông góc chung của d và d’.
d) Viết phương trình đường thẳng song song với Oz, cắt cả d và d’.
Lời giải:
Giải
Đường thẳng d đi qua M(0; 1; 6) và có vectơ chỉ phương u→=(1,2,3)
d’ đi qua M’(1; -2; 3) và có vectơ chỉ Phương u’→=(1;1; -1)
a) Ta có MM’→=(1; -3; -3),[u→,u’→ ]=(-5;4; -1)
Suy ra [u→,u’→ ].MM’→=-14 ≠ 0 nên d và d’ chéo nhau.
Ta có
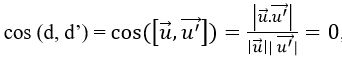
Vậy d ⊥ d’.
b) Ta có [u→,u’→ ]=(-5;4; -1),[u→,u’→ ].MM’→=-14 (theo câu a)
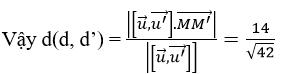
c) Theo câu a, ta có d⊥d’, vậy đường vuông góc của d và d’chính là giao tuyến của mp(P) và mp(Q). Trong đó mp(P) chứa d và vuông góc với d’, mp(Q) chứa d’ và vuông góc với d.
Phương trình mp(P) là: 1(x-0)+1(y-1)-1(z-6)=0
<=> x+y-z+5=0
Phương trình mp(Q) là: 1(x-1)+2(y-2)+3(z-3)=0
<=> x+2y+3z-6=0
Vậy Phương trình đường vuông góc chung của d và d’ là:
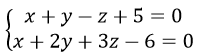
hoặc có phương trình tham số là:
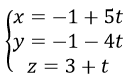
d) Đường thẳng song song với OZ và cắt cả d và d’ là giao tuyến của mp(α) và mp(β);
Trong đó (α) là mặt phẳng chứa d và song song với Oz.
(β) là mặt phẳng chứa d’ và song song với Oz.
Đường thẳng Oz có vectơ chỉ Phương là k→=(0;0;1)
Mặt phẳng (α) đi qua M(0; 1; 6) và nhận [u→,k→]=(2; -1;0) làm vectơ pháp tuyến nên α có Phương trình là: 2x-y+1=0
Tương tự mp(β) có Phương trình: x – y- 3 =0
Vậy Phương trình đường thẳng cần tìm là:
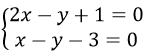
Hay có Phương trình tham số là:
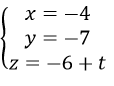
Bài 6 (trang 110 sgk Hình Học 12 nâng cao):
Cho hai đường thẳng:
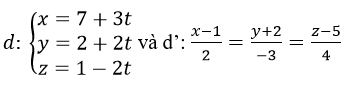
a) Chứng minh rằn d và d’ đồng phẳng. viết phương trình mặt phẳng (P) chứa chúng.
b) Tính thể tính hình tứ diện giới hạn bởi mp(P) và ba mặt phẳng tọa độ.
c) Viết phương trình mặt cầu ngoại tiếp tứ diện nói trên.
Lời giải:
a) Đường thẳng d đi qua M(7; 2; 1) và có vectơ chỉ phương u→=(3;2; -2) d’ đi qua M’(1; -2; 5) và có vectơ chỉ phương u’→=(2; -3;4)
Ta có [u→,u’→ ]=(2; -16; -13), MM’→=(-6; -4;4)
Mặt phẳng (P) chứa d và d’ có vectơ pháp tuyến là [u→,u’→ ]=(2; -16; -13) đi qua (P) đi qua M(7; 2; 1) ∈d nên (P) có phương trình là:
2(x-7)-16(y-2)-13(z-1)=0 <=> 2x-16y-13z+31=0
b) Mặt phẳng (P) cắt Ox tại A(-31/2;0;0); cắt Oy tại B(0;31/16;0); cắt Oz tại C(0;0;31/13). Suy ra thể tích tứ diện cần tìm là:

c) Viết Phương trình mặt cầu đi qua 4 điểm O, A, B, C.
Gọi Phương trình mặt cầu là: x2+y2+z2+ax+ay+cz+d=0
Vì mặt cầu đi qua O(0; 0; 0) nên d = 0’
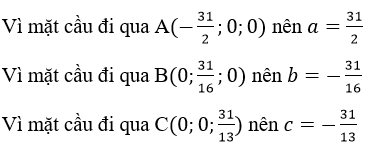
Vậy Phương trình mặt cầu là:
![]()
Bài 7 (trang 111 sgk Hình Học 12 nâng cao):
Cho hai đường thẳng:
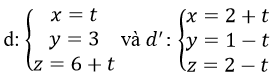
a) Chứng minh rằng d và d’ chéo nhau và vuông góc với nhau.
b) Viết Phương trình mp(P) đi qua d và vuông góc với d’, phương trình của mp(Q) đi qua d’ và vuông góc với d.
c) Viết Phương trình chính tắc của đường vuông góc chung của d và d’
Lời giải:
Đường thẳng d đi qua M(0; 3; 6) và có vectơ chỉ phương u→=(1;0;1)
d’ đi qua M'(2;1;2) và có vectơ chỉ Phương (u’→=(1; -1; -1)
a) Ta có [u→,u’→ ]=(1;2; -1);MM’→=(2; -2; -4) nên [u→,u’→ ].MM’→=2 ≠ 0 nên d và d’ chéo nhau.
Mặt khác [u→,u’→ ]=0 nên d và d’ vuông góc với nhau.
b) Mặt phẳng (P) đi qua d và vuông góc với d’ nên (P) đi qua điểm M(0; 3; 6) ∈dvà nhận vectơ chỉ Phương của d’ là (u’) ⃗=(1; -1; -1) làm vectơ pháp tuyến. vậy mp(P) có phương trình là:
(x-0)-(y-3)-(z-6)=0 <=> x-y-z+9=0
Tương tự, ta viết được phương trình mặt phẳng (Q) là: x + z – 4 = 0
c) Vì d và d’ vuông góc với nhau nên đường thẳng vuông góc chung Δ) của d và d’ chính là giao tuyến của (P) và (Q). theo cầu b, ta có Phương trình tổng quát của (Δ) là:
![]()
Chuyển về Phương trình chính tắc ta được.
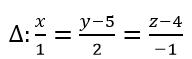
Bài 8 (trang 111 sgk Hình Học 12 nâng cao):
Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình:
(P): 2x-y+z+2=0 và (Q): x-y+2z-1=0
a) chứng minh rằng (P) và (Q) cắt nhau. Tìm góc giữa hia mặt phẳng đó.
b) viết phương trình đường thẳng d đi qua A(1; 2; -3), song song với cả (P) và (Q).
c) viết phương trình mp(R) đi qua B(-1; 3; 4), vuông góc với cả (P) và (Q).
Lời giải:
a) Mp(P) có vectơ pháp tuyến n1→=(2; -1;1)
Mp(Q) có vectơ pháp tuyến n2→=(1;1;2)
Ta có: [n1→,n2→]=)-3; -3;3) ≠ 0→ , vậy (P) và (Q) cắt nhau.
Ta có
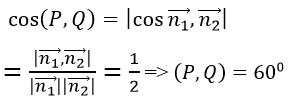
b) Đường thẳng d đi qua A(1; 2; -3) và song song với cả (P) và (Q) là đường thẳng đi qua A(1; 2; -3) và nhận[n1→,n2→]=(-3; -3;3) là, vectơ chỉ phương, vậy Phương trình của d là:
c) Mặt phẳng (R ) đi qua B(-1, 3, 4) và vuông góc với cả (P) và (Q) là mặt phẳng đi qua B(-1; 3; 4) và nhận[n1→,n2→ ]=(-3; -3;3) làm vectơ pháp tuyến.
Vậy (R ) có phương trình là: -3(x+1)-3(y-3)+3(z-4)=0
<=> x+y-z+2=0
Bài 9 (trang 111 sgk Hình Học 12 nâng cao):
Cho mặt cầu (S) có phương trình: x2+y2+z2-2x-4y-6z=0
a) Tìm tọa độ tâm mặt cầu và tính bán kính mặt cầu.
b) Tùy theo giá trị của k, xét vị trị tương đối của mặt cầu (S) và mp(P) với (P): x+y-z+k=0
c) Mặt cầu cắt ba trục Ox, Oy, Oz lần lượt tại ba diểm A, B, C khác với góc tọa độ O. Viết Phương trình mp(ABC).
d) Viết phương trình mặt phẳng tiếp xúc với mặt cầu (S) tại điểm B.
e) Viết Phương trình mặt phẳng tiếp xúc với mặt cầu (S) và song song với mặt phẳng (Q): 4x+3y-12z-1=0
Lời giải:
a) Phương trình: x2+y2+z2-2x-4y-6z=0
(x-1)2+(y-2)2+(z-3)2=14
Vậy mặt cầu (S) có tâm là I = (1; 2; 3), bán kính R = √14
b) Tính khoảng cách từ tâm I(1; 2; 3) của mặt cầu (S) đến mặt phẳng (P) là:
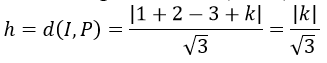
thì (P) là mặt phẳng tiếp xúc với mặt cầu.
![]()
thì mp(P) và mặt cầu (S) không có điểm chung.
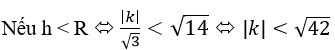
thì mp(P) cắt mặt cầu (S)
c) Mặt cầu (S) cắt trục Ox tại A(2; 0; 0) và O(0; 0; 0)
(S) cắt trục Oy tại B(0; 4; 0) và O(0; 0; 0)
(S) cắt trục Oz tại C(0; 0; 6) và O(0; 0; 0)
Vậy mặt phẳng (ABC) có phương trình:
d) Mặt phẳng tiếp xúc với mặt cầu (S) tại điểm B(0; 4; 0) là mặt phẳng đi qua B(0; 4; 0) và có vectơ pháp tuyến là BI→=(1; -2;3), vậy Phương trình của mặt phẳng đó là: (x-0)-2(y-4)+3(z-0)=0 <=> x-2y+3z+8=0
e) Vì mặt phẳng cần tìm song song với mp(Q): 4x+3y-12z-1=0 nên có dạng: 4x+3y-12z+D=0 (α)
Vì mặt tiếp xúc với mặt cầu (S) nên ta có:
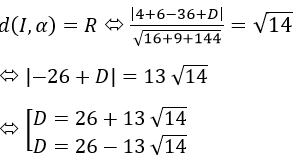
Vậy mặt phẳng cần tìm có Phương trình là: 4x+3y-12z+26+13√14=0 hoặc 4x+3y-12z+26-13√14=0
Bài 10 (trang 111 sgk Hình Học 12 nâng cao):
Cho hình lập Phương ABC.A’B’C’D’ có cạnh bằng 1. Trên các tỉa AA’, AB, AD (có chung gốc A) lần lượt lấy các điểm M, N, P khác A sao cho AM = m, AN = n và AP = p.
a) Tìm sự liện hẹ giữa m, n, p sao cho mp(MNP) đi qua đỉnh C’ của hình lập Phương.
b) Trong trường hợp mp(MNP) luôn đi qua C’, hãy tìm thể tích bé nhật của tứ diện AMNP. Khi đó tứ diện AMNP có tính chất gì?
Lời giải:
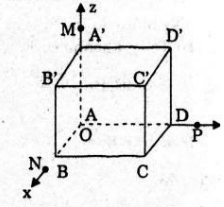
Chọn hệ trục tọa độ Oxyz sao cho A = O; Ox, Oy, Oz lần lượt chứa các tia AB, AD, AA’. Khi đó C’ ≡(1,1,1),M(0;0;m);N(n,0,0);P(0;p;0) với m, n, p dương.
a) Mặt phẳng (MNP) có phương trình viết theo đoạn chắn.
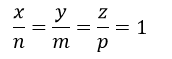
Để mp(MNP) đi qua điểm C’(1; 1; 1) thì:
![]()
b) Thể tích tứ diện AMNP là

Theo bất đẳng thức cô – si, ta có:
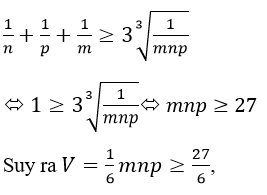
dấu “=” xảy ra khi m = n = p = 3.
Vậy thể tích bé nhất của tứ diện AMNP khi mp(MNP) đi qua C’ là 27/6 tương ứng với m = n = p = 3.