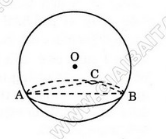
Bài 1 (trang 50 SGK Hình học 12): Cho ba điểm A, B, C cùng thuộc một mặt cầu sao cho (ACB)=90o.Trong các khẳng định sau, khẳng định nào đúng?
a) Đường tròn qua ba điểm A, B, C nằm trên mặt cầu.
b) AB là một đường kính của mặt cầu đã cho.
c) AB không phải là đường kính của mặt cầu.
d) AB là đường kính của đường tròn giao tuyến tạo bởi mặt cầu và mặt phẳng (ABC).
Lời giải:
a) Đúng
b) Sai
c) Sai
d) Đúng.


Bài 2 (trang 50 SGK Hình học 12): Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC. Biết AB = AD = a. Tính diện tích xung quanh của hình nón và thể tích của khối nón được tạo thành khi quay đường gấp khúc BDA quanh cạnh AB.
Lời giải:
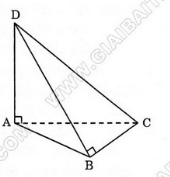

Bài 3 (trang 50 SGK Hình học 12): Một hình chóp có tất cả các cạnh bên bằng nhau. Chứng minh rằng hình chóp đó nội tiếp được trong một mặt cầu (các đỉnh của hình chóp nằm trên mặt cầu).
Lời giải:
Cho hình chóp S.A1A2A3…An có các cạnh bên bằng nhau.
Giả sử I là hình chiếu vuông góc của S trên mặt đáy.
Ta có: SA1 = SA2 = SA3 = … = SAn
Suy ra ΔSIA1= ΔSIA2 = ΔSIA3 = … = ΔSIAn
Suy ra IA1 = IA2 = IA3 = … = IAn
Đa giác A1A2A3…An là một đa giác nội tiếp được trong một đường tròn tâm I bán kính IA, trục SI.
Trong mp(SAI), đường trung trực của SA1 cắt SI tại O, ta có:
OS = OA1 (1)
OA1 = OA2 = OA3 = … = OAn (2)
Từ (1) và (2) suy ra OS = OA1 = OA2 = OA3 = … = OAn
Vậy hình chóp S.A1A2A3…An nội tiếp được trong một mặt cầu.
Bài 4 (trang 50 SGK Hình học 12): Hình chóp S.ABC có một mặt cầu tiếp xúc với các cạnh bên SA, SB, SC. Mặt cầu này còn tiếp xúc với ba cạnh AB, BC, CA tại trung điểm của mỗi cạnh. Chứng minh rằng hình chóp đó là hình chóp tam giác đều.
Lời giải:
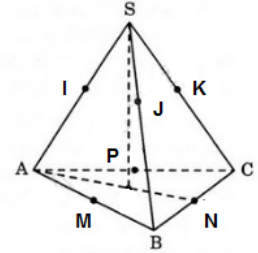
Gọi M, N, P lần lượt là trung điểm của AB, BC, CA; I, J, K là tiếp điểm của các cạnh bên SA, SB, SC với mặt cầu.
Ta có: AM = AI và BM = BJ
Mà AM = BM nên AI = BJ
Mặt khác SI = SJ
Nên SI + AI = SJ + BJ
Vậy SA = SB (1)
Tương tự, ta có: SB = SC (2)
Từ (1) và (2) => SA = SB = SC (3)
Mặt khác BM = BN và CN = CP
Suy ra AB = 2BM = BC = 2CN = 2CP = CA
Khi đó ABC là tam giác đều (4)
Từ (3) và (4) suy ra S.ABC là hình chóp tam giác đều.
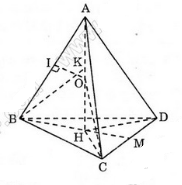
Bài 5 (trang 50 SGK Hình học 12): Cho tứ diện đều ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD).
a) Chứng minh H là tâm đường tròn ngoại tiếp tam giác BCD. Tính độ dài đoạn AH.
b) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ có đường tròn đáy ngoại tiếp tam giác BCD và chiều cao AH.
Lời giải:

Bài 6 (trang 50 SGK Hình học 12): Cho hình vuông ABCD cạnh a. Từ tâm O của hình vuông dựng đường thẳng Δ vuông góc với mặt phẳng (ABCD). Trên Δ lấy điểm S sao cho OS = a/2 . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.
Lời giải:


Bài 7 (trang 50 SGK Hình học 12): Cho hình trụ có bán kính r, trục OO’ = 2r và mặt cầu đường kính OO’.
a) Hãy so sánh diện tích mặt cầu và diện tích xung quanh của hình trụ.
b) Hãy so sánh thể tích khối trụ và thể tích khối cầu được tạo nên bởi hình trụ và mặt cầu đã cho.
Lời giải:
