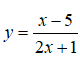
Câu 15: Cho hàm số

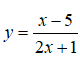
Đồ thị hàm số có tiệm cận ngang là

A. y = 1   B. y = 0   C. y = 1/2   D. y = -5

Câu 16: Số nghiệm của phương trình |x³| – 12|x| = m (với -1 < m < 0 ) là

A. 1    B. 2   C. 3    D. 4.

Câu 17: Cho hai số dương a, b thỏa mãn a² + b² = 7ab. Đẳng thức nào sau đây đúng?

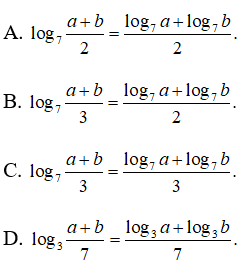
A. 1    B. 2    C. 3    D. 4.

Câu 18: Số nghiệm của phương trình log_1/4(x² – x⁴) = 1 là

A. 1    B. 2   C. 3    D. 4.

Câu 19: Giả sử x là nghiệm của phương trình:

Khi đó ta có:

A. lg(1 – x) = 1   B. lg(1 – x) = √3

C. lg(1 – x) < 1    D. lg(1 – x) > √3

Câu 20: Tập nghiệm của phương trình 3^{2x + 1} – 4.3^{x + 1} + 9 ≤ 0 là

A. x ≥ 0   B. x ≤ 1     C. 0 ≤ x ≤ 1    D. 0 ≤ x ≤ 2

Hướng dẫn giải và Đáp án

15-C

16-D

17-B

18-B

19-D

20-C

Câu 15:

Ta có

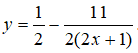
Suy ra:

Vậy đồ thị hàm số có tiệm cận ngang là y = 1/2

Câu 16:

Số nghiệm của phương trình |x³| – 12|x| = m là số giao điểm của đường thẳng d: y = m với đồ thị hàm số y = |x³| – 12|x|. Dựa vào đồ thị suy ra với -1 < m < 0 thì phương trình có 4 nghiệm.

Câu 17:

Ta có: a² + b² = 7ab

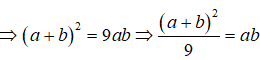
Lấy logarit cơ số 7 hai vế ta có

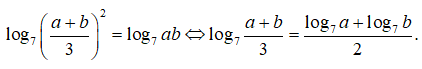
Câu 18:

Ta có: log_1/4(x² – x⁴) = 1

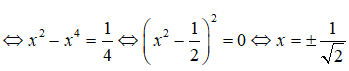
Vậy phương trình có hai nghiệm.

Câu 19:

Điều kiện: -1 < x < 1. Ta có:

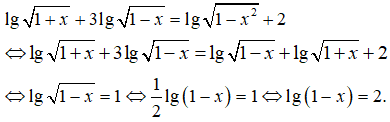
Do đó lg(1 – x) > √3

Câu 20:

Đặt t = 3^x (t > 0). Bất phương trình đã cho trở thành

3t² – 12t + 9 ≤ 0 <=> 1 ≤ t ≤ 3

Suy ra 1 ≤ 3^x ≤ 3

Vậy tập nghiệm của bất phương trình là 0 ≤ x ≤ 1

Comments

comments