Câu 8: Số điểm cực tiểu của hàm số y = x4 + x2 + 1 là
A. 0 B. 1 C. 2 D. 3.
Câu 9: Cho hàm số y = x3 – 3x2 + 1. Tích các giá trị cực đại của hàm số là
A. 0 B. –3 C. 3 D. –6
Câu 10: Đường thẳng đi qua hai điểm cực trị của hàm số y = x3 – 3x2 + 2 có phương trình là
A. y = -x + 2 B. y = x + 2 C. y = 2x + 2 D. y = -2x + 2
Câu 11: Hàm số y = x3 – 6x2 có giá trị nhỏ nhất và giá trị lớn nhất trên đoạn [-1; 5] tương ứng là
A. –25 và –7 B. –7 và 0 C. –32 và 0 D. –32 và –7.
Câu 12: Tiếp tuyến tại điểm A(0; 2) của đồ thị hàm số y = x3 – 3x + 2 có phương trình là
A. y = -3x + 2 B. y = 3x + 2 C. y = 2x + 2 D. y = x + 2
Câu 13: Cho hàm số y = 2x4 – 5x2 – 7. Số tiếp tuyến đi qua điểm M(0; -7) của đồ thị hàm số là
A. 1 B. 2 C. 3 D. 4
Câu 14: Số giao điểm của đồ thị hàm số y = x3 – 3x2 + 2x + 1 với trục hoành là
A. 0 B. 1 C. 2 D. 4
Hướng dẫn giải và Đáp án
| 8-B | 9-B | 10-D | 11-C | 12-A | 13-C | 14-B |
Câu 8:
Ta có: y’ = 4x3 + 2x = 2x(2x2 + 1) . Do đó: y’ = 0 <=> x = 0 Lập bảng biến thiên ta suy ra hàm số đã cho chỉ có một cực tiểu x = 0
Câu 9:
Ta có: y’ = 3x2 – 6x; y’ = 0 <=> x = 0, x = 2. Các giá trị cực trị của hàm số là:
y1 = y(0) = 1, y2 = y(2) = -3
Vậy tích các giá trị cực trị của hàm số là y1y2 = -3
Câu 10:
Ta có: y’ = 3x2 – 6x, y’ = 0 <=> x = 0, x = 2. Các điểm cực trị của hàm số đã cho là A(0; 2), B(2; -2)
Phương trình đường thẳng AB là
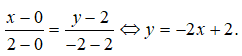
Câu 11:
Ta có: y’ = 3x2 – 12x, y’ = 0 <=> x = 0, x = 4 So sánh các giá trị:
y(-1) = -7, y(0) = 0, y(4) = -32, y(5) = -25
Ta có giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [-1; 5] là 0 và -32.
Câu 12:
Ta có: y’ = 3x2 – 3. Hệ số góc của tiếp tuyến là: k = y'(0) = -3
Phương trình tiếp tuyến là y – 2 = -3(x – 0) <=> y = -3x + 2
Câu 13:
Xét điểm A(x0, y0) thuộc đồ thị hàm số. Phương trình tiếp tuyến d tại A của đồ thị hàm số là
![]()
Tiếp tuyến đi qua M(0;-7) khi và chỉ khi
![]()
Phương trình trên (ẩn x0) có ba nghiệm nên có ba tiếp tuyến thỏa mãn yêu cầu bài toán.
Câu 14:
Ta có: y’ = 3x2 – 6x + 2,
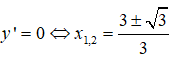
Giá trị cực trị của hàm số là:
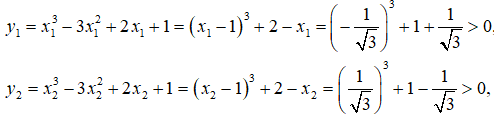
Lập bảng biến thiên ta suy ra đồ thị hàm số cắt trục hoành tại 1 điểm.

