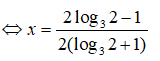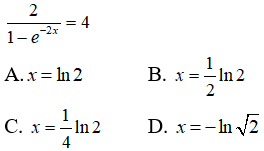
Câu 1: Giải phương trình 10^x = 0,00001

A. x = -log4    B. x = -log5    C. x = -4    D. x = -5

Câu 2: Giải phương trình

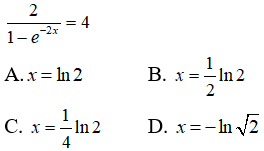
Câu 3: Cho phương trình

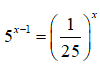
Nghiệm của phương trình này nằm trong khoảng nào dưới đây ?

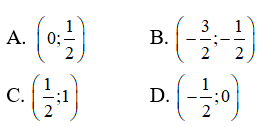
Câu 4: Giải phương trình 3^{2x – 3} = 7 . Viết nghiệm dưới dạng thập phân, làm tròn đến hàng phần nghìn.

A. x = 2,38   B. x = 2,386    C. x = 2,384   D. x = 1,782

Câu 5: Tính tổng bình phương các nghiệm của phương trình 4^{x2 + 2} – 9.2^{x2 + 2} + 8 = 0

A. 2   B. 4   C. 17   D. 65

Câu 6: Giải phương trình 4^x + 2^{x + 1} – 15 = 0. Viết nghiệm tìm được dưới dạng thập phân, làm tròn đến hàng phần trăm

A. x = 0,43     B. x = 0,63    C. x = 1,58    D. x = 2,32

Câu 7: Giả sử x₁, x₂ là hai nghiệm của phương trình 7^x + 2.7^{1 – x} – 9 = 0.

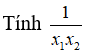
A. log₂7 + 1   B. log₇2 + 1    C. log₇2    D. log₂7

Câu 8: Tìm nghiệm của phương trình 4^{1 – x} = 3^{2x + 1}

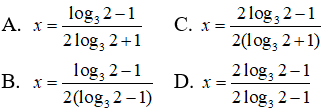
Hướng dẫn giải và Đáp án

1-D

2-B

3-A

4-B

5-A

6-C

7-D

8-C

Câu 1:

10^x = 0,00001 <=> 10^x = 10^-5 <=> x = -5

Câu 2:

PT <=> 1 – e^-2x = 1/2 <=> e^-2x = 1/2 <=> -2x = ln(1/2) = -ln2 <=> x = (1/2)ln2

Câu 3:

PT <=> 5^{x – 1} = 5^-2x <=> x – 1 = -2x <=> 3x = 1 <=> x = 1/3

Câu 4:

3^{2x – 3} = 7 <=> 2x – 3 = log₃7 <=> x = (1/2)(log₃7 + 3) ≈ 2,386

Câu 5:

Đặt t = 2^{x2 + 2}, nhận được t² – 9t + 8 = 0 <=> t = 1 hoặc t = 8

Với t = 1, nhận được 2^{x2 + 2} = 1 (vô nghiệm)

Với t = 8, ta có: 2^{x2 + 2} = 8 = 2³ <=> x² + 2 = 3 <=> x = ± 1

Tổng bình phương các nghiệm: 1² + (-1)² = 2

Câu 6:

Đặt t = 2^x > 0, nhận được phương trình t² + 2t – 15 = 0 <=> t = -5 (loại) hoặc t = 3 hay 2^x = 3 <=> x = log₂3 = ln3/ln2 ≈ 1,58

Câu 7:

Đặt t = 7^x, được phương trình:

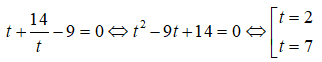
Từ đó tìm được x₁ = 1, x₂ = log₇2. Ta có:

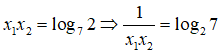
Câu 8:

4^{1 – x} = 3^{2x + 1} <=> 2^{2 – 2x} = 3^{2x + 1}

Lấy lôgarit cơ số 3 hai vế ta được :

(2 – 2x)log₃2 = 2x + 1 <=> 2x(log₃2 + 1) = 2log₃2 – 1

Comments

comments