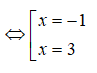
Câu 6: Giải phương trình logx = log(x + 3) – log(x – 1)

A. x = 1   B. x = 3   C. x = 4    D. x = -1, x = 3

Câu 7: Giải phương trình log_√2(x + 1) = log₂(x² + 2) – 1

A. x = 1   B. x = 0   C. x = 0, x = -4   D. x = 0, x = 1

Câu 8: Cho biết log_b2x + log_x2b = 1, b > 0, b ≠ 1, x ≠ 1. Khi đó x bằng:

A. b    B. √b    C. 1/b     D. 1/b²

Câu 9: Cho biết 2^x = 8^{y + 1} và 9^y = 3^{x – 9} . Tính giá trị của x + y

A. 21     B. 18   C. 24    D. 27

Câu 10: Giả sử x, y là hai số thực thỏa mãn đồng thời 3^{x2 – 2xy} = 1 và 2log₃x = log₃(y + 3). Tính x + y

A. 9/4     B. 3/2    C. 3   D. 9

Hướng dẫn giải và Đáp án

Câu 6:

Điều kiện x > 1. Khi đó phương trình tương đương với

logx(x – 1) = log(x + 3) <=> x(x – 1) = x + 3 <=> x² – 2x – 3 = 0

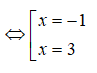
Loại nghiệm x = -1 do không thỏa mãn điều kiện. Phương trình có một nghiệm x = 3.

Chọn đáp án B.

Chú ý: Cũng như ở ví dụ 5, sai lầm học sinh dễ gặp bài này là do chủ quan muốn tiết kiệm thời gian mà quên đặt điều kiện, dẫn tới không loại được nghiệm x = -1 và chọn phương án nhiễu D.

Câu 7:

Điều kiện x > -1. Khi đó phương trình tương đương với

2log₂(x + 1) = log₂(x² + 2)

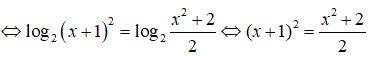
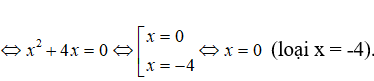
Chọn đáp án B

Câu 8:

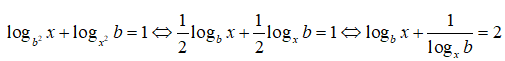
<=> (log_bx – 1)² = 0 <=> log_bx = 1 <=> x = b . Chọn đáp án A.

Chú ý. Khác với các ví dụ trên, các biến đổi trong ví dụ này không làm mở rộng miền xác định của phương trình (x > 0). Do đó ta đã không nhất thiết phải đặt điều kiện x > 0. Trong nhiều trường hợp việc bỏ qua đặt điều kiện sẽ làm đơn giản hơn và tiết kiệm thời gian.

Câu 9:

2^x = 8^{y + 1} => 2^x = 2^{3y + 3} => x = 3y + 3

9^y = 3^{x – 9} => 2y = x – 9

Từ (1) và (2) tìm được x = 21, y = 6. Vậy x + y =27.

Chọn đáp án D.

Câu 10:

Điều kiện x > 0, y > -3. Ta có: 3^{x2 – 2xy} = 1 <=> x² – 2xy = 0 <=> x(x – 2y) = 0 <=> x – 2y = 0 (x > 0) <=> x = 2y (1)

2log₃x = log₃( y + 3) <=> log₃x² = log₃(y + 3) <=> x² = y + 3 (2)

Thế (1) vào (2) ta được

Comments

comments