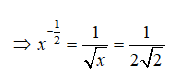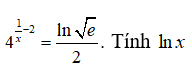
Câu 1: Giả sử x là nghiệm của phương trình

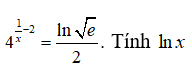
A. 0   B. ln3    C. –ln3    D. 1/ln3

Câu 2: Tính tích tất cả các nghiệm của phương trình 3^{2×2 + 2x + 1} – 28.3^{x2 + x} + 9 = 0

A. -4    B. -2    C. 2    D. 4

Câu 3: Tìm nghiệm của phương trình 2^{x – 1} = 3^{1 – 2x}

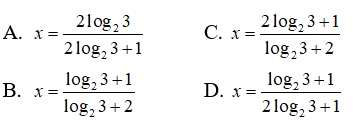
Câu 4: Giải phương trình (x² – 2x)lnx = lnx³

A. x = 1, x = 3    B. x = -1, x = 3     C. x = ±1, x = 3    D. x = 3

Câu 5: Nếu log₇(log₃(log₂x)) = 0 thì x^-1/2 bằng :

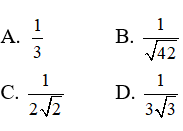
Hướng dẫn giải và Đáp án

1-A

2-B

3-D

4-D

5-C

Câu 1:

Để ý rằng

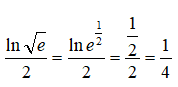
nên phương trình đã cho tương đương với

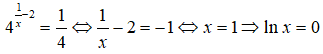
Chọn đáp án A.

Câu 2:

Đặt t = 3^x2 + x > 0 nhận được phương trình

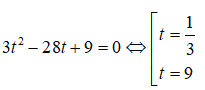
Với t = 1/3 = 3^-1 được 3^{x2 + x} = 3^-1 <=> x² + x + 1 = 0(vô nghiệm)

Với t = 9 được phương trình x² + x – 2 = 0 <=> x -2 hoặc x = 1

Tích của hai nghiệm này bằng -2.

Chọn đáp án B

Câu 3:

Có nhiều cách biến đổi phương trình này. Tuy nhiên, nhận thấy các biểu thức trong các phương án đều chứa log₂3 , nên ta lấy lôgarit cơ số 2 hai vế của phương trình để nhận được (x – 1) = (1 – 2x)log₂3

<=> x(2log₂3 + 1) = log₂3 + 1

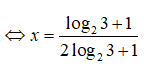
Chọn đáp án D

Câu 4:

Điều kiện x > 0. Khi đó phương trình đã cho tương đương với

(x² -2x)lnx = 3lnx <=> (x² – 2x + 3)lnx = 0

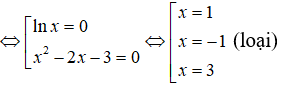
Vậy phương trình có hai nghiệm là x = 1, x = 3 .

Chọn đáp án A.

Chú ý. Sai lầm thường gặp là quên điều kiện dẫn đến không loại được nghiệm x = -1 và chọn phương án nhiễu C.

Thậm chí, có thể học sinh biến đổi (x² – 2x)lnx = 3lnx <=> x² -2x = 3(giản ước cho lnx) dẫn đến mất nghiệm x = 1 và chọn phương án nhiễu D.

Câu 5:

log₇(log₃(log₂x)) = 0 <=> log₃(log₂x) = 7⁰ = 1

<=> log₂x = 3^t <=> x = 2³ = 8

Chọn đáp án C

Comments

comments