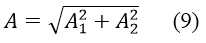
CÂU HỎI
Câu 1 (trang 60 sgk Vật Lí 12 nâng cao): Nêu rõ vai trò của độ lệch pha khi tổng hợp hai dao động điều hòa cùng Phương và cùng tần số góc.
Lời giải:
Độ lệch pha của dao động ∆φ mà biên độ khác ta có:
+ Trường hợp hai dao động là cùng pha khi ∆φ = 2nπ, n là số nguyên.
Biên độ của dao động tổng hợ là lớn nhất A = A1 + A2 (7)
+ Trường hợp ngược pha ∆φ = (2n+1)π
Biên độ của dao động tổng hợp là nhỏ nhất A = |A1 – A2 | (8)
+ Trường hợp là vuông góc pha khi ∆φ = (2n+1)π/2
Biên độ dao động tổng hợp là:
![]()
+ Tổng quát khi độ lệch pha bất kì ta có biên độ dao động tổng hợp như công thức (4).
BÀI TẬP
Bài 1 (trang 60 sgk Vật Lí 12 nâng cao): Xét dao động tổng hợp của 2 dao động hợp thành có cùng tần số. Biên độ của dao động tổng hợp không phụ thuộc.
A. Biên độ dao động hợp thành thứ nhất
B. Biên độ của dao động hợp thành thứ hai
C. Tần số chung của hai pha hợp thành.
D. Độ lệch pha của hai dao động hợp thành.
Lời giải:
Chọn C.
Biên độ của dao động tổng hợp không phụ thuộc tần số chung của hai dao động cơ hợp thành.
Bài 2 (trang 60 sgk Vật Lí 12 nâng cao): Hai dao động cơ học điều hòa cùng phương, cùng tần số góc ω = 50rad/s, có biên độ lần lượt là 100mm và 173mm, dao động thứ hai trễn pha π/2 so với dao động thứ nhất. Xác định dao động tổng hợp.
Lời giải:
Chọn gốc thời gian sao cho pha ban đầu của dao động thứ nhất bằng không, ta có:
x1 = 0,1cos50t (m)
x2 = 0,173cos(50t – π/2) (m)
Các vectơ tương ứng:
x1 < → X1 có độ dài 0,1 m, x2 <-> X2 có độ dài là 0,173m.
Vào thời điểm t = 0, góc (Ox,X1 ) = 0
Góc (Ox,X2→) = π/2 (hình 2.12)
Hai dao động vuông pha nên
A2 = AA12 + A22 = (0,1)2 + (0,173)2 = 0,0(12 + √(32 )) = 0,04
A = 0,2m. góc (Ox,X→) = -π/3.
Vậy x = 0,2cos(50t-π/3) (m)
Bài 3 (trang 60 sgk Vật Lí 12 nâng cao): Dùng công thức lượng giác (tổng của hai cosin) tìm tổng hợp của hai dao động điều hòa cùng Phương, cùng tân số góc ω, cùng biến độ và có độ lệch pha ∆φ. Đổi chiều với kết quả nhận được bằng cách dùng Phương pháp đơn giản đồ Fren – nen.
Lời giải:
Cho hai dao động điều hòa cùng Phương, cùng tần số x1 = Acos(ωt + φ1 ); x2 = Acos(ωt + φ2) có thể tính x = x1 + x2 bằng công thức lượng giác. Áp dụng công thức:
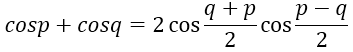
Ta có :

Với ∆φ = φ1 – φ2. Công thức trên chứng tỏ rằng dao động tổng hợp x có cùng tần số góc ω, có biên độ 2Acos(∆φ/2) cào lệch pha (∆φ/2) so với từng dao động x1 hoặc x2. Điều này hoàn toàn phù hợp với Phương pháp Fren – nen.