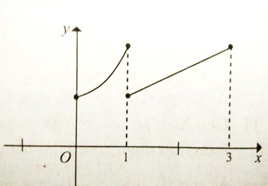
Câu 1: Cho đồ thị hàm số có dạng như hình vẽ.
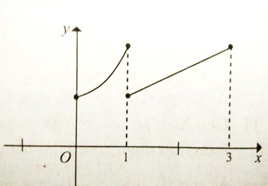
Hàm số đồng biến trên:
A. (0;1)
B. (1;3)
C. (0; 1) ∪ (1; 3)
D. (0;1) và (1;3).
Câu 2: Hỏi hàm số
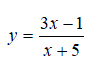
đồng biến trên các khoảng nào?
A. (-∞ ; +∞) B. (-∞; -5)
C. (-5; +∞) ∪ (1; 3) D. (0; 1) và (1; 3)
Câu 3: Tìm khoảng đồng biến của hàm số y = 2x3 – 9x2 + 12x + 3
A.(-∞; 1) ∪ (2; +∞) B. (-∞ 1] và [2; +∞)
C. (-∞; 1) và (2; +∞) D. (1;2)
Câu 4: Khoảng nghịch biến của hàm số y = x4 – 2x2 – 1 là:
A. (-∞; -1) và (0; 1) B. (-∞; 0) và (1; +∞)
C. (-∞; -1) ∪ (0; 1) D. (0;1)
Câu 5: Cho hàm số
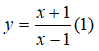
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số (1) nghịch biến trên R\{1}
B. Hàm số (1) nghịch biến trên (-∞; 1) và (1; +∞)
C. Hàm số (1) nghịch biến trên (-∞; 1) ∪ (1; +∞)
D. Hàm số (1) đồng biến trên (-∞; 1) và (1; +∞)
Câu 6: Tìm khoảng đồng biến của hàm số f(x)= x + cos2x
A. R\{0} B. (-∞; +∞) C. (-1; 1) D. (0; π)
Hướng dẫn giải và Đáp án
| 1-D | 2-D | 3-C | 4-A | 5-B | 6-B |
Câu 1:
Trên khoảng (0; 1) đồ thị hàm số đi lên từ trái qua phải
Trên khoảng (1; 3) đồ thị hàm số đi lên từ trái qua phải
Đồ thị hàm số bị gián đoạn tại x = 1. Do đó hàm số đồng biến trên từng khoảng (0; 1) và (1; 3)
Câu 2:
Hàm số xác định ∀x ≠ -5
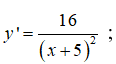
y’ xác định ∀x ≠ -5 . Bảng xét dấu y’:
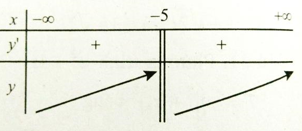
Vậy hàm số đồng biến trên các khoảng (-∞; -5) và (-5; +∞)
Câu 3:
Ta có
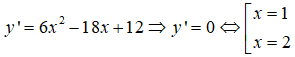
Bảng xét dấu đạo hàm:
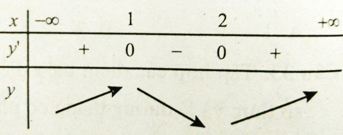
Hàm số đồng biến trên các khoảng (-∞; 1) và (2; +∞)
Câu 4:
Ta có
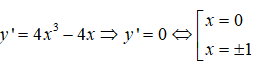
Bảng xét dấu đạo hàm
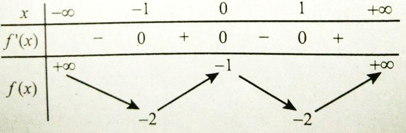
Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1)
Câu 5:
Hàm số
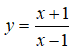
xác định ∀x ≠ 1
Ta có:
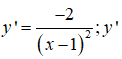
xác định ∀x ≠ 1
Bảng xét dấu đạo hàm
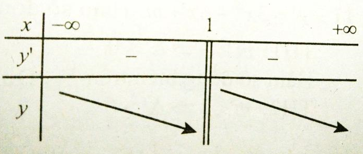
Hàm số nghịch biến trên các khoảng (-∞ 1) và (1; +∞)
Câu 6:
f'(x) = 1 – 2sinxcosx = (sinx – cosx)2 ≥ 0 ∀x ∈ R
Hàm số đồng biến trên khoảng (-∞; +∞)