Câu 6: Cho hàm số y = x⁴ – 2x² + 3 . Kết luận nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng (-∞; -1) ∩ (0; 1)

B. Hàm số đồng biến trên khoảng (-1; 0) ∪ (1; +∞)

C. Hàm số nghịch biến trên khoảng (-∞; -1) ∪ (0; 1)

D. Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞)

Câu 7: Cho hàm số y = sin2x – 2x. Hàm số này

A. Luôn đồng biến trên R     B. Chỉ đồng biến trên khoảng (0; +∞)

C. Chỉ nghịch biến trên (-∞; -1)    D. Luôn nghịch biến trên R

Câu 8: Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1) ?

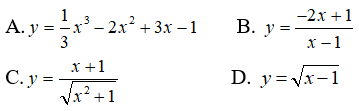
Câu 9: Tìm m để hàm số

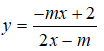
luôn nghịch biến trên khoảng xác định.

A.-2 < m ≤ 2     B. m < -2 hoặc m > 2

C. -2 < m < 2     D. m ≠ ±2

Câu 10: Cho hàm số y = -x³ + 3x² + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)

A. m < 1    B. m ≥ 1    C. m ≤ -1    D. m ≥ -1

Hướng dẫn giải và Đáp án

6-D

7-D

8-C

9-C

10-C

Câu 6:

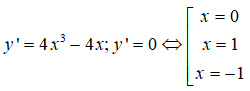
Bảng xét dấu y’:

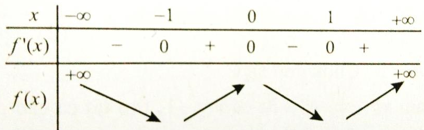
Từ đó ta có: Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞) , nghịch biến trên các khoảng (-∞; -1) và (0; 1) . Chọn đáp án D.

Câu 7:

Tập xác định D = R Vậy hàm số luôn nghịch biến trên R

Chọn đáp án D.

Câu 8:

Hàm số y = x³/3 – 2x² + 3x – 1 có y’= x² – 4x + 3 . Hàm số đồng biến trên các khoảng (-∞; 1) và (3; +∞) .

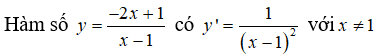
Hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞) .

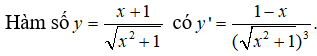
Hàm số đồng biến trên khoảng (-∞;1) và nghịch biến trên khoảng (1; +∞) .

Hàm số đồng biến trên khoảng (1; +∞) .

Chọn đáp án C.

Câu 9:

Tập xác định

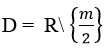
Hàm số nghịch biến trên từng khoảng

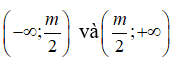
khi và chỉ khi

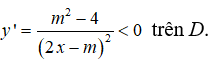
Suy ra -2 < m < 2. Chọn đáp án C.

Câu 10:

Ta có y’ = -3x² + 6x + 3m. Hàm số nghịch biến trên khoảng (0; +∞) nếu y’ ≤ 0 trên khoảng (o; +∞)

Cách 1: Dùng định lí dấu tam thức bậc hai.

Xét phương trình -3x² + 6x + 3m. Ta có Δ’ = 9(1 + m)

TH1: Δ’ ≤ 0 => m ≤ -1. Hàm số nghịch biến trên R .

TH2: Δ’ > 0 => m > -1; y’ = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .

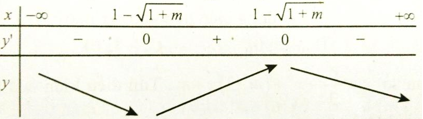
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.

Từ TH1 và TH2, ta có m ≤ -1

Cách 2: Dùng phương pháp biến thiên hàm số.

Ta có y’ = -3x² + 6x + 3m ≤ 0, ∀x > 0 <=> 3m ≤ 3x² – 6x, ∀x > 0

Từ đó suy ra 3m ≤ min(3x² – 6x) với x > 0 Do đó m ≤ -1.

Chọn đáp án C.

Comments

comments